Synopsis

Keywords: Data Analysis, Arterial spin labelling

A Variational Autoencoder (VAE) based framework was created to solve perfusion parameter estimation problem for ASL non-linear forward models. The ultimate goal was to build up an efficient and uncertainty-aware framework for parameter estimation problem in medical imaging, using the concept from Variaitonal Bayes (VB) which was already applied to ASL. Evaluation was performed using simulation and real data experiments with a bi-exponential model and two ASL-MRI forward models with different complexity. Compared with Markov Chain Monte Carlo (MCMC) and analytical VB (aVB), our VAE-based model achieved comparable accuracy, and hundredfold improvement in computational time.

Introduction

Arterial spin labeling (ASL) is a non-invasive magnetic resonance imaging (MRI) technique designed for quantifying tissue perfusion¹. Bayesian inference has been shown useful in ASL perfusion quantification^2,3. Unlike frequentist statistical approaches, Bayesian inference enables parameter estimation process to also estimate the level of confidence. Multiple Bayesian inference algorithms already exist, for example, Laplace approximation⁴, Markov Chain Monte Carlo⁵(MCMC) and analytical Variational Bayes² (aVB) . However, these inference frameworks require multiple iterations resulting in an estimator that scales in computational cost with the complexity of the model. Moreover, the optimization process is "memoryless" -- every time a new data set is received, a completely new optimization needs to be conducted. The development of neural networks provides a possible solution to this by amortizing the computational cost among training process.
In this work, we proposed a Variational autoencoder⁶ (VAE) based neural network to perform uncertainty-aware parameter estimation for a non-linear forward model. We adopted the concept from VB of using an approximate representation of the posterior, and the concept from VAE of using the latent space representation to encode the parameters of forward models. The VAE-based neural network is compared with MCMC and aVB on both toy example and practical examples in ASL perfusion MRI, showing a consistency among different methods and suggesting a more efficient calculation using neural networks.

Methods

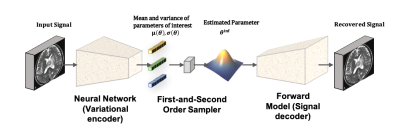
Shown in figure 1, the VAE-like structure contained three parts: a variational encoder, a latent space sampler and a forward model. Unlike conventional VAE⁶, latent variables of VAE-like structure were specified to be particular model parameters and the decoder in our architecture was a generating function, the non-linear model, rather than another neural network. We employed a 50-layer Residual Neural Network⁷ (RNN) as the encoder whose weights were trained using Adam optimizer with initial learning rate = 0.001, β₁ = 0.9 , β₂ = 0.9.
$$Loss = \underbrace{{\rm KL}(q(\theta \mid y)|| p(\theta))}_{\rm (i)~ prior-posterior} + \underbrace{{\rm KL}(P(y)|| P^{\prime}\left(y^{\prime}\right))}_{\rm (ii)~ recovered~signal} + \underbrace{\lambda {\rm RAE}\left(\mu(\theta), \theta^{\rm true}\right)}_{\rm (iii)~ regularization}$$
As loss function, we adopted the sum of a Kullback Leibler (KL) loss between prior and posterior, a KL loss between input and recovered signal and a relative absolute error (RAE) term. The two KL terms were used to explain the uncertainty in estimation from two sources: the physiological variability of parameters and the noise introduced by image acquisition, which can be captured by the prior distribution (i) and data consistency (ii) respectively. We implemented a novel First-and-second order sampler to guarantee the latent samples to be evenly collected from the entire distribution.

Experiments

The framework was evaluated using simulated data from a bi-exponential model, ASL General kinetic model and ASL gamma dispersion model. These models reflected different levels of model complexity and describe common non-linear model fitting scenarios in quantitative MRI. In each case, two hundred thousand datasets were generated as the training data. Gaussian white noises with signal noise ratio (SNR) in [1,1000] were randomly added to 3/4 of them.
Simulation data were generated from bi-exponential example and ASL forward models with amplitude $$$B$$$ and rate $$$a$$$ varying between 0 and 2 for bi-exponential example, perfusion and ATT varying between 0 and 2 ml/g/min and between 0 and 2 seconds for ASL models. Gaussian noise was added to generate data with SNR of infinity, 10, 5 and 2.5. MCMC and aVB were used to estimate parameters from simulation data, to compare the average computational time, the estimated values and the associated uncertainty to that of VAE-base method. To test the practical applications of VAE-based method on ASL data, the in-vivo PCASL dataset with 6 PLDS (0.25, 0.5, 0.75, 1.0, 1.25, 1.5) was considered.

Results

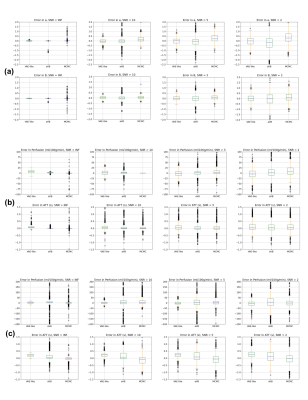
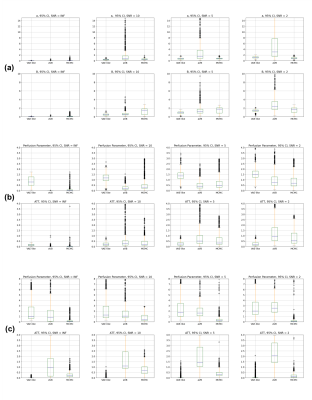
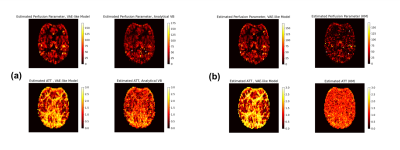
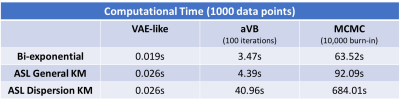
Figure 2 and 3 compare the error and 95% credible interval (CI) of estimations in simulation experiments at different SNR levels. A consistency in estimated values among different inference frameworks can be observed on both bi-exponential example and ASL forward models. Most methods show an increasing CI as SNR decreases, suggesting an expected increasing uncertainty with increase in noise. Figure 4 shows the results from in-vivo experiments, suggesting a similarity between neural network and VB approach. The average computational time is shown in figure 5, indicating a hundredfold to thousandfold improvement by using VAE-based method.

Conclusion and Discussion

In this work, an uncertainty-aware VAE-based framework trained with a new loss function and a novel sampling strategy was proposed to solve parameter estimation problem in the context of medical imaging. Here, ASL kinetic models were used as the examples to test for the feasibility of our idea. A hundredfold improvement was achieved in the computational efficiency without substantial loss of accuracy compared with conventional inference frameworks.

Acknowledgements

This research was supported by Institute of Biomedical Engineering, Department of Engineering Science, University of Oxford. I am grateful to my supervisor Prof Michael Chappell who provided guidance and feedback throughout this project. I am also thankful to Jianqing Zheng for the assistance with coding.