2779
Diffusion Tensor Imaging of tendon and ligament: Influence of crimping behavior and microstructural variations.
Noel Naughton1, Amir Ostadi Moghaddam1, Mariana Kersh1,2,3, Samni Koyejo4, Shreyan Majumdar1, Amy Wagoner Johnson1,2,3,5, and Bruce Damon1,6
1Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Biomedical and Translational Sciences, Carle Illinois College of Medicine, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 4Computer Science Department, Stanford University, Palo Alto, CA, United States, 5Carle R. Woese Institute for Genomic Biology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 6Carle Clinical Imaging Research Program, Stephens Family Clinical Research Institute, Carle Health, Urbana, IL, United States
1Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 2Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Biomedical and Translational Sciences, Carle Illinois College of Medicine, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 4Computer Science Department, Stanford University, Palo Alto, CA, United States, 5Carle R. Woese Institute for Genomic Biology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 6Carle Clinical Imaging Research Program, Stephens Family Clinical Research Institute, Carle Health, Urbana, IL, United States
Synopsis
Keywords: Tendon/Ligament, Diffusion Tensor Imaging
To guide development and optimization of dMRI protocols, here we present a numerical simulation framework for analyzing how changes in collagen microstructure influence the measured diffusion tensor. We experimentally characterize a porcine digital flexor tendon using second harmonic generation (SHG) microscopy to identify characteristic geometric parameters and use these parameter ranges to perform a sensitivity analysis of what microstructural features most influence diffusion tensor imaging (DTI) metrics. We conclude by exploring how geometric changes in collagen crimping due to tissue strain influence DTI metrics.Introduction
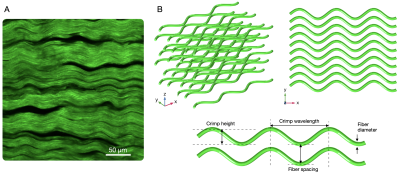
Tendons and ligaments are regularly subjected to large mechanical stresses during use. Understanding the mechanical properties of these tissues is thus crucial to elucidating their functional roles in vivo. A key determinant of these tissue’s mechanical properties is the microstructural organization of the collagen fibers that comprise most of the tissue [1]. These fibers have a hierarchical organization with spatial and temporal heterogeneity that remodels in response to disease and injury [2]. In particular, collagen fibers in tendon and ligament exhibit crimping, which is oscillation along the fiber’s primary axis (Fig. 1). Crimping is believed to play a key role in mediating the mechanical properties of both tendon and ligament with its crimp decreasing as the tissue is stretched during loading [3]. In vivo characterization of this collagen microstructure, and crimp in particular, holds the potential to reveal clinically-relevant biomarkers for developing improved diagnosis methods, targeted rehabilitation treatments, and personalized monitoring of several musculoskeletal disease and injury conditions.Diffusion-weighted MRI (dMRI) is sensitive to changes in tissue microstructure [4], however, its use in collagenous tissues has been limited due to collagenous tissues’ characteristically low T2 values. To guide development and optimization of dMRI protocols, here we present a numerical simulation framework for analyzing how changes in collagen microstructure influence the measured diffusion tensor. We experimentally characterize a porcine digital flexor tendon using second harmonic generation (SHG) microscopy to identify characteristic geometric parameters and use these parameter ranges to perform a sensitivity analysis of what microstructural features most influence diffusion tensor imaging (DTI) metrics. We conclude by exploring how geometric changes in collagen crimping due to tissue strain influence DTI metrics.
Methods
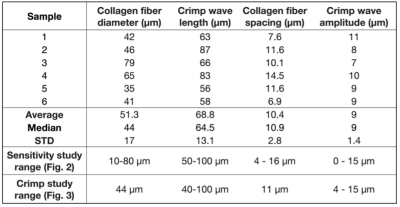
Pig feet were acquired from a local grocer, and the digital flexor tendons were harvested. SHG images (Fig. 1a) were captured using the methods described in [5a]. Six ROIs were sampled from the images and Fiji was used to measure four microstructural features: collagen fiber diameter, interstitial spacing between fibers, crimp wave amplitude and crimp wavelength.To understand how collagen microstructure features influence the DTI signal, we numerically simulate a dMRI experiment using the lattice Boltzmann method (LBM) [6]. We define a three-dimensional biphasic domain consisting of collagen fibers and interstitial water and parameterized by the same four parameters measured from the SHG images. Collagen fibers are packed in a square lattice with crimp modeled as an oscillating sine wave in the fiber direction (Fig 1b). We define a unit cell of the domain which we simulate with periodic boundary conditions on all sides. Numerical parameters were chosen so at least 40 nodes spanned the unit cell cross-section with the time step chosen based on the defined node spacing and an LBM optimization procedure.
DTI scans were simulated using a PGSE sequence with 12 directions and typical sequence parameters for musculoskeletal DTI (gradient duration of 12.5 ms, gradient spacing of 25.6 ms, and a b-value of 440 s/mm2). For each sequence, a non-diffusion weighted simulation was also performed and the diffusion tensor was computed using custom Python code. Eigenvalues and fractional anisotropy (FA) were computed for each diffusion tensor. Noise was not considered.
Results
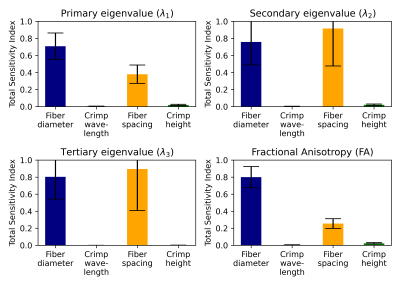
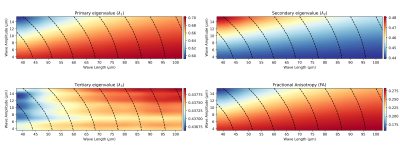
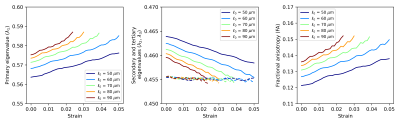
Table 1 reports the microstructural parameters from the SHG and the parameters used in the numerical simulation studies. Figure 2 reports the results of a sensitivity study of how different variations in microstructural parameters influence eigenvalues and FA, based on the methods reported in [7]. Diameter and fiber spacing exhibit the most influence on the DTI metrics, with the crimp amplitude exhibiting slight influence and the crimp wavelength having almost no influence on the DTI metrics. These results suggest that variability in the diameter and fiber spacing dominate. However, for a tendon undergoing deformation, these two parameters are expected to be relatively constant while the crimp wavelength and amplitude change.To explore this effect, we fixed the fiber diameter and spacing to the median value measured in Table 1 and spanned a range of crimp amplitudes and wavelengths (Fig. 3). If collagen elasticity is ignored, a deforming fiber will reduce its level of crimp during stretching while maintaining a constant fiber length. If this stretch is proportional to the change in the crimp wavelength, then the crimp amplitude can be computed. Figure 4 considers how a fiber deforming in this way will influence the DTI metrics. Changes in λ1 and FA are observed while λ2 has only a slight change and λ3 is insensitive to the change.
Discussion and Conclusion
Measuring the microstructure of collagen is technically challenging. Overall, our results facilitate the design of dMRI sequences that accurately capture the microstructural properties of the tissue. The approach described here provides a framework for optimization of dMRI sequence parameters to maximize microstructural sensitivity as well as development of new post-processing methods to extract additional insight into microstructural organization in collagenous tissues such as ligaments and tendons. Future directions will look at model-free reconstruction methods and q-t imaging paradigms to extract additional microstructural information while considering the impact of SNR and T2-effects.Acknowledgements
Partial funding for this work was provided by NIH/NIAMS (National Institute of Arthritis and Musculoskeletal and Skin Diseases), R01 AR073831.References
[1] Fratzl, Peter. "Collagen: structure and mechanics, an introduction." In Collagen, pp. 1-13. Springer, Boston, MA, 2008.
[2] Sandhu, Simarpreet V., Shruti Gupta, Himanta Bansal, and Kartesh Singla. "Collagen in health and disease." Journal of Orofacial research (2012): 153-159.
[3] Hansen, Kristi A., Jeffrey A. Weiss, and Jennifer K. Barton. "Recruitment of tendon crimp with applied tensile strain." J. Biomech. Eng. 124, no. 1 (2002): 72-77.
[4] Wengler, Kenneth, Takeshi Fukuda, Dharmesh Tank, David E. Komatsu, Megan Paulus, Mingqian Huang, Elaine S. Gould, Mark E. Schweitzer, and Xiang He. "In vivo evaluation of human patellar tendon microstructure and microcirculation with diffusion MRI." Journal of Magnetic Resonance Imaging 51, no. 3 (2020): 780-790.
[5] Moghaddam, A. Ostadi, Z. Lin, M. Sivaguru, H. Phillips, B. L. McFarlin, K. C. Toussaint, and AJ Wagoner Johnson. "Heterogeneous microstructural changes of the cervix influence cervical funneling." Acta Biomaterialia 140 (2022): 434-445.
[6] Naughton, Noel M., Caroline G. Tennyson, and John G. Georgiadis. "Lattice Boltzmann method for simulation of diffusion magnetic resonance imaging physics in multiphase tissue models." Physical Review E 102, no. 4 (2020): 043305.
[7] Naughton, Noel M., and John G. Georgiadis. "Global sensitivity analysis of skeletal muscle dMRI metrics: Effects of microstructural and pulse parameters." Magnetic Resonance in Medicine 83, no. 4 (2020): 1458-1470.
Figures
Figure 1: (a) SHG image of porcine digital flexor tendon. (b) Representation of three-dimensional collagen tissue model used for numerical simulation. The domain is parameterized with the four geometrical parameters labeled. Free water is modeled with a diffusion coefficient of 2 μm2/ms and a relative water content of 1.0. The collagen fiber is modeled with a diffusion coefficient of 0.5 μm2/ms and a relative water content of 0.5. A water impermeable membrane surrounds each collagen fiber.
Table 1: Measurements of microstructural parameters from the SHG image in Figure 1a and the parameter ranges used for the sensitivity study and the crimp variation studies in Figure 2 and Figures 3 and 4, respectively.
Figure 2: Sensitivity results for influence of microstructure parameters on DTI metrics. This study utilized a Sobol method, which is a global sensitivity measurement that decomposes how the variance of the input (microstructure) influences the variance of the output (DTI metrics). Results reported are total sensitivity (out of 1.0) which considers both the role of the parameter individually and its non-linear interactions with other parameters, allowing the sum of scores to be greater than 1.0.
Figure 3: Map of how changes in crimping parameters influence DTI metrics (for constant diameter and fiber spacing). Black dashed lines are contours of constant tendon length, so the DTI metrics of a geometrically deforming fiber with no collagen stretch would travel along a contour.
Figure 4: Expected changes in DTI metrics for strain levels of up to 5% for different initial wavelengths. Results that end before 5% strain are for fibers that become fully stretched, so wave amplitude is zero and thus the fiber cannot deform more without elastic stretch.
DOI: https://doi.org/10.58530/2023/2779