Synopsis

Keywords: Arterial spin labelling, Arterial spin labelling

4D combined angiography and perfusion using radial imaging and arterial spin labelling (CAPRIA) allows dynamic angiograms to be reconstructed. However, the current approach uses a relatively long temporal window to ensure sufficient k-space coverage within each frame, resulting in abrupt changes between adjacent frames, and additional artefacts. In this work, we use a kinetic model of the angiographic signal to constrain the reconstruction of highly undersampled data. A subspace reconstruction was developed for compressed representation of signal during reconstruction for computational efficiency. In-vivo results showed smoother variation of the angiographic signal in the temporal dimension compared to the original approach.

Introduction

Visualization of blood flow through the vessels in the brain provides useful information for diagnosing various cerebrovascular diseases. 4D combined angiography and perfusion using radial imaging and ASL (CAPRIA)^1,2 provides a framework for non-invasively imaging the dynamic process of blood flowing from the neck to the tissue. However, currently 4D CAPRIA only supports angiographic reconstruction using a large number of consecutive TRs to achieve sufficient sampling density in k-space, which, in turn, limits the accurate estimation of blood flow rate which requires temporal resolution around 50ms ³. Moreover, as the blood flows through the vessels, it will undergo inversion recovery, resulting in artefacts caused by signal variation. Therefore, we aim to reconstruct dynamic images at high temporal resolution (15 ms). However, two major obstacles hindered the successful reconstruction in the original CAPRIA framework. Firstly, the number of k-space samples is too small to achieve high quality images with standard reconstruction algorithms at such high temporal resolution (undersampling factor ~1000). Secondly, reconstructing more than 100 3D frames simultaneously makes this task computationally prohibitive. In this work, we introduce a kinetic model of angiography into the reconstruction as additional prior and applied a subspace method to greatly reduce the computational cost.

Methods

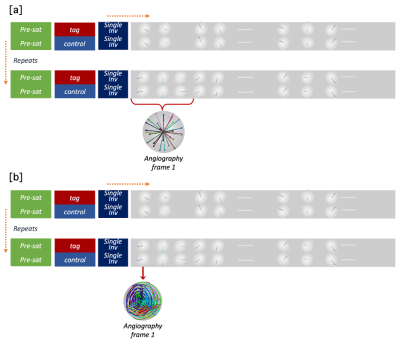
CAPRIA sequence
Here we use the same acquisition method as 4D CAPRIA, except the original radial sampling is replaced with cone sampling⁴. As illustrated in Fig.1, the sequence consists of repetitions of PCASL tag and control modules. Each tag or control module is followed by a series of readouts. However, two changes were made to CAPRIA to facilitate the kinetic model-based subspace reconstruction: rather than using several adjacent readouts (combined across repeats) to reconstruct each frame, here we use only a single readout per frame from each repeat. Though the number of spokes acquired for each frame is greatly decreased, radial sampling is replaced with a cone trajectory to partially compensate for the reduced k-space coverage.
Kinetic model of angiography
The angiographic signal variations across time after labeling can be modeled (2,5), taking into account both the physiological parameters and the pulse sequence settings:
$$S(r_i,t)=A(r_i) \int_{t-\delta t-\tau}^{t-\delta t}D(r_i,t_d)T(\delta_t,t_d)R(t,\delta_t,t_d)\,dt_d$$
Where $$$A(r_i)$$$ is a signal scaling $$$D(r_i,t_d)$$$ is the bolus dispersion, $$$T(\delta_t,t_d)$$$ is the $$$T_1$$$ decay and $$$R(t,\delta_t,t_d)$$$ represents the effects of RF excitation pulses.
Subspace generation
The signal shape of the angiographic model is decided by a few parameters $$$\delta_t, p, s$$$, which are properties of the blood vessels within each voxel (the scaling factor A can be ignored here) . Based on a subspace model^6,7 , reconstruction of the signal across all temporal points could be transformed to the estimation of a few coefficient maps, if the signal is sufficiently compressible.
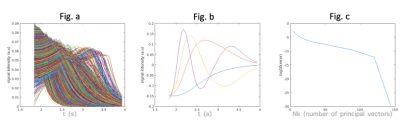
A data matrix $$$X$$$ is formed by randomly drawing $$$N_s$$$ samples from the parameter space. The principal vectors $$$V\{\vec{v_1},\vec{v_2},...,\vec{v_n}\}$$$ are then computed by performing SVD on $$$X$$$ ($$$X=USV^T$$$). Truncation of the first $$$N_k$$$ principal vectors from $$$V$$$ generates a subspace which could offer an approximate representation of the actual signal variations.
Precomputation, LLR reconstruction
The forward model is defined as\begin{equation}\begin{split}y&=PFCx\\&=PFCB\alpha\\&=A\alpha \end{split}\end{equation}where $$$\alpha$$$ are the coefficient maps to be estimated. The computation order of $$$FC$$$ and $$$B$$$ are exchanged for efficiency. A locally low rank constraint is applied on coefficient maps² to leverage the similarity of signals within a local neighbourhood.

Results and discussion

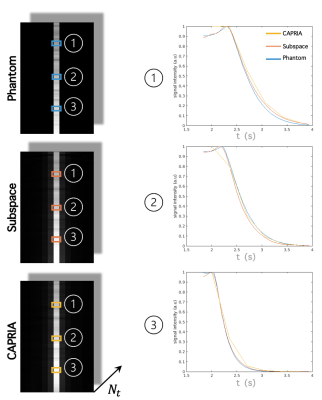
Simulation
Histograms of parameter maps derived from kinetic model fits to previous in vivo CAPRIA data² were calculated, from which we drew samples for constructing the data matrix . We also drew samples to construct a single line numerical phantom ( voxels, 144 timepoints). As shown in Fig. 2, 4 principal components were used for reconstruction of the single line phantom. We compared results from our proposed subspace reconstruction with those from the original (low temporal resolution) CAPRIA reconstruction, with locally low rank constraints applied in both cases. The subspace reconstruction generated results with better fit to the signal evolution across time whilst achieving similar image quality within each volume (Fig 3). The simulation results demonstrates the feasibility of using a subspace reconstruction with small number of principal vectors without loss of accuracy within each volume.
In-vivo reconstruction
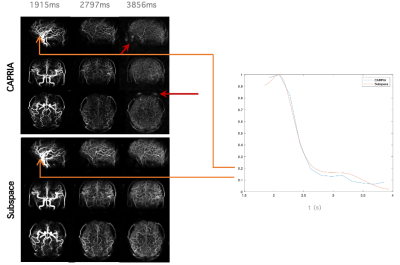
In-vivo data acquired using the cones-CAPRIA framework described above were reconstructed using a subspace model and compared to the previous reconstruction approach (Fig 5). The subspace approach results in high quality reconstructions despite the very large undersampling factor within each frame, albeit with a slight loss of spatial resolution, but a smoother signal variation across time. Although it is expected that a greater number of principal components might represent the signal with higher accuracy, the memory overheads and computation time prohibits us from using more than 4 components at the present time.

Conclusion

Reconstructing high temporal resolution angiograms would make estimation of blood flow rate feasible from 4D CAPRIA data. Incorporating the kinetic model provides an additional prior to compensate for the lack of coverage of k-space at each TR. Subspace reconstruction provides a promising method to reduce computational requirements by only estimating few coefficient maps. Although the intrinsic complexity of the angiography signal makes it less compressible than a T1 recovery signal⁷ , the subspace reconstruction still generated reasonable results with a limited number of principal components.

Acknowledgements

No acknowledgement found.