2748
Multiparameter estimation from DANTE-prepared multi-delay ASL using artificial neural network1Department of Radiological Technology, Faculty of medical sciences, Kyoto College of Medical Science, Nantan, Japan, 2Department of Medical Image Sciences, Faculty of Life Sciences, Kumamoto University, Kumamoto, Japan, 3GE Healthcare, Hino, Japan, 4Radiological center, University of Fukui Hospital, Eiheiji, Japan, 5Faculty of Medical Sciences, University of Fukui, Eiheiji, Japan, 6Radiology section, National Health Insurance Echizen-cho Ota Hospital, Unyu, Japan, 7Department of Radiology, Faculty of Medical Sciences, University of Fukui, Eiheiji, Japan
Synopsis
Keywords: Arterial spin labelling, Arterial spin labelling
A simulation-based supervised neural network was developed for simple and robust parameter estimation from multi-delay DANTE-prepared arterial spin labeling (ASL). The network was trained using 15 million simulation data points. Accuracy and precision were compared between the proposed and conventional methods. The neural-network-based estimation presented higher accuracy and precision than the conventional method that used table lookup. A higher noise immunity was also observed with the proposed method. A simulation-based supervised neural network simplifies the estimation process of multiparametric ASL. The estimation performance of cerebral blood flow and arterial cerebral blood volume was particularly improved by the proposed method.Introduction
Multi-delay arterial spin labeling (ASL) MRI uses multiple post-labeling delays to capture the hemodynamics-induced ASL signal changes, enabling quantification of cerebral blood flow (CBF) and arterial transit time (ATT)1,2. Various preparation pulses are embedded into ASL-MRI to separate the vascular and tissue compartments3-8. The combination of multi-delay acquisition and preparation pulses provides additional hemodynamic parameters. Delays alternating with nutation for tailored excitation (DANTE) pulse-prepared multi-delay ASL can quantify arterial cerebral blood volume (CBVa)8. Although multi-parameterization can enhance the value of ASL, complicated processing techniques are required for multiparameter estimation5,6,8. A previous study reported that simulation-based supervised neural networks improve the accuracy and precision of CBF and ATT estimations9. We hypothesized that this technique can solve the problems associated with multiparameter estimation. Therefore, this study aimed to develop a simulation-based supervised neural network that simply estimates multiple parameters from DANTE-prepared multi-delay ASL signals.Methods
[ASL acquisition] Eight ASL volumes were acquired by two series of multi-delay ASL scans with and without DANTE8.[Simulation data] Simulation data were computed using the two-compartment model8. The ground truths were set as follows: 0–90 (mL/100 g/min), 200–2000 (ms), -4000 (ms), and 0.2–2.4 (mL/100 g) for CBF, ATT, tissue transit time (TTT), and CBVa, respectively. Rician noise was added with 51 levels of standard deviation (0–0.5%M0 at 0.05% intervals). Under these conditions, 15,300,000, 102,000, and 510,000 points were sampled for the training, validation, and test datasets, respectively.
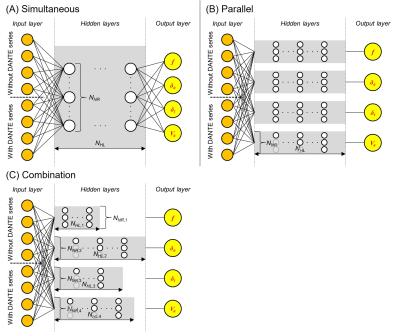
[Neural network] We implemented three network designs (Figure 1). The simultaneous network simultaneously predicts CBF, ATT, TTT, and CBVa using a single network. The parallel network predicts the four parameters simultaneously using subnetworks dedicated to each parameter. The combination network combines four individually optimized networks. Moreover, two loss functions (mean squared error and mean absolute error) were evaluated. The number of hidden layers and neurons in each layer was preliminarily defined using a grid search. Accuracy and precision were assessed on the test dataset using three metrics. Accuracy was assessed using normalized mean absolute error (NMAE) and normalized root mean squared error (NRMSE). Precision was evaluated using the normalized coefficient of variation over repeated training (CVNet) 9,10.
[Table lookup method] A table lookup method (LUT) was devised8. This method estimates the initial ATT and TTT using a signal-weighted delay method1 and the initial CBF using a least-squares solution2. Based on these initial values, lookup tables were computed with predefined ranges for ATT, TTT, and CBF. These parameters are estimated by collating the observed signals from a voxel-by-voxel lookup table.
[Comparison] The selected neural network (NN) and LUT were compared using the test dataset and volunteer images (n = 10; 3.0 T MRI, Discovery MR 750, GE Healthcare, USA). Artificial Rician noise was added to the in vivo images at five levels of standard deviation (0.05, 0.10, 0.15, 0.20, and 0.25%M0). For the test dataset, NMAE and NRMSE were compared between NN and LUT. For in vivo data, the relative change in each parameter value was evaluated for whole gray matter.
Results
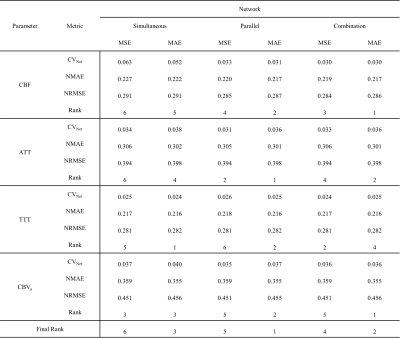
Table 1 presents the results of the network design comparisons. Among the six networks, the parallel network (five hidden layers with 512 neurons) with the mean absolute error loss function exhibited the highest performance owing to the lowest summed ranking.Figure 2 shows the results of the NMAE and NRMSE between the NN and LUT using the test dataset. All parameters derived from the NN indicate lower NMAE and NRMSE values than those derived from the LUT. In particular, CBF and CBVa presented substantially higher accuracies with the NN than with the LUT.
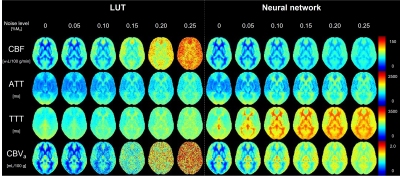
Figure 3 shows the averaged parameter maps across all subjects using the LUT and NN. Higher noise immunity was observed with the NN than with the LUT, particularly with the CBF and CBVa maps.
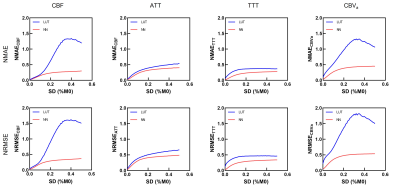
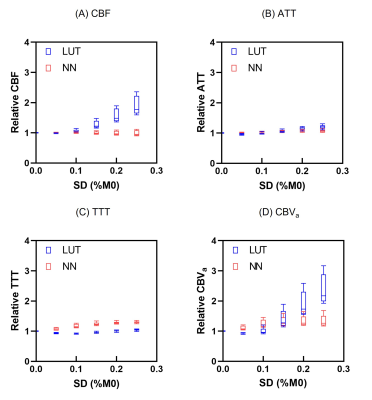
Figure 4 presents the relative changes in CBF, ATT, TTT, and CBVa with respect to noise level. These results are consistent with the visual impression of the parameter maps.
Discussion
The use of two separate networks optimized for single-parameter prediction was recommended for CBF and ATT estimations in a previous study9. In contrast, the parallel network exhibited the highest performance in this study. This difference may be due to the kinetic models and the ASL bolus design. While the previous study estimated CBF and ATT using a single-compartment model, this study estimated the four parameters using a simplified two-compartment model. An optimized network for both the kinetic model and ASL bolus design may be required.Although the measurement results and visual impressions were consistent in CBF and CBVa, a discrepancy existed in ATT and TTT. The NN had lower NMAE and NRMSE values than the LUT. However, the visual impression and measurement of relative change were not different between the NN and LUT for ATT and TTT. The reason for this cannot be strictly determined, but further studies are required to clarify this discrepancy. Nevertheless, the NN improved the performance of the multiparameter estimation from the DANTE-prepared multi-delay ASL.
Conclusion
A simulation-based supervised neural network simplifies the estimation process of multiparametric ASL. Moreover, the estimation performances of CBF and CBVa were significantly improved by the proposed method.Acknowledgements
This work was supported in part by JSPS KAKENHI (grantnumber 21K15802 and 21K07616).References
1. Dai W, Robson PM, Shankaranarayanan A, Alsop DC. Reduced resolution transit delay prescan for quantitative continuous arterial spin labeling perfusion imaging. Magn Reson Med. 2012;67:1252-1265.
2. Ishida S, Kimura H, Isozaki M, et al. Robust arterial transit time and cerebral blood flow estimation using combined acquisition of Hadamard-encoded multi-delay and long-labeled long-delay pseudo-continuous arterial spin labeling: a simulation and in vivo study. NMR Biomed. 2020;33:e4319.
3. Liu P, Uh J, Lu H. Determination of spin compartment in arterial spin labeling MRI. Magn Reson Med. 2011;65:120-127.
4. Matsuda T, Kimura H, Kabasawa H, Kanamoto M. Three-dimensional arterial spin labeling imaging with a DANTE preparation pulse. Magn Reson Imaging. 2018;49:131-137.
5. Shao X, Ma SJ, Casey M, D'Orazio L, Ringman JM, Wang DJJ. Mapping water exchange across the blood-brain barrier using 3D diffusion-prepared arterial spin labeled perfusion MRI. Magn Reson Med. 2019;81:3065-3079.
6. Ohene Y, Harrison IF, Nahavandi P, et al. Non-invasive MRI of brain clearance pathways using multiple echo time arterial spin labelling: an aquaporin-4 study. Neuroimage. 2019;188:515-523.
7. Fujiwara Y, Kimura H, Ishida S, et al. Intravascular signal suppression and microvascular signal mapping using delays alternating with nutation for tailored excitation (DANTE) pulse for arterial spin labeling perfusion imaging. MAGMA. 2020;33:367-376.
8. Ishida S, Kimura H, Takei N, et al. Separating spin compartments in arterial spin labeling using delays alternating with nutation for tailored excitation (DANTE) pulse: A validation study using T2 -relaxometry and application to arterial cerebral blood volume imaging. Magn Reson Med. 2022;87:1329-1345.
9. Ishida S, Isozaki M, Fujiwara Y, et al. Estimation of Cerebral Blood Flow and Arterial Transit Time From Multi-Delay Arterial Spin Labeling MRI Using a Simulation-Based Supervised Deep Neural Network. J Magn Reson Imaging. 2022, in press.
10. Kaandorp MPT, Barbieri S, Klaassen R, et al. Improved unsupervised physics-informed deep learning for intravoxel incoherent motion modeling and evaluation in pancreatic cancer patients. Magn Reson Med. 2021;86:2250-2265.
Figures