2668
Exploring Tensor Decomposition as an Alternative to ICA for Denoising Multi-Echo fMRI data
Eneko Uruñuela1, Miguel Ánguel Veganzones2, and César Caballero-Gaudes1
1Basque Center on Cognition, Brain and Language, Donostia - San Sebastián, Spain, 2University of Deusto, Donostia - San Sebastián, Spain
1Basque Center on Cognition, Brain and Language, Donostia - San Sebastián, Spain, 2University of Deusto, Donostia - San Sebastián, Spain
Synopsis
Keywords: Brain Connectivity, fMRI, Tensor Decomposition
Denoising of the blood oxygen level-dependent signal is critical for the study of brain dynamics with functional MRI data. However, disentangling neurobiological signals from non-neurobiological ones such as head motion-related artifacts, and cardiac-related and respiration-related fluctuations. Multi-echo ICA approaches are often used to denoise the data by exploiting the echo-time dependence of the BOLD signal. Nevertheless, these rely on the optimally combined data and do not employ the information contained in the different echo-time signals. Here, we explore the potential of tensor decomposition techniques, which can simultaneously consider all the information available, as a way to process multi-echo fMRI data.Introduction
Denoising the blood oxygen level-dependent (BOLD) signal is central for studying brain organization and dynamics with functional MRI (fMRI) data. Nevertheless, structured noise from head motion, cardiac-related brain pulsations, hardware artifacts, and respiratory variations can considerably corrupt fMRI signal dynamics, making the distinction of neurobiological signals difficult1,2. Multi-echo (ME) fMRI techniques are a promising resource to discern neuronal signals based on the signal decay properties and have been shown to be excellent at removing spatially focal artifacts (e.g. due to motion)1,3,4. Typically, ME-ICA techniques have been employed to denoise the data by exploiting the time-echo (TE) dependence of the BOLD signal, showing improved mapping of task-induced activation5, denoising of resting-state fMRI data, and deconvolution of changes in the neuronal-related signal6. However, ME-ICA approaches decompose the optimally combined data (operating in 2D) and omit the valuable information contained in the different echo signals. Here, we explore the potential of tensor decomposition approaches, which simultaneously consider all the information contained by the different TEs, as a way to process multi-echo fMRI data.Theory and Methods
We construct a tensor $$$\mathbf{X} \in \mathbb{R}^{T, S, E}$$$ by stacking the multi-echo data, where $$$T$$$ is the number of TRs, $$$S$$$ is the number of voxels and $$$E$$$ is the number of TEs. Thus, for a given rank (or the number of components) $$$k$$$, the tensor can be decomposed via canonical polyadic decomposition7 into spatial, temporal, and TE components (Figure 1A) by means of the alternating least squares technique (ALS, Figure 1B). As a proof of concept, we solve the ALS problem with $$$k=7,10,16,32$$$ on a motor task and resting-state fMRI data acquired in a healthy subject that was scanned on a 3T Siemens Prisma with the following parameters: 340 scans,TR=1.5 s,TEs =10.6/28.69/46.78/64.87/82.96ms,FA=70°,multiband=4,GRAPPA=2, 52 slices (interleaved),Partial Fourier=6/8,FoV=211×211mm2,voxel=2.4×2.4×3mm3. Motor task conditions: left and right-hand finger tapping, moving the left and right-foot toes, and moving the tongue. Data processing was performed using AFNI,8 FSL,9 and ANTS,10 including multi-echo T2*-weighted combination, nuisance regression of up to fourth-order Legendre polynomials, parameter realignment, and temporal derivatives, smoothing of 4mm FWHM, and conversion to percent signal change. We compare the tensor decomposition approach with ME-ICA implemented in tedana in terms of its denoising performance and characterization of functional connectivity patterns using seed voxel correlation (Instacorr in AFNI, 3mm radius). Note that the denoised (reconstructed) data in the tensor decomposition approach is equal to the sum of the weighted good components.Results
Figure 2 shows the correlation across components found via tensor decomposition in their temporal, spatial, and TE signatures for a rank $$$k=7,10,16,32$$$. Importantly, the tensor decomposition of both the motor task and resting-state data illustrates that the range of the rank at which it yields reasonable results is narrower and considerably lower than the number of components typically seen on ME-ICA, since nearly all components are highly collinear in their temporal and TE signatures at ranks between 7 and 32. Here, ranks 10 and 16 produce pairs of components that are not correlated with each other, making a better differentiation of components possible. Figure 3 depicts the spatial (z-scored) and temporal signatures for a rank of 10 decomposition of the motor task data. Components 1-5 show clear artifacts that are highly correlated with each other. On the other hand, component 6 can be clearly related to the motor task, but its timecourse is highly correlated with that of component 9, which shows high-frequency fluctuations commonly associated with cardiac pulsations in addition to the prominent BOLD signal changes induced by the task. Component 10 also shows a clear cardiac component, while component 8 illustrates slow fluctuations and drifts mostly present on the edges of the brain, probably related to head and respiratory-related motion. Decomposition performed on the resting-state data (Figure 4) shows three artifactual components (2,3,10). A cardiac-related artifact is observed in component 9, whose temporal signature shows high frequency, and major arteries and draining veins delineated in its spatial signature. Components 5,6,8 show plausible resting-state spatio-temporal patterns. Components 1,4,7 include a mixture of artefactual signals, vascular pulsatility effects, and possible neuronally-driven patterns of BOLD activity in sensorimotor (1), fronto-parietal and precuneus (4), and bilateral parietal (7) regions. Figure 5 compares the tensor decomposition and ME-ICA (tedana) approaches. Compared to the optimally combined data, tedana tracked the preprocessed signal more accurately across the brain. Besides, functional connectivity maps obtained with the denoised tensor decomposition data yielded much higher correlation values than those obtained with tedana. This higher correlation across large parts of the brain is expected since the denoised signal is the weighted sum of a few (accepted) tensor components.Conclusions
While our results show that using the information given by the different echos in a tensor is promising to improve the denoising of multi-echo data, tensor decomposition approaches are challenging. The choice of the tensor order is critical to interpret and obtain stable the tensor components. However, to obtain plausible components, the number of components must be considerably lower than with ME-ICA. Morover, the tensor components offer a new, complementary view of the sources of the fMRI data, which calls for new criteria for their classification and interpretation in terms of BOLD-related, physiological, and artifactual sources.Acknowledgements
This research was funded by the Spanish Ministry of Economy and Competitiveness (RYC-2017- 415 21845), the Basque Government (BERC 2018-2021, PIB 2019 104, PRE_2020_2_0227), and the Spanish 416 Ministry of Science, Innovation and Universities (PID2019-105520GB-100).References
- Power, J. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini, P. A., & Martin, A. (2018). Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proceedings of the National Academy of Sciences, 115(9), E2105-E2114.
- Caballero-Gaudes, C., & Reynolds, R. C. (2017). Methods for cleaning the BOLD fMRI signal. Neuroimage, 154, 128-149.
- Kundu, P., Inati, S. J., Evans, J. W., Luh, W. M., & Bandettini, P. A. (2012). Differentiating BOLD and non-BOLD signals in fMRI time series using multi-echo EPI. Neuroimage, 60(3), 1759-1770.
- Lynch, C. J., Elbau, I., & Liston, C. (2021). Improving precision functional mapping routines with multi-echo fMRI. Current Opinion in Behavioral Sciences, 40, 113-119.
- Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson, M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015). Tracking ongoing cognition in individuals using brief, whole-brain functional connectivity patterns. Proceedings of the National Academy of Sciences, 112(28), 8762-8767.
- Caballero-Gaudes, C., Moia, S., Panwar, P., Bandettini, P. A., & Gonzalez-Castillo, J. (2019). A deconvolution algorithm for multi-echo functional MRI: Multi-echo Sparse Paradigm Free Mapping. Neuroimage, 202, 116081.
- Comon, P., Luciani, X., & De Almeida, A. L. (2009). Tensor decompositions, alternating least squares and other tales. Journal of Chemometrics: A Journal of the Chemometrics Society, 23(7-8), 393-405.
- Cox, R. W. (1996). AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical research, 29(3), 162-173.
- Jenkinson, M., Beckmann, C. F., Behrens, T. E., Woolrich, M. W., & Smith, S. M. (2012). Fsl. Neuroimage, 62(2), 782-790.
- Tustison, N. J., Cook, P. A., Klein, A., Song, G., Das, S. R., Duda, J. T., ... & Avants, B. B. (2014). Large-scale evaluation of ANTs and FreeSurfer cortical thickness measurements. Neuroimage, 99, 166-179.
Figures
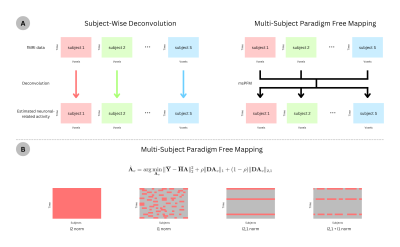
A) Illustration of the decomposition of a tensor into temporal (T), spatial (S), and echo-time (E) components and a diagonal vector of weights (λ) B) Steps of the alternating least squares algorithm.
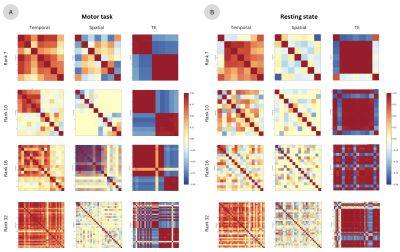
Correlation between temporal, spatial, and echo-time components of the motor task for a decomposition of rank 7, 10, 16, and 32. B) Correlation between temporal, spatial, and echo-time components of the resting-state data for a decomposition of rank 7, 10, 16, and 32. In both cases (A and B), nearly all components are highly correlated with each other when the rank is 7 and 32. Ranks of 10 and 16 show plausible correlation values with non-correlated pairs of components.
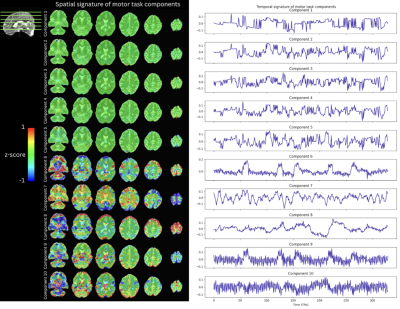
Spatial (z-scored) and temporal signatures of a rank 10 tensor decomposition of the motor task data.
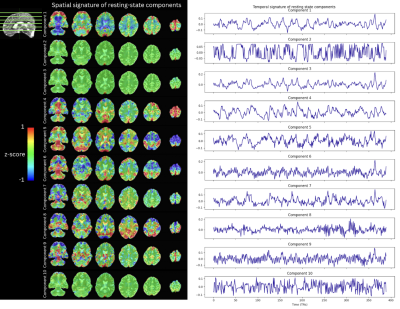
Spatial (z-scored) and temporal signatures of a rank 10 tensor decomposition of the resting-state data.
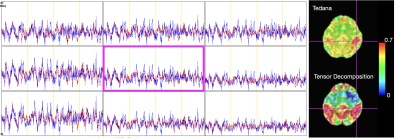
Timecourses of the optimally combined multi-echo resting-state data (black), tedana-denoised optimally combined data (blue), and optimally combined data denoised after tensor decomposition (blue) for the voxels pointed by the pink cross. The maps on the right show seed connectivity calculated on the data denoised with tedana and tensor decomposition. The seed is indicated by the pink cross.
DOI: https://doi.org/10.58530/2023/2668