2443

On Intra-Voxel Dephasing in Liver Diffusion-Weighted Imaging

Johannes Raspe¹, Sean McTavish¹, Kilian Weiss², Johannes M. Peeters³, Dimitrios C. Karampinos¹, and Anh T. Van¹
¹Department of Diagnostic and Interventional Radiology, School of Medicine, Klinikum rechts der Isar, Technical University of Munich, Munich, Germany, ²Philips GmbH Market DACH, Hamburg, Germany, ³Philips Healthcare, Eindhoven, Netherlands

Synopsis

Keywords: Liver, Diffusion/other diffusion imaging techniques

Motion is a major source of artifacts in liver diffusion-weighted (DW) imaging leading to severe signal loss. Physical information about motion is encoded in the phase of DW images based on a pulsed gradient spin-echo (PGSE) sequence. The present work proposes a methodology to estimate a phase-predicted attenuation (PPA) which correlates with the magnitude variation of DW images in motion-controlled phantom experiments and in vivo measurements. These phase-based predictions allow to isolate motion-related magnitude attenuation for further investigation of undesired signal loss effects and offer potential for refining algorithms to reduce magnitude loss in DW imaging of the liver.

Introduction

Diffusion-weighted (DW) imaging in the liver has a multitude of applications including clinical routine oncological imaging^1-4. Motion during pulsed gradient spin-echo (PGSE) based diffusion-encoding can cause signal loss^1,5,6. Due to moving anatomies like the heart and lungs in its vicinity, the liver is particularly affected^5,7. Even in respiratory-triggered acquisitions, severe signal loss can be observed in liver DW images, especially in the left lobe.^5,7,8. When the signal loss maps are known, adaptive repetition averaging algorithms can be employed to reduce signal loss in the averaged DW images^7,9-13. However, the estimation of the signal loss map is non-trivial due to the lack of reliable reference images. Since the motion is captured in the phase of the DW image, motion-induced signal loss can potentially be estimated from the phase without the need of a reference image. The present abstract studies the phase in PGSE sequence based DW single-shot echo-planar imaging (ssEPI) in the liver and proposes a methodology to estimate a phase-predicted attenuation (PPA) of the signal.

Methods

Intra-Voxel Dephasing
Motion during diffusion-encoding adds a phase $$$\varphi(\mathbf{r})$$$¹⁴ that is constant for translational¹⁵, linear for rotational¹⁶ and more complicated for other motion patterns. The signal loss inside an area $$$\mathcal{S}$$$ due to this phase is characterized by $$\mu(\mathcal{S})=\iint_{\mathcal{S}}{\mathrm{e}^{\mathrm{i}\varphi(\mathbf{r})}\,\mathrm{d}\mathbf{r}}.\;(1)$$ Assuming that motion is approximately rigid in a small enough region, the phase can be approximated to be linear inside this region: $$\varphi(\mathbf{r})=\varphi(x,\,y)=\alpha\,x+\beta\,y,\;(2)$$ with two linear coefficients $$$\alpha$$$ and $$$\beta$$$, neglecting the constant offset term, and $$$x$$$ and $$$y$$$ being the continuous in-plane coordinates. Using $$$\mathrm{Eq.}\,(2)$$$ in $$$\mathrm{Eq.}\,(1)$$$ yields the PPA approximation for a square region $$\mu=\int_{-\frac{\delta}{2}}^{\frac{\delta}{2}}{\int_{-\frac{\delta}{2}}^{\frac{\delta}{2}}{\mathrm{e}^{\mathrm{i}(\alpha\,x+\beta\,y)}\,\mathrm{d}x}\mathrm{d}y}=\delta^2\mathrm{sinc}\left(\frac{\delta \alpha}{2}\right)\mathrm{sinc}\left(\frac{\delta \beta}{2}\right).\;(3)$$

Linear Phase Approximation
The local slope of the phase of an image can be estimated by taking the difference between the phase of the image and its spatially shifted version. This cannot be achieved by a simple subtraction because of the wrapping nature of the phase but is instead done by taking the phase of the complex product $$I(\mathbf{r})I^*(\mathbf{r}')=|I(\mathbf{r})||I^*(\mathbf{r}')|\mathrm{e}^{\mathrm{i}(\varphi(\mathbf{r})-\varphi(\mathbf{r}'))},\;(4)$$ where $$$I$$$ represents the image. Using $$$\mathbf{r}=(i,j)$$$ and $$$\mathbf{r}'=(i+1,j)$$$ yields a map of $$$\alpha(i,j)$$$ for each discrete image location $$$(i,j)$$$ and using $$$\mathbf{r}'=(i,j+1)$$$ consequently gives $$$\beta(i,j)$$$. The PPA map is finally computed using $$$\mathrm{Eq.}\,(3)$$$ with $$$\delta = 1$$$ with subsequent smoothing.

Data Acquisition
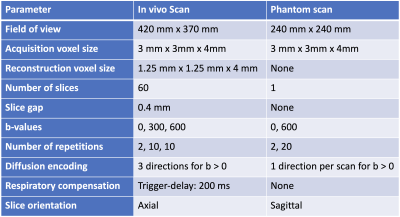
All scans were performed on a 3T whole-body scanner (Ingenia Elition X, Philips Healthcare, The Netherlands). A pineapple phantom was used and placed with its core perpendicular to the magnet bore inside a 16-channel head coil. A spin-echo DW sequence with a ssEPI readout was employed. Diffusion-encoding was only applied along one direction per scan. The pineapple was poked in the second half of each of the three scans to create rotational motion with the rotation vector roughly along the core of the pineapple. Additionally, a volunteer was scanned using a 16-channel torso coil and a 12-channel posterior coil - compare $$$\mathrm{Tab.}\,1$$$.

Results

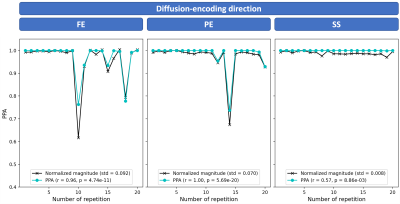
Phantom Data
Magnitude and phase images as well as PPA maps of the pineapple phantom can be seen in $$$\mathrm{Fig.}\,1$$$. There is no considerable phase accumulation observable in the stationary case shown in the first column of each diffusion-encoding direction. During motion, there is stronger phase accumulation in images with in-plane diffusion-encoding directions. The analysis in $$$\mathrm{Fig.}\,2$$$ shows a high correlation between magnitude variation and PPA in the frequency encode (FE)- and phase encode (PE)-directions where signal varies due to motion.
In Vivo Data
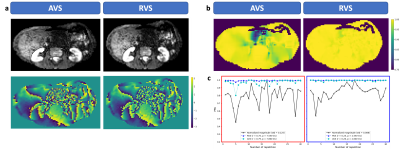
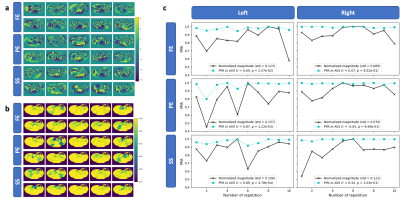
Examples of magnitude and phase DW images from a volunteer are displayed in $$$\mathrm{Fig.}\,3$$$(a) with acquisition voxel size (AVS) on the left and in-plane reconstruction voxel size (RVS) on the right. The PPA maps in $$$\mathrm{Fig.}\,3$$$(b) show that attenuation is estimated to be much smaller using the RVS. An analysis in two regions of interest (ROIs) in $$$\mathrm{Fig.}\,3$$$(c) shows a good correlation between PPA and magnitude variation but also a gap between the respective curves. Nevertheless, the AVS curve is closer in predicting the signal variation. The phase images of the representative images from the same slice as depicted in $$$\mathrm{Fig.}\,3$$$ are displayed in $$$\mathrm{Fig.}\,4$$$(a) together with the respective PPA maps in $$$\mathrm{Fig.}\,4$$$(b). Magnitude signal and PPA correlate well in the left liver lobe but not in the right liver lobe as shown in $$$\mathrm{Fig.}\,4$$$(c).

Discussion

A method to compute the signal attenuation encoded in the phase was introduced and compared to the magnitude signal variation. A good correlation between magnitude and PPA is observable in the phantom scans and in vivo. However, the correlation in vivo is weaker and not significant which may be due to other factors that are not accounted for as in the phantom experiment. Interpolation to RVS is obstructive for the computation since in the interpolation step, the relationship between neighboring pixels also gets interpolated and diminishes the actual phase slope. The good correlation between magnitude and PPA illustrates that information about motion is encoded in the phase which can potentially be used as a physically informed predictor for signal loss for example for robust weighted averaging^10,11,13,17 or as additional input to a neural network^10,12. Nonetheless, there is a discrepancy between the amount of magnitude variation and the PPA that may be explained by through-plane phase modulation or other factors and further investigations are warranted.

Acknowledgements

The present research was supported by Philips Healthcare and the German Research Foundation (project number 455422993/FOR5298-iMAGO-P1).

References

[1] Elizabeth M.~Charles-Edwards and Nandita M.~deSouza. Diffusion-weighted magnetic resonance imaging and its application to cancer. Cancer imaging 2006; 6(1):135-143

[2] Dow-Mu Koh and David J.~Collins. Diffusion-Weighted MRI in the Body: Applications and Challenges in Oncology. American Journal of Roentgenology 2007; 188(6):1622-1635

[3] Petra G.~Kele and Eric J.~van der Jagt. Diffusion weighted imaging in the liver. World journal of gastroenterology: WJG 2010; 16(13):1567-1576

[4] Camelo Messina et al. Diffusion-Weighted Imaging in Oncology: An Update. Cancers 2020; 12(6):1493

[5] Thomas C~Kwee et al. Influence of cardiac motion on diffusion-weighted magnetic resonance imaging of the liver. Magnetic Resonance Materials in Physics, Biology and Medicine 2009; 22:319-325

[6] Vinai M.~Pai et al. PCATMIP: Enhancing signal intensity in diffusion-weighted magnetic resonance imaging. Magnetic Resonance in Medicine 2011; 65(6):1611-1619

[7] Joy Liau et al. Cardiac motion in diffusion-weighted MRI of the liver: artifact and a method of correction. Journal of Magnetic Resonance Imaging 2012; 35(2):318-327

[8] Shinji Naganawa et al. Diffusion-weighted Imaging of the Liver: Technical Challenges and Prospects for the Future. Magnetic Resonance in Medical Sciences 2005; 4(4):175-186

[9] Shintaro Ishikawa et al. Improving the Quality of Diffusion-weighted Imaging of the Left Hepatic Lobe Using Weighted Averaging of Signals from Multiple Excitations. Magnetic Resonance in Medical Sciences 2019; 18(3):225-232

[10] Fasil Gadjimuradov et al. Deep Learning-based Adaptive Image Combination for Signal-Dropout Suppression in Liver DWI. In: Proceedings of the 29th Annual Meeting of the ISMRM, Virtual Conference 2021; 0534

[11] Tobit Führes et al. Postprocessing Reduces Pulsation Artifacts and Increases Visibility of Liver Lesions in Flow-compensated Diffusion-weighted Imaging. In: Proceedings of the 30th Annual Meeting of the ISMRM, London 2022; 1154

[12] Fasil Gudjamuradov et al. Deep Learning-Guided Weighted Averaging for Signal Dropout Compensation in DWI of the Liver. Magnetic Resonance in Medicine 2022; 88(6):2679-2693

[13] Johannes Raspe et al. Spatial Scaling of Respiratory-Triggered Liver Diffusion Weighted Imaging. In: Proceedings of the 30th Annual Meeting of the ISMRM, London 2022; 0032

[14] Jesper L.~R.~Andersson and Stefan Skare. Image distortion and its correction in diffusion MRI. Diffusion MRI: Theory, Methods, and Applications. Oxford University Press, Oxford 2010; 285-302

[15] Philippe C.~Douek et al. Myelin fiber orientation color mapping. In: 10th Annual Conference of the SMRM, San Francisco 1991

[16] Adam W.~Anderson and John C.~Gore. Analysis and correction of motion artifacts in diffusion weighted imaging. Magnetic Resonance in Medicine 1994; 32(3):379-387

[17] Anh T.~Van et al. SENSE-like reconstruction of multi-average body DWI to remove motion-induced signal loss: application in liver DWI. In: Proceedings of the 30th Annual Meeting of the ISMRM; 3283

Figures

Table 1. Scan parameters of the in vivo volunteer scan and the pineapple phantom scan.

Figure 1. The images in the rows are magnitude, phase and phase-predicted attenuation (PPA) maps of the pineapple phantom. Images in the first respective columns are not affected by motion and therefore no additional phase is accumulated. Images in the second columns are recorded during rotation and show signal loss, linear phase, and attenuation. Phase accumulation for diffusion-encoding along the frequency encode (FE) direction is observed along the phase-encode (PE) direction and vice versa. The effect in the slice selection (SS) direction is small with phase in both directions.

Figure 2. Analysis in a region of interest (ROI) placed in the center of the pineapple shows that there is no magnitude variation or PPA in the absence of motion in the first half of the scans while signal loss and phase accumulation can be observed for the FE and PE diffusion-encoding directions in the presence of motion. There is a high correlation between magnitude variation and PPA when the magnitude is varying ($$$r = 0.96$$$ for FE and $$$r = 1.00$$$ for PE). No considerable correlation is observable in the SS direction.

Figure 3(a). Magnitude and phase images of a representative slice of the volunteer scan in the top and bottom rows with acquisition voxel size (AVS) on the left and reconstruction voxel size (RVS) on the right. (b) The PPA map calculated from AVS on the left shows greater attenuation than the map calculated from RVS on the right. (c) The normalized magnitude of two ROIs indicated by the same colored squares in (a) varies more in the left compared to the right lobe. PPA correlates with magnitude and is closer for the AVS but the correlation is not significant.

Figure 4(a). Phase images of the volunteer with diffusion-encoding along FE-, PE-, and SS-directions. (b) PPA maps for the same images give a visual correlation between areas of high attenuation and high spatial phase variation. (c) The analysis in the same ROIs as before shows higher magnitude variation in the left liver lobe and a good correlation with the PPA ($$$r = 0.69$$$ for FE, $$$r = 0.87$$$ for PE and $$$r = 0.89$$$ for SS in the left liver lobe). The correlation in the right lobe ROI is much smaller in the absence of big phase variations due to a smaller effect of motion.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

2443

DOI: https://doi.org/10.58530/2023/2443