2435
Differentiating Benign from Malignant Liver Lesions Using Non-Gaussian Models of Diffusion Weighted MRI1Sun Yat-Sen Memorial Hospital, Guangzhou, China, 2Sun Yat-Sen University, Guangzhou, China, 3MR Scientific Marketing, Siemens Healthineers Ltd, Guangzhou, China
Synopsis
Keywords: Liver, Diffusion/other diffusion imaging techniques
This study aimed to evaluate the feasibility of various diffusion metrics obtained from stretched exponential model (SEM), diffusion kurtosis (DK) and fractional-order calculus (FROC) models -based diffusion-weighted imaging (DWI) in differentiating benign from malignant liver lesions. The results demonstrated that, as non-Gaussian DWI models, the combination of SEM and FROC models showed good discriminative ability, which was able to differentiate benign and malignant liver lesions.Introduction
Liver nodules are commonly encountered on clinical practice with extensive differential diagnosis, and the incidence of liver lesions detection has increased in the recent decades [1]. Accurate preoperative diagnosis and identification of liver lesions are essential in determining the optimal treatment strategies. Diffusion-weighted imaging (DWI) is a widely used magnetic resonance imaging (MRI) sequence that facilitates the detection and preoperative characterization of liver lesions [2, 3]. Recognizing that information on tissue microstructures or heterogeneity is not directly reflected by the prevailing mono-exponential models, many studies have proposed more sophisticated non-Gaussian diffusion models in an attempt to extract additional tissue structural information [4]. The stretched-exponential model (SEM) proposed by Bennett et al. [5] can be used to evaluate distributed diffusion and intravoxel heterogeneity. The diffusion kurtosis model has been used to reflect the complexity of tissue microstructure and provide a more comprehensive characterization of water diffusion [6]. Furthermore, the fractional order calculus (FROC) model features a new set of parameters to describe the anomalous diffusion process in complex biologic tissues [7]. These non-Gaussian diffusion models are free from the assumption of Gaussian diffusion and they can provide additional imaging metrics reflecting microstructure. Prior researches have explored the SEM [8] or DKI [9] model in the assessment of liver lesions, however for the FROC model, to the best of our knowledge, it has not been applied in characterizing liver lesions. Thus, the aim of this study was to explore the feasibility of three non-Gaussian diffusion models including SEM, DKI and FROC model in differentiating between benign and malignant lesions.Methods
A total of 30 patients with liver tumors diagnosed via histopathology were prospectively included, including 18 malignant tumors and 12 benign nodules. All patients underwent liver MRI on a 3T MR scanner (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) with a phased array body coil. MR examinations, including conventional T1-, T2-weighted imaging, dynamic contrast-enhanced (DCE)-MRI and DWI, were performed. The DWI data was acquired by using a single-shot echo planar imaging (EPI) sequence with 15 b values of 0, 10, 20, 30, 50, 70, 100, 200, 400, 600, 800, 1000, 1500, 2000, 2500, 3000 s/mm2. The imaging parameters were as follows: TE=101 ms, TR=2000 ms, field of view = 350 × 350 mm2, acquisition matrix = 174 × 174, slice thickness = 5.2 mm. DWI-derived parameters, including distributed diffusion coefficient (DDC) and the heterogeneity index (α) derived from SEM, the diffusivity (DK) and mean kurtosis (K) from DKI, as well as diffusion coefficient (D), fractional order derivative in space (β) and spatial metric (μ) sourced from FROC, were calculated using a unified in-house developed software called BoDiLab, which is based on Python 3.7. The average of all diffusion parameters of each patient's liver lesion were recorded for statistical analysis. Differences in DDC, α, DK, K, D, β and μ values between benign and malignant liver lesions were evaluated by using the Mann–Whitney U-test. Multivariate logistic regression was used to combine diffusion parameters for differentiating benign and malignant liver tumors. Receiver operating characteristic (ROC) analysis was performed to determine the performance of each individual parameter as well as the combination of selected parameters for tumor differentiation. All statistical analyses were performed using SPSS with a statistical significance set at P < 0.05.Results
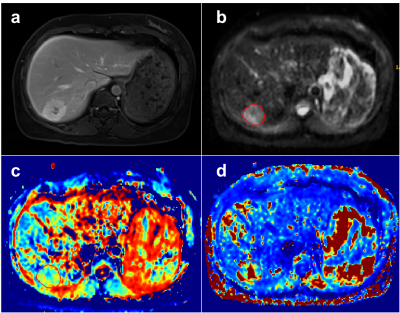
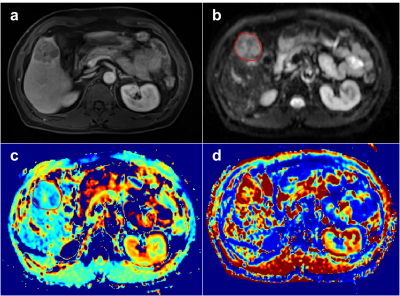
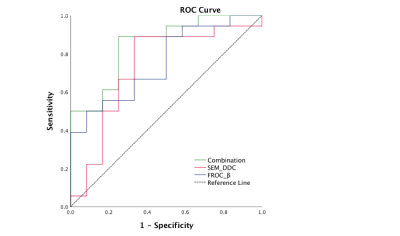
Representative figures of benign and malignant liver tumors are shown in Figures. 1 and 2. The mean values of DDC, D and β of liver benign lesions were significantly increased compared with that of malignant liver tumors (P=0.039, 0.039, 0.019). However, α, DK, K and μ showed no differences between benign and malignant liver tumors. Multivariate logistic regression analysis based on the combination of DDC and β produced the higher AUCs (0.847) than the individual AUCs of DDC (0.727) and β (0.755) (Figure 3).Discussion & Conclusion
In our study, DDC derived from SEM and β derived from FROC model can be used in the differentiation of benign and malignant liver tumors, and the combination of them showed better diagnostic performance compared with individual parameters. Consistent with previous research [8], our study also found that DDC was able to distinguish malignant liver tumors from benign lesions, which may be associated to the higher density of cells and stroma of malignant lesions that restricts the movement of water in tissue with respect to benign lesions. β derived from FROC model, as a novel indicator describing the fractional-order dynamics in space, is inversely related to the degree of heterogeneity and complexity of tumor microstructure [10, 11]. Our study demonstrated that liver malignant tumors showed significantly lower β values compared with benign nodules, indicating a higher degree of tissue heterogeneity within malignant tumors. More importantly, our study revealed that the combination of DDC and β further improved the performance for tumor differentiation. Therefore, non-Gaussian diffusion model is valuable for characterizing liver lesions, and may contribute to better understanding of pathophysiology of liver tumors.Acknowledgements
NoReferences
1. Lee, J.M., et al., Recent Advances in CT and MR Imaging for Evaluation of Hepatocellular Carcinoma. Liver Cancer, 2012. 1(1): p. 22-40.
2. Parikh, T., et al., Focal liver lesion detection and characterization with diffusion-weighted MR imaging: comparison with standard breath-hold T2-weighted imaging. Radiology, 2008. 246(3): p. 812-22.
3. Taouli, B. and D.M. Koh, Diffusion-weighted MR imaging of the liver. Radiology, 2010. 254(1): p. 47-66.
4. Tramontano, L., et al., The Role of Non-Gaussian Models of Diffusion Weighted MRI in Hepatocellular Carcinoma: A Systematic Review. J Clin Med, 2021. 10(12).
5. Bennett, K.M., et al., Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn Reson Med, 2003. 50(4): p. 727-34.
6. Jensen, J.H. and J.A. Helpern, MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed, 2010. 23(7): p. 698-710.
7. Magin, R.L., et al., Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson, 2008. 190(2): p. 255-70.
8. Kim, H.C., et al., Characterization of focal liver lesions using the stretched exponential model: comparison with monoexponential and biexponential diffusion-weighted magnetic resonance imaging. Eur Radiol, 2019. 29(9): p. 5111-5120.
9. Jia, Y., et al., Diffusion Kurtosis MR Imaging versus Conventional Diffusion-Weighted Imaging for Distinguishing Hepatocellular Carcinoma from Benign Hepatic Nodules. Contrast Media Mol Imaging, 2019. 2019: p. 2030147.
10. Tang, L., et al., Non-Gaussian diffusion imaging with a fractional order calculus model to predict response of gastrointestinal stromal tumor to second-line sunitinib therapy. Magn Reson Med, 2018. 79(3): p. 1399-1406.
11. Liu, G., et al., Comparison of mono-exponential, bi-exponential, kurtosis, and fractional-order calculus models of diffusion-weighted imaging in characterizing prostate lesions in transition zone. Abdom Radiol (NY), 2021. 46(6): p. 2740-2750.
Figures