2407
Simulation tool for non-Fourier MRSI reconstruction1Wolfson Brain Imaging Centre, Department of Clinical Neuroscience, University of Cambridge, Cambridge, United Kingdom, 2University of Cambridge, Cambridge, United Kingdom
Synopsis
Keywords: Software Tools, Spectroscopy, non-cartesian MRSI
With the wider availability of ultra-high field MR systems, metabolic imaging using MRSI is a fast-developing area of research. Frequently used sequences use non-uniformly sampled trajectories to achieve high-acceleration factors e.g. concentric-ring trajectories (CRT). In this work, we demonstrate the from-scratch implementation of a simulation and reconstruction tool for CRT-MRSI using (1) a regridding, (2) an iterative L2 linear solver as well as (3) applying the non-uniform FFT implementation from the BART-toolbox to simulated non-cartesian MRSI data with a known Fourier-transform pair. The exact sampled data permits the evaluation of the impact of different reconstruction implementations.Introduction
Fast MRSI methods require high acceleration factors, in comparison to traditional phase-encoded CSI. A common approach for high-resolution MRSI is spatial-spectral sampling using non-cartesian trajectories1. These are advantageous over cartesian trajectories due to the flexibility in balancing optimised sampling pattern design with hardware constraints. A down-side of using non-uniform sampling, however, is that the standard 2D Fast-Fourier Transform (FFT) algorithm cannot be used for the solution of the inverse problem. Thus, alternative reconstruction methods need to be applied to the sampled data. There are generally two approaches for MRSI. (A) Gridding onto a cartesian grid before performing the spatial 2D-FFT, followed by spectral processing and (B) iterative optimisation of the inverse problem. In this work, we implement a simple, from-scratch simulation and reconstruction method which can be used for non-uniformly sampled k-space trajectories. We demonstrate the usage on a set of concentric-ring trajectories (CRT) for a geometric spectroscopic phantom.Methods
k-space trajectories and definitions of an ellipsoid test object were used to determine the non-uniformly sampled k-space samples. Since the analytical Fourier of an ellipsoid is given by the Bessel functions of the first kind J1, exact k-space samples were determined for the given test object. Spectral simulations included frequency modulation, magnitude scaling and exponential T2 decays. Three approaches for the reconstruction of the non-uniformly sampled data were implemented.- Spatial gridding with linear interpolation (“griddata”)
- Iterative reconstruction using a L2 linear solver (“minres”)
- Iterative reconstruction using the inverse nufft algorithm from the Berkeley Advanced Reconstruction Toolbox (BART)2.
All signal simulations and reconstructions were implemented in MATLAB (R2021b, Mathworks).
Results
Figure 1 shows the workflow of the simulation tool for the generation of exact non-cartesian sample data. This can be used on any arbitrary k-trajectory, when a test object with an analytical Fourier transform is equally sampled in the temporal domain.The reconstruction implementation was demonstrated on five distinct concentric-ring trajectories (Figure 2) highlighting different aspects of CRT variations i.e. equidistant or density-weighted trajectories, as well as the impact of sampling sparsity.
Reconstruction results for the three different methods are shown in Figure 3. Note the distinct differences in scaling, and the impact of sparse sampling on the image reconstruction.
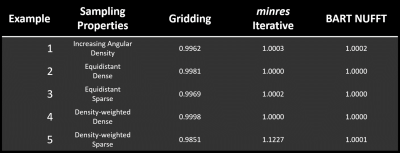
The NRMSE for each reconstruction approach is given in Table 1.
Discussion & Conlcusion
We demonstrated a simulation and reconstruction tool for non-cartesian MRSI which can be used on arbitrary sampling trajectories. Future work may include simulation of imperfections including off-resonance effects and gradient imperfections. The use of test objects which have an analytical Fourier transform allows measuring the impact that different reconstruction pipelines for non-cartesian data have as shown by comparing the three reconstruction methods.The simulation and reconstruction source code will be made available on GitHub3.
Acknowledgements
The Wolfson Brain Imaging Centre is supported by the NIHR Cambridge Biomedical Research Centre and an MRC Clinical Research Infrastructure Award for 7T research. CG is supported by a Cambridge European Scholarship awarded by the Cambridge Trust and the W.D. Armstrong Studentship in Engineering and Medicine. CTR is funded by the Wellcome Trust and the Royal Society [098436/Z/12/B]. This work was supported by Innovate UK [10032205] under the Guarantee Scheme relating to the EU Horizon Europe project MITI [101058229] and European Union’s H2020 research and innovation program under grant agreement [801075].References
1. Bogner W, Otazo R, Henning A. Accelerated MR spectroscopic imaging-a review of current and emerging techniques. NMR Biomed. John Wiley and Sons Ltd; 2020;2020/05/14:e4314.
2. Martin Uecker, Frank Ong, Jonathan I Tamir, Dara Bahri, Patrick Virtue, Joseph Y Cheng, Tao Zhang, and Michael Lustig. Berkeley Advanced Reconstruction Toolbox. Annual Meeting ISMRM, Toronto 2015, In Proc. Intl. Soc. Mag. Reson. Med. 23:2486
3. https://github.com/brainchemie/non-uniform_MRSI_Reconstruction.git
Figures
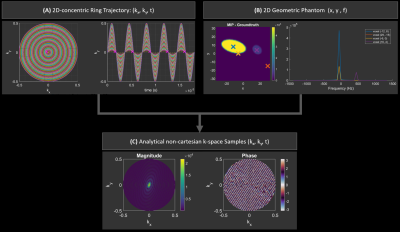
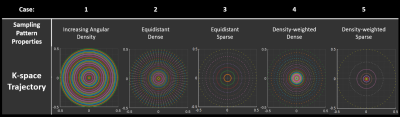
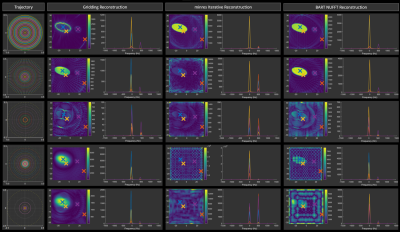
Figure 3: Reconstruction results showing maximum intensity projections along the spectral domain of the absolute spectrum for all five trajectories. The absolute spectra at four sample points are also shown. Note that the gridding reconstruction performs well in all cases but Case 3, highlighting the importance of a highly sampled k-space centre.