Synopsis

Keywords: Machine Learning/Artificial Intelligence, Diffusion/other diffusion imaging techniques, NODDI

Deep learning has a great potential for estimating brain tissue micro-structure from diffusion MRI measurements. However, it is hard to understand and interpret how these models work. Therefore, until now these deep learning models have been designed using ad-hoc approaches. In this work, we propose a method for determining the contribution of different measurements to the prediction produced by these deep learning models. We apply this method for estimating the parameters of the NODDI model for the neonatal brain. Results show that this method is highly effective in determining the subsets of the measurements that result in lower estimation error.

Introduction

Deep learning (DL) models have shown great promise in estimating brain tissue micro-structure from under-sampled diffusion MRI (dMRI) measurements. However, given the black-box nature of these models and the complexity of the relation between tissue micro-structure and the dMRI signal, understanding the inner workings of these models is a challenging task that has not been attempted before. No prior work has analyzed the dependence of these models on the dMRI measurements in a systematic way. As a result, these DL models have been designed using ad-hoc approaches that may result in highly sub-optimal models. A technique that can determine the contribution of different measurements to the prediction would be of high practical value. Such a technique can identify the measurements that are most critical for the prediction task and those that have insignificant contribution, thereby informing us in designing more accurate models as well as in acquiring the most useful measurements in the limited scan time.

Methods

Model
In this work, we focus on two brain micro-structure parameters from the NODDI model¹: Orientation Dispersion Index (ODI) and Neurite Density Index (NDI). These are powerful biomarkers of brain development and degeneration. Figure 1 describes the DL model that we use to estimate these parameters from multi-shell dMRI data.

Methods
Consider a function $$$y= f(X)$$$ that estimates $$$y$$$ from measurements $$$X \in \mathbb{R}^m$$$. It is often highly desirable to know the contribution of each measurement, or subset of measurements, to the estimation of $$$y$$$. The brute-force approach is to examine all possible measurement combinations, but even when m=30 there will be more than a billion combinations.
We propose a method based on Quantitative Input Influence (QII) measures². Using QII, the marginal contribution of measurement $$$i$$$ over a given measurement set $$$S$$$ can be estimated as²:
$$\text{QII}(i, S)= \mathop{\mathbb{E}} ( f(X_{-S} U_S) - f(X_{-S \cup i} U_{S \cup i}) )$$
where $$$-S$$$ denotes inputs that are not in $$$S$$$ and $$$U$$$ is an intervention distribution. In this work, we choose $$$U$$$ to be the distribution of the mean of the measurement that is to be intervened (i.e., shell and gradient direction) computed over the training data. Based on QII, we propose a new measure for quantifying the power of a subset of the measurements for computing the parameter of interest. We call this new measure the Measurement Subset Prediction Power (MSPP), and define it as follows:
$$\text{MSPP}(S)= \mathop{{}\mathbb{E}}_{S^* \subseteq S} ( \text{QII}(S^*, S \setminus S^*) - \mathop{{}\mathbb{E}}_{S^* \subseteq \{1, ..., m \} \setminus S } ( \text{QII}(S^*, S) ) )$$
Highly accurate approximations of QII and MSPP can be efficiently computed using Monte-Carlo sampling methods. MSPP allows us to compare the prediction power of different measurement subsets for estimating the parameters of interest.

Data and experiments
We use dMRI scans of 90 subjects from the dHCP dataset³; 60 subjects are used for training and 30 subjects for test. Each dMRI scan has 300 measurements in three shells: b=0 (n=20), b=400 (n=64), b=1000 (n=88), b=2600 (n=128). In order to compute the reference ground-truth ODI and NDI images for training and evaluation, we apply an optimization-based method implemented in Dmipy⁴ on all 300 measurements. Highly under-sampled subsets of the measurements are used with the proposed deep learning method and Dmipy to reconstruct ODI and NDI images, which are compared with the ground truth to compute the error.

Results

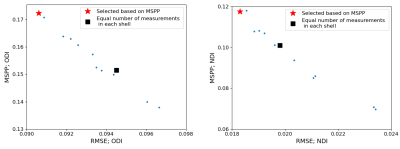
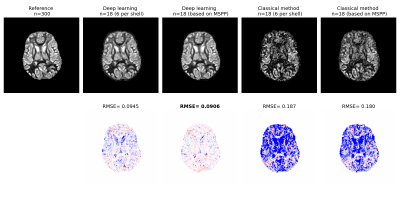
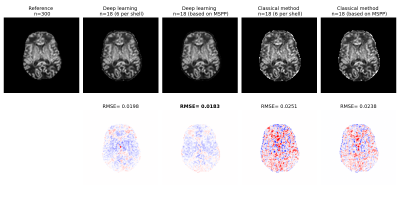
Figure 2 shows plots of MSPP versus the root mean square of estimation error (RMSE) for ODI and NDI. To compute the RMSE we trained a new deep learning model with the selected measurement subset from scratch, whereas MSPP values were computed using a single model trained with all measurements using Equation 2. The proposed MSPP has a mostly monotonic relation with estimation error. This suggests that MSPP can be used as a reliable surrogate for RMSE in choosing the measurements that result in lower estimation error, thereby removing the need to train a new model for every subset of measurements.
Figures 3 and 4 show example ODI and NDI images reconstructed from 18 measurements with the proposed deep learning method and a classical optimization-based method implemented in Dmipy. Dmipy was also used to compute the reference ground truth using 300 measurements. These figures show the results with two different subsets of 18 measurements: (i) Equal number of six measurements from each shell, and (ii) Measurements in each shell selected based on MSPP. The results show lower RMSE for the deep learning method than for Dmipy. They also show lower RMSE with the measurements selected based on MSPP. For both ODI and NDI, statistical analysis on test subjects showed that the RMSE for the deep learning method was significantly ($$$p<0.001$$$) lower than for Dmipy, and that the RMSE achieved with the measurements selected based on MSPP was significantly ($$$p<0.001$$$) lower than when equal number of measurements in each shell were selected.

Conclusion

Model explainability techniques based on QII can be used to determine the most informative diffusion MRI measurements for estimating brain microstructure. Such techniques can be of high practical value as they can 1) help us design more accurate models, and 2) determine the measurements that should be acquired to achieve lower estimation error.

Acknowledgements

This research was partly supported by the US National Institutes of Health (NIH) under awards R01NS106030 and R01EB032366; by the Office of the Director of the NIH under award S10OD0250111; and by NVIDIA Corporation; and utilized an NVIDIA RTX A6000 GPU and RTX A5000 GPUs.. This work was partly supported by a Mobility grant from the Swiss National Science Foundation (project 205321-182602). We acknowledge the CIBM Center for Biomedical Imaging, a Swiss research center of excellence founded and supported by CHUV, UNIL, EPFL, UNIGE, HUG and the Leenaards and Jeantet Foundations. Newborn data were provided by the developing Human Connectome Project, KCL-Imperial-Oxford Consortium funded by the European Research Council under the European Union Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement no. [319456]. We are grateful to the families who generously supported this trial.