Synopsis

Keywords: Pulse Sequence Design, Brain

Half-Fourier acquisition single-shot turbo spin-echo diffusion-weighted is a clinically established magnetic resonance imaging tool for the detection of small lesions, particularly cholesteatoma. However, in the standard approach, half of the available signal is sacrificed through displacing one echo parity out of the acquisition window to fulfill the Carr-Purcell-Meiboom-Gill condition. We present a selective parity approach to tackle this problem. The proposed method features a near full sensitivity, a low specific absorption rate for long echo trains, and more than two-fold increase in signal-to-noise ratio, compared to the manufacturer's method under the same conditions.

Introduction

Fast spin echo sequence (FSE) is a popular sequence in clinical imaging because of its high sensitivity and high immunity against B₀ inhomogeneity artifacts. However, a prerequisite for its successful application in DWI is the fulfillment of the Carr-Purcell-Meiboom-Gill (CPMG) condition, which is often violated due to the bulk motion. Existing solutions to this problem typically sacrifice half the signal intensity by eliminating interference between anti-CPMG components. Diffusion-weighted half-Fourier acquisition single-shot turbo spin-echo (DW-HASTE) is a variant of the FSE method, which has found widespread applications in detecting small lesions.

In this work, we present our recent developments in DW-HASTE with the selective parity approach, initially introduced in [1] and further developed in [2-3], and optimize the sequence for 3T in the context of multiple receive coil reception and parallel imaging.

Theory

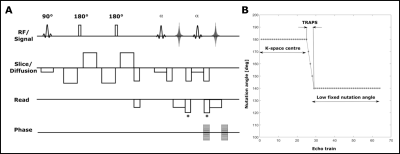
Acquisition: To avoid image artifacts caused by anti-CPMG components, the oldest and most commonly used approach is to acquire only one of the echo parities, while the other one is displaced out of the acquisition window, halving the sensitivity to the signal [4-6]. To address this problem, displacing gradients were implemented to preserve the full sensitivity of the method through benefiting from the contribution of both echo parities in the signal, by displacing the signal parity with the lowest contribution at each echo (figure 1A).

Shinnar Le-Roux (SLR) refocusing pulses were employed for their better slice profiles resulting in smooth echo amplitude decay over early echoes. This makes the use of dummy cycles for the echo amplitude stabilization unnecessary, and ultimately offers a shorter echo time compared to the manufacturer’s method.

Smooth transition between pseudo steady states (TRAPS [7-8]) was employed to decrease the SAR contribution from the SLR pulses (figure 1B).

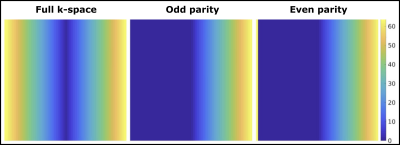
A modified center-out phase encoding scheme (figure 2) was employed to sample the k-space in the order of 0 ^O,1 ^E,1 ^O,2 ^E,2 ^O,3 ^E,3 ^O,4 ^E, … where number represents the k-space coordinate and superscript is the echo parity (odd or even). This scheme is advantageous to account for the effects of any potential rotational movements during the strong diffusion encoding gradients, which can potentially displace the k-space origin in opposite directions for echo parities.

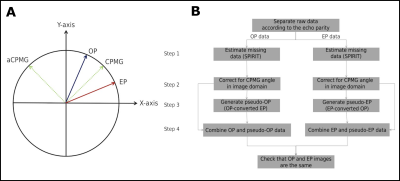
Reconstruction: Bulk motion during the strong diffusion encoding gradients causes both phase shifts and phase gradients in the image domain [9]. In SP-DW-HASTE data, odd and even echo parities experience those effects of the same magnitude, but opposite polarity. In addition, there is an arbitrary angle between the receiver and transmit phases for multi-channel receive arrays.

A novel reconstruction algorithm has been developed to deal with the above mentioned challenges (figure 3). Briefly, the acquired DW-SP-HASTE data were separated into OP and EP k-spaces (figure 2). An initial estimate of the missing data was generated with POCS-SPIRIT (step 1), and the orientation of the CPMG vector for each image voxel was fixed from a separate DW-SP-HASTE acquisition (b0). OP and EP data are the complex conjugates of each other in the frame of reference defined by the CPMG angle. Hence, by rotating both parity data by a negative CPMG angle (step 2), OP and EP data become the complex conjugates of each other around the X-axis with a simple interconversion (step 3). For instance, pseudo-OP and pseudo-EP data can be generated from EP and OP data, respectively, by applying the complex conjugate operation in the frequency domain. Finally, the full coverage k-space can be generated by combining either parity data and its pseudo-equivalent in the frequency domain.

Methods

MRI scans were performed on a whole body 3T Siemens Prisma scanner (80 mT/m strength and 200 mT/m/ms slew rate) with a 32-channel receive-only head coil in a healthy male volunteer. Data were collected with the manufacturer’s DW-HASTE and SP-DW-HASTE methods for b = 0 and 1000 s/mm². The common parameters were as follows: TR = 2000 ms, FOV = 210x153 mm², matrix size of 96x70, receiver bandwidth of 572 Hz/Px, 2.2 mm isotropic in-plane resolution, 3 mm slice thickness, and GRAPPA 3. The echo time and echo spacing were 61/6.93 ms for the SP-DW-HASTE, and 85/6.16 ms for the DW-HASTE. A whole brain dataset composed of 44 axial slices was acquired with a total scan time of 88s. Diffusion was encoded separately along read (r), phase (p) and slice (s) directions. Standard fat saturation was used for all acquisitions.

Results

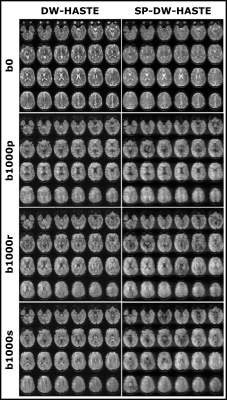
Example T₂-weighted (b0) and DW (b1000) images obtained with the SP-DW-HASTE and DW-HASTE methods are presented in figure 4. SNR analysis in a region-of-interest on the white matter region close to the ventricles on a sample slice revealed an SNR gain factor of 3.1 for b0, 2.9 for b1000p, 3 for b1000r, and 3.6 for b1000s from SP-DW-HASTE compared to the corresponding DW-HASTE data.

Discussion

Available methods for non-CPMG FSE imaging suffer mainly from low SNR and high SAR values, and their application is commonly limited to 1.5T. The presented approach addresses these problems through using both echo parities in the image formation, its shorter echo time, better slice profiles offered by the implemented SLR refocusing pulses, and applying variable flip angle refocusing pulses.