Synopsis

Keywords: Pulse Sequence Design, New Trajectories & Spatial Encoding Methods

Single-shot cross-term SPatiotemporal ENcoding (xSPEN) is a single-shot approach to MRI with exceptional resilience to field inhomogeneities. xSPEN’s non-Fourier nature and sinc-like point-spread function demands SNR/resolution compromises which, so far, no post-processing has managed to solve. This study shows that introducing a quadratic phase modulation in conjunction with the hyperbolic phase modulation demanded by xSPEN can solve this, enabling the use of deconvolution principles providing resolution enhancement. The principles and examples of the ensuing quadratic xSPEN (QxSPEN) experiment, are presented on synthetic, phantom and human brain single-shot data.

Introduction

Spatiotemporal encoding (SPEN)^1,2 and cross-term SPEN (xSPEN)^3,4 are single-shot 2D MRI protocols designed to alleviate EPI’s complications along the phase encoding dimension. xSPEN in particular has exceptional resilience to field inhomogeneities, enabling for instance single-shot acquisitions in clinical scanners in the presence of metallic implants.3 Like SPEN, xSPEN is a non-Fourier approach imaging the object directly in a spatial (y) domain; unlike SPEN, however, we have not found a way to “super-resolve” xSPEN data^5,6 –thereby paying a full $$$\sqrt {{\text{FOVy/}}\Delta {\text{y}}} $$$ penalty in its image’s SNR. This reflects xSPEN’s $$${e^{iC}}^{(y - yo)z}$$$ modulation, which when unraveled by a k_z wavenumber leads to a sinc-like imaging point spread function (PSF). Sincs have sharp low-passing effects stopping all high-frequency information which could enhance a voxel resolution, meaning the only way to enhance xSPEN’s resolution is by narrowing its $$$\Delta y$$$ –further decreasing sensitivity, while enhancing SAR. This work introduces a way of bypassing these limitations without giving up on xSPEN’s unique robustness, involving the application of a quadratic phase-modulation $$${e^i}^{C(y - yo)2}$$$ on top of xSPEN’s modulation. Breaking the $$$sinc$$$ PSF enables high-frequency components to come in, opening a route to a super-resolution deconvolution reconstruction where improved xSPEN SNR arises without losing resolution. Ways to implement these new QxSPEN experiments and to process their data are presented.

Methods

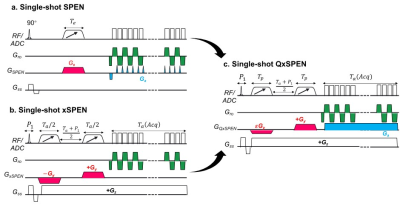
Figures 1a and 1b illustrate the SPEN and xSPEN single-shot imaging sequences. It follows from the modulations associated with these sequences that their respective signals will be
$${S_{SPEN}}\left( {{k_y}} \right) = \int {\rho \left( y \right){e^{i2\pi \left( { - C{{\left( {y - {y_o}} \right)}^2} + {k_y}y} \right)}}dy} \;\; \to \;\rho \left( y \right)\; \otimes \;{e^{i\beta {y^2}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)$$$${S_{xSPEN}}\left( {{k_z}} \right) = \int {\int {\rho \left( y \right){e^{i2\pi \left( { - {C^\prime }\left( {y - {y_o}} \right)z + {k_z}z} \right)}}dzdy} } \;\; \to \;\rho \left( y \right)\; \otimes \;sinc\left( {\alpha y} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2)$$where $$$\beta $$$ is related to C and k_y, $$$\alpha $$$ to $$$C'$$$ and k_z, and $$$ \otimes $$$ represents a convolution. In general, xSPEN’s resolution/sensitivity will depend on the $$$sinc$$$’s $$$\alpha $$$, and there is no way to improve one without degrading the other. As the $$${e^{i\beta {y^2}}}$$$ does not have the low-pass characteristics of $$$sinc\left( {\alpha y} \right)$$$, we alleviate this by introducing the quadratic + hyperbolic phase modulation shown in Fig. 1c. This QxSPEN variant combines xSPEN’s G_z readout defining the convolving kernel’s amplitude, with SPEN’s readout affecting the phase of this convolution. QxSPEN’s signal can be summarized as:$${S_{QxSPEN}}\left( {{k_y},{k_z}} \right) = \;\int {\int {{e^{i2\pi \left[ {\left( { - {C^\prime }\left( {y - {y_o}} \right) + {k_z}} \right)z} \right]}}dz} \;\rho \left( y \right)\;{e^{i2\pi \left[ { - C{{\left( {y - {y_o}} \right)}^2} + {k_y}y} \right]}}} dy \to \;\rho \left( y \right)\; \otimes \;[\;sinc\left( {\alpha y} \right) \cdot {e^{i\beta {y^2}}}\;](3)$$
It follows that a deconvolved (i.e., super-resolved) image $$$\rho (y)$$$ can be obtained from the acquired signal by dividing $$${\mathscr F}\left\{ {{S_{QxSPEN}}} \right\}$$$ by $$${\mathscr F}\left\{ {sinc\left( {\alpha y} \right) \cdot {e^{i\beta {y^2}}}} \right\}$$$ –accompanied if needed by a regularization– followed by an inverse FT.

To demonstrate this concept, simulations as well as phantom and in vivo experiments were executed with different convolution kernels, and processed accordingly. In vivo data were acquired following ethical approval and consent on human brains at 3T on a Siemens Prisma scanner using a 32-channel head coil. Acquisitions included single-shot EPI, xSPEN and QxSPEN with TR=2s, 230x230 mm² FOV, 4mm slice thickness, 64x64 image matrix size. Additional QxSPEN parameters included $$$\alpha = 0.22,\;0.15,\;0.17,\;0.12$$$ and $$$\beta = - 0.02,\; - 0.02,\; - 0.02,\; - 0.01$$$ .

Results and Discussion

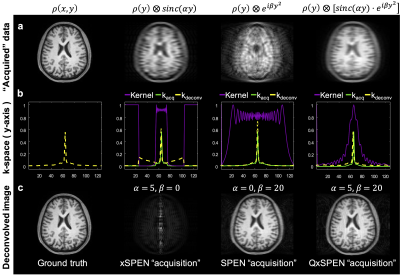
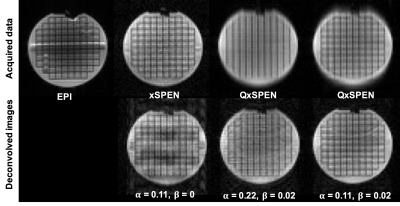
Figure 2 shows simulated SPEN, xSPEN and QxSPEN results for their different convolution kernels, together with their deconvolutions and with the “ground truth”. SPEN’s kernel is clearly amenable to deconvolution, whereas xSPEN’s $$$sinc$$$ kernel results in a narrowband rectangle-like low-pass k-space filter. Dividing by it amplifies high-frequency components by ≈0 denominators, ruining the deconvolution. Adding QxSPEN’s quadratic phase kernel solves this problem, leading to a good recovered image.

Figure 3 compares EPI, SPEN and QxSPEN images of a reticular phantom –the latter two collected with different $$$\alpha $$$ and $$$\beta $$$ parameters. Shown underneath the xSPEN and QxSPEN data are the expected deconvolutions. Once again, the improvement in resolution for QxSPEN is evident.

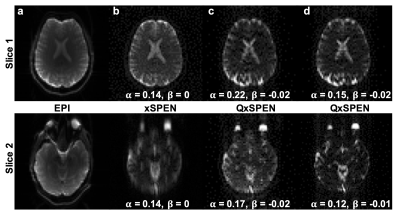
Figure 4 shows a similar set of comparisons, but for two in vivo brain slices (only deconvolved QxSPEN data now shown). Notice xSPEN’s avoidance of the distortions affecting EPI’s frontal region, which is well preserved by QxSPEN, as well as the resolution improvement brought by the latter’s deconvolution.

Conclusions

A new sequence enabling the deconvolution of xSPEN single shot images by the addition of a quadratic phase, was introduced and demonstrated. The ensuing QxSPEN is capable of improving in-plane resolution without degrading the SNR; additional features are under investigation.

Acknowledgements

We are grateful to Drs. Sagit Shushan, Amir Seginer and Edna Furman-Haran for assistance with the human experiments. This work was supported by the Minerva, Israel Science Foundations and National Natural Science Foundation of China (No. 62001290). KD acknowledges fellowships from Israel’s Planning and Budget Committee. LF heads the Clore Institute for High-Field Magnetic Resonance Imaging and Spectroscopy, whose support is also acknowledged.