2382
Optimized Phase Cycling for Coherence Pathway Selection in Pi Echo Planar Imaging
Mark Armstrong1 and Dan Xiao1
1University of Windsor, Windsor, ON, Canada
1University of Windsor, Windsor, ON, Canada
Synopsis
Keywords: Pulse Sequence Design, New Trajectories & Spatial Encoding Methods
Pi Echo Planar Imaging (PEPI) has a significantly reduced gradient duty cycle compared to FSE. It has a great potential for low field MRI where concomitant fields are significant. However, its application is limited due to the requirement of a near perfect refocusing pulse to avoid coherence pathway artifacts. In this work an optimized phase cycling scheme is proposed which minimizes coherence pathway contributions to the signal. This method has been validated in simulations and experiments showing a reduced sensitivity to flip angle compared to the conventional XY-16 method. Artifact-free 2D PEPI was achieved.Introduction
Fast Spin Echo (FSE) experiments provide good quality images in a rapid acquisition. For high resolution imaging, high gradient duty cycle is required in FSE, which may lead to significant concomitant field effects in low field imaging. The Pi Echo Planar Imaging (PEPI)1 sequence employs unbalanced gradients, allowing phase accumulation over the entire echo train, so that the gradient duty cycle can be drastically reduced. A shorter echo spacing may also be achieved. PEPI requires near ideal 180° refocusing pulses to eliminate the coherence pathway artifacts, which has limited its application to 3D imaging of small subjects confined to the homogeneous region of the RF coil. Sufficient quality 2D PEPI could not be obtained due to the imperfect slice profile. In this work, an optimized phase cycling scheme is proposed to minimize coherence pathway artifacts in the PEPI experiments with non-ideal refocusing RF pulses and to enable 2D PEPI imaging.Methods
The phase and amplitude of coherence pathways are calculated. The cost function in the optimization is $$$ \sum{_i}\sum{_j}\vert{A_j \sum{_k} e^{i(\varphi_j\cdot \Phi_k - \theta{reciever,i})}}\vert$$$, where i, j, and k are indices of the echo number, coherence pathway, and repetition of scan, respectively. Φk is a vector containing the phases of all the RF pulses in the kth repetition, and φj is a vector storing the phase dependence of the jth coherence pathway on the RF phase. θreceiver,i is the receiver phase at the ith echo time as determined by the phase of the desired coherence pathway. Aj is the amplitude of coherence pathway. The optimization was performed for each combination of the targeted echo train length and number of averages.The schemes were validated with simulation and PEPI experiments on a resolution phantom and a mouse head. The pulse sequence diagram for the 2D PEPI scheme is shown in Fig. 1, where a small amplitude and/or short duration phase encoding gradient is applied before every second echo. All experiments were performed at 1T. For the resolution phantom, the FOV was 25mm x 25mm with a 0.4mm x 0.4mm resolution and 1mm slice thickness. A 1350ms TR, 4ms TE, and 16 ETL with 4 averages were used. For the mouse head image, the FOV was 20mm x 20mm with a 0.16mm x 0.16mm resolution and 1mm slice thickness. A 975ms TR and 5ms TE with a 16 ETL was used. A scheme optimized with 10 averages was repeated 4 times for a total of 40 averages.
Results and Discussion
An example of the optimized phase cycling scheme is shown in Fig. 2. The optimized phases appear irregular. The conventional XY-162 phase cycling scheme is plotted for comparison. PEPI images were simulated with a 170° refocussing angle as shown in Fig. 3. Severe coherence pathway artifacts are observed in the phase encoding direction in each of the unaveraged images. After averaging, the artifacts are mostly removed, demonstrating the effectiveness of the phase cycling scheme.The optimized phase cycling scheme was applied in 2D slice selective PEPI experiments as in Fig. 4. In Fig. 4a-c, the proposed scheme is shown to be quite insensitive to changes in flip angle, with only low intensity coherence pathway artifacts at a nominal 160° refocussing. The conventional XY-16 method had coherence pathway artifacts even at a nominal 180°, as shown in Fig. 4d. It was much more sensitive to non-ideal refocusing. The image quality severely degraded as the flip angle decreased, as in Fig. 4e and Fig. 4f.
The scheme was applied to a 2D slice selective PEPI on a mouse head as shown in Fig. 5. The conventional XY-16 method had significant coherence pathway artifacts, distorting a large portion of the image as shown in Fig. 5b. The optimized phase cycling scheme provided a relatively artifact free image in Fig 5a, which had a similar quality to an FSE image (Fig. 5c). For the same resolution, the FSE required a maximum gradient amplitude of 164 mT/m compared to the 47 mT/m in PEPI. The FSE had a 49 times higher gradient duty cycle compared to PEPI in the phase encoding dimension. There are slight differences in the contrast, and the SNR appeared lower in PEPI. This is mostly because FSE used the relevant coherence pathways, while the phase cycling cancelled all the coherence pathways except for the primary spin echoes.
Signal averaging may generally be necessary for high resolution and/or low field imaging. The proposed method is advantageous in these applications that no extra scan time is required.
Conclusion
A phase cycling scheme has been proposed which minimizes the contribution of unwanted coherence pathways for PEPI experiments. The artifact reduction removed the perfect refocusing condition previously required by PEPI. This allows high quality slice selective 2D measurement that can be implemented in clinical and preclinical scanners to achieve high resolution imaging with low gradient amplitude and much reduced gradient duty cycle.Acknowledgements
MA thanks NSERC Canada for a CGS scholarship. DX thanks NSERC Canada for a Discovery grant.References
1. Xiao, D., & Balcom, B. J. (2015). "π Echo-Planar Imaging with concomitant field compensation for porous media MRI" Journal of Magnetic Resonance, 260, 38–45.
2. Gullion, T., Baker, B., & Conradi, M., (1990) "New, compensated Carr-Purcell sequences" Journal of Magnetic Resonance, 89, 479-484.
Figures
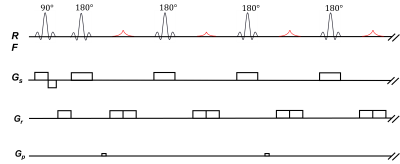
Fig. 1. 2D PEPI pulse sequence. A low amplitude and short duration of phase encoding gradient is applied before every second echo. The phase is accumulated throughout the echo train to traverse k-space.
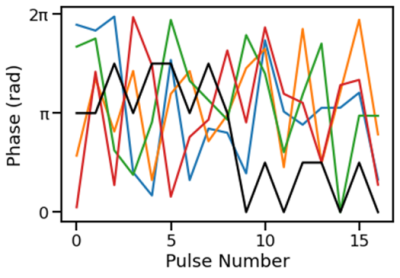
Fig. 2. An example of the optimized phase cycling scheme. Each colored line shows the RF phases of one average. The black line is the XY-16 phase cycling for comparison.

Fig. 3. Simulations of the PEPI experiment with refocusing RF pulses of 170°. (a) is the phantom. (b) shows 4 scans with refocusing RF phases as in Fig. 2, where coherence pathway artifacts are present in the phase encoding direction. The averaged image (c) had improved quality with much reduced artifacts.

Fig. 4. 2D PEPI experiments were performed on the phantom with the proposed optimized phase cycling (top row) and XY-16 phase cycling (bottom row). The optimized scheme produced artifact free images at 180° and 170°. Low intensity artifacts appeared with a nominal 160° refocusing. More severe artifacts are observed with decreasing flip angles for XY-16. The proposed scheme significantly improved image quality and robustness against non-ideal refocusing.
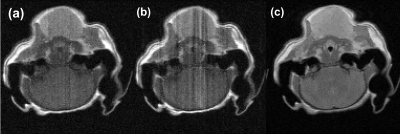
Fig. 5. 2D PEPI experiments with the optimized phase cycling (a) and XY-16 (b) are compared to an FSE image (c) of a mouse head. Coherence pathway artifacts were largely removed in (a). The phase encoding gradient duty cycle in PEPI was only 2% of FSE.
DOI: https://doi.org/10.58530/2023/2382