2372

B1+ inhomogeneity mitigation in slice-selective excitation at 7T with a single-channel RF coil augmented by ΔB0 shim array fields

Molin Zhang¹, Georgy Guryev¹, Nick Arango¹, Jason Stockmann^2,3, Jacob White¹, and Elfar Adalsteinsson^1,4,5
¹EECS, MIT, Cambridge, MA, United States, ²Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, ³Department of Radiology, Harvard Medical School, Charlestown, MA, United States, ⁴Harvard-MIT Health Sciences and Technology, MIT, Cambridge, MA, United States, ⁵5 Institute for Medical Engineering and Science, MIT, Cambridge, MA, United States

Synopsis

Keywords: Pulse Sequence Design, RF Pulse Design & Fields

We explored the utility of shim array fields in the mitigation of in-plane B1+ inhomogeneity for a slice-selective excitation at 7T and achieved better magnitude of transverse magnetization compared with birdcage transmit using conventional single-channel RF excitation. Approximately 2:1 range of B1+ was mitigated, at the cost of increased peak RF power, shim array current demands up to 20 A, and minor out-of-slice sidelobes.

Introduction

At 7T, within-slice B1+ inhomogeneity compromises SNR and contrast in diagnostic imaging with conventional single-channel RF systems. To address this, parallel transmission (pTx) [1,2,3,4] methods have been demonstrated to successfully mitigate flip angle variations due to B1+ inhomogeneity, but with additional constraints on SAR management over single-channel RF excitations.
Recent developments of independently driven multi-coil (MC) shim arrays enrich the design space by providing spatially non-linear DB0 fields [5,6]. Such arrays have been proposed and demonstrated to improve B0 shimming as well as selective excitation [7] designs. A critical tool for spatially-selective RF designs with shim arrays is a time-discrete Bloch simulator with auto-differentiation [8], which can be used to optimize both the RF pulse envelope and shim currents. Such design methods have yet to be applied to B1+ mitigation at high.
Here we explore, in simulation, the potential utility of a shim array augmenting a standard single-channel RF system for improved slice-selective excitation with B1+ inhomogeneity mitigation at 7T. The RF pulse is limited to a 4-ms duration in the presence of a constant slice-selective gradient, and a set of optimized currents to drive a large shim array of 72 coils. The B1+ inhomogeneity derives from simulations of a birdcage excitation of an adult brain at 7T. Preliminary results demonstrate successful mitigation of within-slice B1+ inhomogeneity with a range of approximately 2:1, peak-to-trough, with shim array currents under 20A, and out-of-slice ripple that’s limited to anterior peripheral regions.

Methods

As studied in previous works [7], the time-discrete Bloch simulator approximates the Bloch simulation as a sequence of rotation operators. Each rotation operator is determined by the total B0 (B0 + DB0) fields in the z direction and RF (B1x and B1y) in transverse orientation. The design is configured to simultaneously optimize the RF envelope for a 90-degree excitation as well as shim currents, given a constant slice selective gradient according to the cost function below,
$$\underset{I \in \mathbb{R}^{{n_{t}} \times {n_{\text {coil}}}}, b \in \mathbb{C}^{n_t}}{\operatorname{argmin}} \mathcal{L}=f\left(\left|\boldsymbol{M}_{x y}(I, b)\right|,\left|\boldsymbol{M}_D\right|\right)+\lambda_1 \mathcal{R}_1(I)$$
$$s.t. \begin{array}{ll} & \|b\|_{\infty} \leq b_{\max } \\& \|I\|_{\infty, \infty} \leq I_{\max } \\& \left\|\frac{d I}{d t}\right\|_{\infty, \infty} \leq s_{\max }\end{array}$$
Here, $$$f$$$ is the least-square error on magnitude; $$$I$$$ is the coil current; $$$b$$$ holds the coefficients of the birdcage transmit fields (RF=b*birdcage field); $$$n_t$$$ is the number of time point; $$$n_{coil}$$$ is the number of shim coils in the shim array; $$$M_D$$$ is the desired slice profile; $$$M_{xy}$$$ is the actual excitation profile generated by the birdcage fields and the time-varying ΔB0 fields under the time-discrete Bloch simulator; regularizes shim array currents; $$$b_{max}$$$ is the maximum coefficients; $$$I_{max}$$$ is the maximum current constraint for single coil and $$$s_{max}$$$ is the bandwidth constraint for the coil current.
We applied a stochastic offset strategy to refine the slice profile in the interval of the fixed spatial points for the optimization. For each iteration, we added a random offset to the coordinates of the points that are evaluated and optimized with the auto-differentiation. This approach promotes better adherence of the desired slice profile throughout the volume as opposed to being limited to a set of fixed points.

Results and Discussion

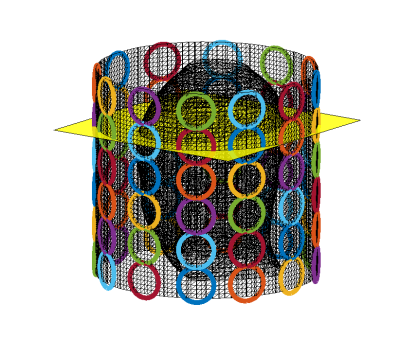
The simulated adult brain data has dimension of 40*40*50 voxels with the resolution of 5 mm. As shown in Fig.1, we heuristically place 72 coils with 4 cm diameter at the surface of a cylinder surrounding the head. The quadrature-driven birdcage fields for the adult brain were simulated using MARIE [9,10] in the CP mode.

The objective function is limited to only the magnitude of the transverse magnetization, which for each voxel is derived by a sum over 80 equally spaced sub-voxel.

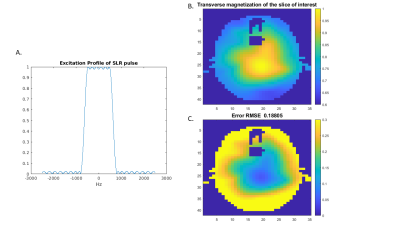
Fig. 2 B,C show the transverse magnetization of the slice of interest after applying SLR coefficients to the birdcage fields using time-discrete Bloch simulator, demonstrating an approximately 2:1 ratio of max to min values of the magnitude of field within the slice.

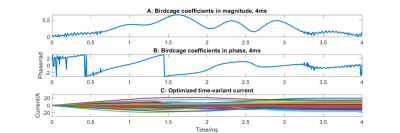
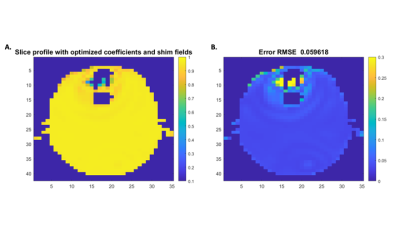
Compared with the within-slice nonuniform flip angle with the SLR waveform, the optimized RF coefficients along shim currents driving a multi-coil array, result in a more uniform transverse magnetization magnitude across the slice. Figure 3 shows the optimized coefficients waveform and phase as well as the coil current. The peak RF during the excitation process is 0.047 mT. Seen from figure 4, this method improves the magnetization profile of the slice of interest and reduces RMSE.

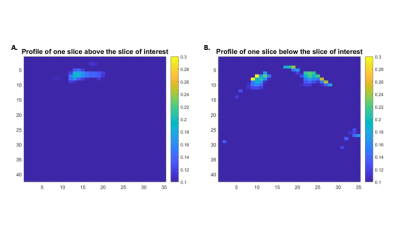
Adjacent slices, above and below the selected axial one, demonstrate a small amount of through-slice sidelobes, which are most prominent near the anterior periphery of the brain, see Fig.5. In future work, such sidelobes may be addressed by adjusting weights in cost function for different spatial regions. Future work will also implement rewinding of phase within the selected slices by application of shim array fields and gradient after the RF waveform.

Conclusion

In this work, we explored the potential usage of shim array fields in the mitigation of B1+ inhomogeneity for a slice excitation at 7T and achieved better magnitude of transverse magnetization compared with birdcage transmit using conventional single-channel RF excitation.

Acknowledgements

This research was supported by NIH R01 EB017337, U01 HD087211, R01 HD100009, and R01 EB006847.

References

1. Katscher, Ulrich, et al. "Transmit sense." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 49.1 (2003): 144-150.

2. Zhu, Yudong. "Parallel excitation with an array of transmit coils." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 51.4 (2004): 775-784.

3. Ibrahim, Tamer S., et al. "Effect of RF coil excitation on field inhomogeneity at ultra high fields: a field optimized TEM resonator." Magnetic resonance imaging 19.10 (2001): 1339-1347.

4. Setsompop, Kawin, et al. "Slice‐selective RF pulses for in vivo B inhomogeneity mitigation at 7 tesla using parallel RF excitation with a 16‐element coil." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 60.6 (2008): 1422-1432.

5. Stockmann, Jason P., et al. "A 32‐channel combined RF and B0 shim array for 3T brain imaging." Magnetic resonance in medicine 75.1 (2016): 441-451.

6. Truong TK, Darnell D, Song AW. Integrated RF/shim coil array for parallel reception and localized B0 shimming in the human brain. Neuroimage 2014;103:235–240.

7. Zhang, Molin, et al. "Selective RF excitation designs enabled by time‐varying spatially non‐linear Δ B 0 fields with applications in fetal MRI." Magnetic Resonance in Medicine 87.5 (2022): 2161-2177.

8. Luo, Tianrui, et al. "Joint Design of RF and gradient waveforms via auto-differentiation for 3D tailored excitation in MRI." IEEE Transactions on Medical Imaging 40.12 (2021): 3305-3314.

9. Villena, Jorge Fernández, et al. "Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods." IEEE Transactions on Biomedical Engineering 63.11 (2016): 2250-2261.

10. Guryev, G. D., et al. "Fast full-wave patient-specific field simulations in seconds with MARIE 2.0" ISMRM 2022.

Figures

Figure 1: The simulated adult head and shim coils used in our work. The resolution is 5mm and 72 coils with 4mm diameter are heuristically and symmetrically placed at the surface of a cylinder covering the adult brain. The yellow slice represents the slice of interest to be excited in this work.

Figure 2: (A). The excitation profile with uniform B1+ of the SLR waveform. (B). The excitation profile of the slice of interest under 7T using the SLR waveform as coefficients of the birdcage transmit field. (C). The RMSE between the transverse magnitude excitation magnetization of the slice of interest and the target.

Figure 3. (A). Optimized birdcage coefficients in magnitude. Note that during the excitation process, the peak B1 is 0.047 mT. (B). Optimized birdcage coefficients in phase. (C). Optimized shim current. The maximum current is less than 20A.

Figure 4. (A). The transverse magnitude magnetization of the slice of interest with our optimized birdcage coefficients and shim fields. (B). The RMSE between the excitation profile of the slice of interest and the target.

Figure 5. The leakage introduced by the shim fields. (A). The transverse magnitude magnetization of the slice above the slice of interest. (B). The excitation profile of the slice below the slice of interest. There are through-slice sidelobes near the edge of the adult brain.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

2372

DOI: https://doi.org/10.58530/2023/2372