Synopsis

Keywords: MR Fingerprinting/Synthetic MR, Image Reconstruction, Prostate

Magnetic Resonance Fingerprinting (MRF) is a technology that computes T1, T2 parameters from time-evaluated signals. However, long scanning time in obtaining fully-sampled data is a challenging point while reducing the sampling rate results in poor reconstructed data quality. Here, we propose a spatio-temporal deep learning network for reconstruction from the under-sampled MRF data. According to the retrospective reconstructed results, the proposed method could produce the T1 and T2 maps of high fidelity similar to the fully-sampled ground-truth.

INTRODUCTION

Magnetic Resonance Fingerprinting (MRF) opened a new horizon for Magnetic Resonance Imaging technology by obtaining quantitative T1 and T2 maps ^1,2. However, acquiring fully-sampled data of MRF has difficulties because of long scan time and under-sampled data with noise/artifact for matching causes high variance in MRF dictionary matching ^3,4. In this study, we propose a neural network for reconstruction of accelerated MRF prostate data by applying a spatio-temporal strategy ⁵. This network could correct residual artifacts and improved image quality, also T1 and T2 maps were successfully matched with dictionary from the reconstructed MRF data.

METHODS

[Data Acquisition]
3D MRF prostate data for this study were acquired using a combination of radial and echo-planar imaging (EPI) trajectory ⁶. Golden-angle rotation was applied to acquire 16 spokes (16-spk) and for slice encoding, EPI acquisition was used. Along the time axis, sinusoidal flip angle was applied over 320 measurements. Detailed image acquisition parameters were as follows: field of view (FOV) = 160 mm × 160 mm × 72 mm, resolution = 0.6 mm × 0.6 mm × 3mm, 20 coils, TR = 16 ms, total scan time = 3:48 minutes.
[Data augmentation & Dictionary]
Due to the insufficient amount of data, we augmented the under-sampled dataset (8-spk). Specifically, fully-sampled data were randomly divided into two 8-spk four datasets. The images reconstructed from the 8-spk data were put into the network for training, and the average of two 8-spk images (NEX = 2) from each set were treated as label.
Dictionary was simulated for 320-time measurements using different set of T1 and T2 parameters. The range for T1 was from 50 ms to 4000 ms and T2 ranged from 5 ms to 400 ms. The dictionary of 320-time measurements with 91,811 entries was compressed into 5 singular points in temporal domain using singular value decomposition (SVD).
[Reconstruction process]
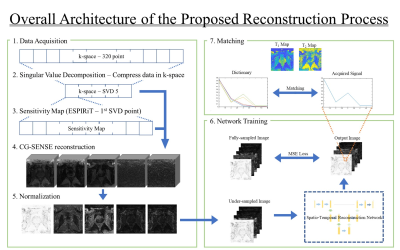
Figure 1 shows the overall architecture of the reconstruction process. To reduce the reconstruction computation burden, we applied SVD to compress the -space data from 320-time measurements to 5 singular points. The sensitivity maps for coil combined images were computed from the first singular image via ESPIRiT technique ⁷. Using the estimated sensitivity maps, the images were reconstructed with conjugate gradient SENSE (CG-SENSE) ⁸. We utilized BART Toolbox ⁹ to apply both ESPIRiT technique and CG-SENSE reconstruction. We normalized the singular vector images with L2-norm for each vector.
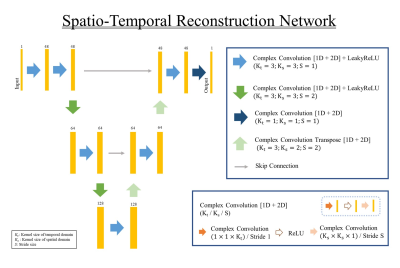
The architecture of the proposed network is provided in Fig 2. The proposed network takes 3D complex MRF images, the stack of 5 singular images from MRF, as an input. The basic structure of the network is based on the U-Net ¹⁰. To remain both magnitude and phase information of the image, all convolution layers in the network perform the complex convolution. To compensate both spatial images and temporal components, we utilized 2D + t spatio-temporal reconstruction. To apply spatio-temporal convolutions, we constructed the convolution layers with two separate complex convolution sub-layers. After the images were reconstructed, we produced the parameter map for T1 and T2 values using the reconstructed signal evolution and predefined MRF dictionary. For matching T1 and T2 values with dictionary, the complex inner product was applied.

RESULTS

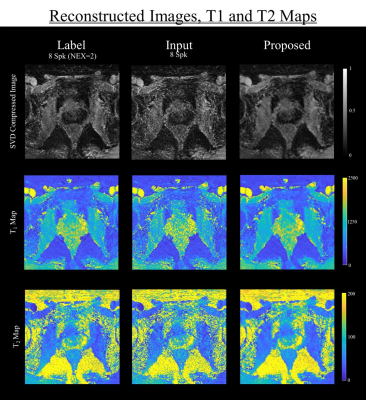
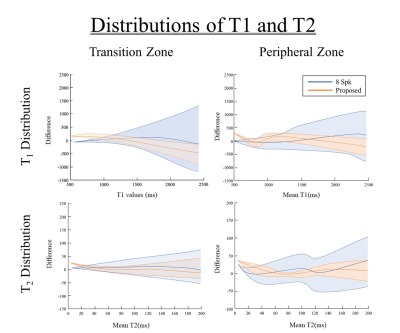
Figure 3 shows the result of reconstructed images of three data (average 8-spk images (NEX = 2), 8-spk images and the proposed result) and illustrates the comparison of SVD compressed images, T1 map and T2 map. The proposed method showed less degradation in reconstructed images compared to 8-spk images.
Figure 4 shows the distribution tendency of T1, T2 values of two major prostate areas, transition zone (TZ) and peripheral zone (PZ). The figure illustrates the difference of T1, T2 values between 8-spk image, the results reconstructed by proposed method with label, respectively. In the graphs, mean and standard deviation of the differences are represented with solid and dotted lines. Qualitatively, the proposed method shows smaller variance in both regions than 8-spk images.

DISCUSSION AND CONCLUSION

In this study, we proposed a spatio-temporal reconstruction network for accelerating the reconstruction of MRF prostate data. By exploiting 2D + t spatio-temporal convolution layer, the proposed network can focus on the compressed time signal evaluation of each pixel, which is the key component of MRF. Allowing the network to concentrate only on time and image domain separately, the result showed the low variance of T1, T2 values. Also, spatio-temporal convolution layers have additional nonlinear rectification, compared to 3D convolution. This increases the capability of the network to represent more complex functions ¹¹. We demonstrated the acquisition accurate T1, T2 maps from under-sampled with accelerated reconstruction. This indicates the possibility of reducing the total scan time of MRF. Also, the complex inner product used in this study is one of the simplest algorithms for dictionary matching. This implies that the matching process is not optimized for the given data. Therefore, improving the matching technique using deep learning network suggests the potential for performance enhancement in future study.

Acknowledgements

This research was supported by the MSIT(Ministry of Science and ICT), Korea, under the ITRC(Information Technology Research Center) support program(IITP-2020-2020-0-01461) supervised by the IITP(Institute for Information & communications Technology Planning & Evaluation).