2205
Phase-based T2 mapping using dual phase-cycled balanced SSFP imaging
Merijn Berendsen1, Maša Bozic-Iven1,2, Joao Tourais1, Chiara Coletti1, Ingo Hermann1,2, and Sebastian Weingärtner1
1Delft University of Technology (TU Delft), Delft, Netherlands, 2Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany
1Delft University of Technology (TU Delft), Delft, Netherlands, 2Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany
Synopsis
Keywords: Pulse Sequence Design, Pulse Sequence Design
Phased-based techniques have shown promise for scan time efficient quantification of T2 relaxation times. However, previously proposed methods use an unbalanced Gradient Echo approach, which shows residual sensitivity to B1+ and T1 changes. In this work, a dual phase-cycled balanced SSFP approach is proposed. Simulations and phantom measurements show its resilience against field inhomogeneities. Excellent agreement between phase values was obtained in phantom and simulations. Initial phantom acquisitions at 3T yield T2 maps with visually high map quality and close agreement to a spin-echo reference. Future evaluation of in vivo robustness and inter- and intra-subject repeatability is warranted.Introduction
With the emergence of fast pulse sequences, quantification of tissue relaxation times is increasingly gaining interest, due to its promise of inter- and intra-subject comparability. Recently, phase-based techniques have been proposed as a scan time efficient quantification method, where the T2 information is encoded in the signal phase of a steady state acquisition2. Wang et al.2 described phase-based T2 mapping using small quadratic RF phase increments in an unbalanced gradient echo (GRE) sequence. This enabled scan time efficient imaging, albeit with residual sensitivity to T1 and confounding effects of B1+ inhomogeneities. Here, we propose a novel approach for phase-based T2 mapping using balanced sequence designs. Sensitivity and various confounders are evaluated in simulations and initial feasibility is demonstrated in phantom scans at 3T.Methods
In contrast to previous methods for phase-based T2 mapping, we suggest using a balanced sequence design based on the balanced Steady State Free Precession (bSSFP) technique (Fig 1). Due to its spin-echo character, the signal phase is independent of the T2 time, but T2 phase dependence emerges when phase-cycling is used. To minimize off-resonance dependence, we propose to use a dual phase-cycled bSSFP approach with symmetric phase increments of Δɸ=±90°.Using extended phase graph (EPG) simulations3, the proposed approach was compared to phase-based T2 mapping using unbalanced GRE with small quadratic phase increments (ѰA=2°)2. Magnetization evolution towards the steady state, as well as T1, T2, and B1+ dependence of the phase signal was assessed. Additionally, quantification with the proposed dual phase-cycled bSSFP using different TRs was tested for off-resonance effects.
Phantom imaging (NIST/ISMRM4) was performed at 3T (Ingenia, Philips) with the following sequence parameters: Resolution: 0.8x0.8mm2, Slice Thickness: 8mm, FOV: 400x400mm2, Flip Angle (FA): 18°, TR/TE = 4.0/2.0ms. T2 maps were generated by matching the measured phase difference to the EPG simulations. Resilience against B1+ and B0 inhomogeneities was studied by varying the FA between 2 and 30° and the offset frequency between -100 to +100Hz. Precision is evaluated as the coefficient of variability (CoV) within a manually drawn ROI. Accuracy is assessed in comparison to reference T2 maps acquired with a CPMG sequence with 8 echos and 15ms echo spacing.
Results
As shown in Fig 1, dual phase-cycled bSSFP shows a slower approach to steady-state, with pronounced ripples, when compared to conventional bSSFP. However, compared with unbalanced GRE, the steady state is reached faster, and with a more regular magnitude and phase pattern.Fig 2 shows the signal phase for the different methods as a function of T2, T1, and FA. Both unbalanced GRE and dual phase-cycled bSSFP show strong dependence on the T2 time, with a diminishing trend for T2>50ms. Unbalanced GRE shows residual T1 effects, particularly for short T1<500ms, while for dual phase-cycled bSSFP no T1 effect is observed. Similarly, changes in the FA introduce spurious phase changes for the unbalanced GRE approach, while the dual phase-cycled bSSFP phase is independent of the FA.
In dual phase-cycled bSSFP off-resonance effects are more pronounced for longer T2 times and longer TR (Fig 3). For TR of 4ms and T2 of 45ms ±17.6Hz off-resonance can be tolerated for less than 10% error in T2, but increased tolerance is seen for lower TR.
In phantom, a largely homogenous phase pattern was observed in the dual phase-cycled bSSFP approach. No significant trend of the phase difference is observed in different vials as a function of the FA (Fig. 5, R2=0.33). Phantom T2 maps acquired at different off-resonances were in good agreement with the simulations, showing a similar off-resonance plateau.
The phase difference between the two phase-cycled acquisitions showed excellent agreement with the simulations. T2 maps derived from the phase difference show visually homogenous quantification, with an excellent agreement with the reference maps (T2 error between -2.6ms and 2.2ms). Good precision is achieved for T2 times up to 50ms (CoV<6.6%) and increased variability for vials up to 100ms (CoV<11.8%).
Discussion
A dual phase-cycled bSSFP sequence for phase-based T2 mapping was evaluated and showed good resilience against T1 and FA changes. Proof-of-principle phantom imaging showed excellent agreement with numerical simulations and yielded visually homogenous T2 maps.Underestimation of the T2 time can be observed due to residual off-resonance sensitivity of the dual phase-cycled bSSFP sequence. B0 maps can be acquired to account for the off-resonance in the reconstruction. Additionally, shorter TRs can be used to reduce both the off-resonance and scan time, at the expense of reduced T2 sensitivity. Thus, careful parameter selection is warranted to minimize off-resonance sensitivity while maintaining sufficient noise resilience in the T2 maps.
Initial evaluation in phantoms demonstrated excellent agreement with the phase values predicted from the EPG simulations. This yielded visually homogenous quantification of T2 times up to 100ms. Future in vivo evaluation is warranted to study the feasibility of the proposed method in vivo, either at 3T or 1.5T, where off-resonance effects are reduced.
Conclusion
Dual phase-cycled bSSFP imaging was proposed for phase-based T2 mapping. Initial proof-of-principle measurements show excellent agreement between phase values obtained in phantom and simulations, leading to T2 maps with high visual map quality and accuracy.Acknowledgements
S.W. acknowledges funding from the 4TU Precision Medicine program, an NWO Start-up STU.019.024, and ZonMW OffRoad 04510011910073.References
- Gracien RM, Maiworm M, Bruche N, Shrestha M, Noth U, Hattingen E, Wagner M, Deichmann R. How stable is quantitative MRI? - Assessment of intra- and inter-scanner-model reproducibility using identical acquisition sequences and data analysis programs. Neuroimage 2020;207:116364.
- Wang, X., Hernando, D., & Reeder, S. B. (2020). Phase-based T2 mapping with gradient echo imaging. Magnetic resonance in medicine, 84(2), 609–619. https://doi.org/10.1002/mrm.28138
- Weigel, Matthias. (2015). Extended Phase Graphs: Dephasing, RF Pulses, and Echoes - Pure and Simple. Journal of magnetic resonance imaging : JMRI. 41. 10.1002/jmri.24619.
- Russek SE, Boss M, Jackson EF, Jennings DL, Evelhoch JL, Gunter JL, Sorensen AG. Characterization of NIST/ISMRM MRI system phantom. In Proceedings of the 20th Annual Meeting of ISMRM, Melbourne, Austraia, 2012. Abstract 2456.
Figures
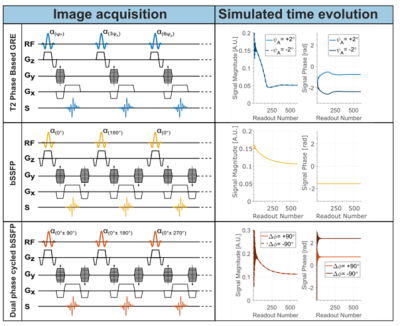
Figure 1: Pulse sequence diagram (left) and signal magnitude and phase over time (right) for T2 phase-based unbalanced gradient echo (top), balanced SSFP (middle), and dual phase-cycled balanced SSFP (bottom). Quadratic phase increments are represented with ѰA, and symmetric phase increments with Δɸ. In the simulated signal evolution, the following parameters were used: FA=18°, TR=4ms, T2=50ms, and T1=1000ms.
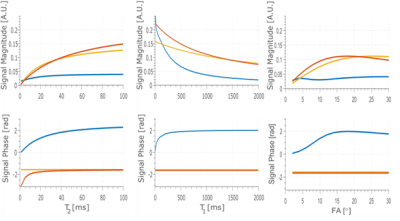
Figure 2: Simulated signal magnitude (top row) and phase (bottom row) over a range of T1 (left), T2 (middle), and flip angle (FA) (right) for unbalanced gradient echo (blue), balanced SSFP (yellow), and dual phase-cycled bSSFP (orange). The proposed dual phase-cycled bSSFP approach shows a strong dependence on the T2 time, while no T1 or FA dependence is observed.
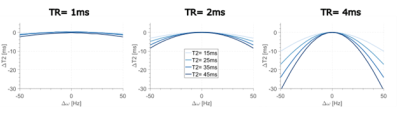
Figure 3: Simulated variation of T2 values (ΔT2) over a range of off-resonance values (Δ⍵) for the proposed dual phase-cycled bSSFP approach using a TR of 1ms (left), 2ms (middle) and 4ms (right). Four different T2 values, ranging from 15 to 45ms are shown. Signal was generated using T1=1000ms and Flip Angle=18°.

Figure 4: Phantom experiment results of the proposed dual phase-cycled bSSFP approach using a TR of 4ms. On the left is the reconstructed signal phase of the positive (top) and the negative (bottom) cycled sequence. In the middle is the phase difference between the aforementioned signals and on the right is the T2 map estimate (top) and the reference T2 map (bottom).

Figure 5: Signal phase over a range of off-resonance (left) and flip angle (FA) (right) for each T2 measurement in the phantom containers using the proposed dual phase-cycled balanced SSFP sequence. The same TR=4ms was used for both experiments and a fixed FA=18° was used in the off-resonance measurements (left).
DOI: https://doi.org/10.58530/2023/2205