2204
Unsupervised Learning-based Pulse Sequence Optimization framework for Magnetic Resonance Fingerprinting
Peng Li1, Yinghao Zhang1, Xin Lu2, and Yue Hu1
1Harbin Institute of Technology, Harbin, China, 2De Montfort University, Leicester, United Kingdom
1Harbin Institute of Technology, Harbin, China, 2De Montfort University, Leicester, United Kingdom
Synopsis
Keywords: Pulse Sequence Design, MR Fingerprinting
The optimal design of the Magnetic resonance fingerprinting (MRF) sequence is still challenging due to the optimization of high-degrees-of-freedom acquisition parameters. In this paper, we propose a novel unsupervised learning-based pulse sequence design framework for efficient MRF sequence optimization. Specifically, we propose a novel pulse sequence generation network (PSG-Net) that fully exploits the sequence correlation to generate the optimal pulse sequence from a zero-initialized input. To achieve improved precision of parameter estimation, we use a predefined pulse sequence performance evaluation function that can directly represent tissue quantification separability as the loss function to update the parameters of the PSG-Net.Introduction
Magnetic resonance fingerprinting (MRF) is a quantitative MRI framework recently proposed by Ma et al.[1], which can rapidly perform simultaneous imaging of multiple tissue parameters such as proton density ($$$\rm PD$$$), spin-lattice relaxation time ($$${\rm T}_1$$$), and spin-spin relaxation time ($$${\rm T}_2$$$). The pulse sequence used in MRF[2] achieves the discrimination of tissues by simultaneously varying sequence parameters, which can lead to unique signal evolution for each tissue. Subsequently, the quantification parameters are obtained by mapping each tissue signal to a dictionary containing theoretical signal responses from all tissues. Thus, the pulse sequence used in MRF directly determines the uniqueness [3] and separability of the acquired tissue signal, which in turn affects the accuracy of parameter estimation. The reconstruction accuracy of the parameter maps and the data acquisition efficiency highly depends on the predefined MRF pulse sequences. However, the optimal design of the MRF sequence is still challenging due to the optimization of a large number of degrees of freedom of the acquisition parameters.Several studies have been devoted to simplifying sequence design problems based on MRF imaging models and mathematical models. Zhao et al.[4] optimized the sequence parameters by estimating lower bounds on the variance of the $$${\rm T}_1$$$ and $$${\rm T}_2$$$ parameter estimates in MRF based on the Cramer-Rao bound. Jodan et al.[5] proposed a cost function based on parameter estimation error and a physics-inspired optimization algorithm to perform sequence optimization from randomly generated inputs. However, the optimization problem based on the simplified model leads to a cost function with high computational complexity. As a result, the above methods usually performed pulse sequence optimization with a limited number of typical tissue parameters, and the resulting optimized sequences may lack generalizability.
Methods
Traditional supervised deep learning techniques cannot be directly applied to the optimal design of MRF due to the lack of reference data. Unsupervised learning can learn patterns from untagged data, providing a basis for pulse sequence optimization. An unsupervised network mimics specific data and uses the error in its mimicked data to correct itself, usually relying on a specially designed network and an evaluation function of the generated data. A suitable network can reduce the generated data space, and an accurate evaluation function can better measure the quantification error and thus adjust the parameters of the network. Fig.1 shows an overview of the proposed unsupervised learning-based pulse sequence optimization framework. The PSG-Net first generates a pulse sequence from a zero-initialized input. Then, the proposed performance evaluation function is used as a loss function to evaluate the generated pulse sequence and update the parameters of the PSG-Net. The above process is repeated iteratively until the evaluation function converges, obtaining the optimal pulse sequence. Fig.2 illustrates the structure of the proposed pulse sequence generation network (PSG-Net). Note that the number of PSG cells is the length of the target pulse sequence. The proposed pulse sequence performance evaluation function can be modeled as:$$ \min_\theta \lVert \mathbf{W}\!\cdot\! \hat{\mathbf{D}}\hat{\mathbf{D}}^T -\mathbf{I} \rVert_2^2 $$
where $$$\hat{\mathbf{D}}$$$ represents the dictionary consisting of all normalized entries and $$$\mathbf{I}$$$ is the unit diagonal matrix. $$$\mathbf{W}$$$ is the proposed weight focusing matrix, imposing higher penalty weights on similar entries. One way to estimate and update the weight-focusing matrix is: $$$ \mathbf{W}_{n}=\lvert\hat{\mathbf{D}}_{n-1}\hat{\mathbf{D}}^T_{n-1}\rvert^2$$$, where $\hat{\mathbf{D}}_{n-1}$ represents the dictionary built by the generated parameter sequence in the last iteration.
Results and discussion
The Bloch simulations used in the experiments were based on the FISP pulse sequence[2]. The dictionary was generated according to [6]. The length of the sequence is set to 500. The parameters of the smoothing module in the network have a value range of $$$(0, 0.1]$$$ for FA and a value range of $$$(0, 0.5]$$$ for TR.Fig.3 shows the pulse sequence parameters evolution used in [2] and the parameters evolution generated by the proposed PSG Net. To quantitatively compare the performance of different sequences, we calculated the normalized correlation value $$$c$$$ between all entries in the generated dictionary, which can be expressed as: $$$c^{i}=|\langle \hat{\mathbf{d}}_{i,:}, \hat{\mathbf{d}_{j}}\rangle |$, $1 \leq i,j \leq M$$$.We then calculated the distribution of the correlation value $$$c$$$, as shown in Fig.4. The statistical results show that the sequences optimized by the proposed framework can effectively reduce the correlation between highly correlated entries. To further verify the performance of the parameter evolution generated by our proposed PSG Net, we conducted experiments on simulated data using known quantitative parameters, as shown in Fig.5. To quantitatively evaluate the experimental results, we computed the normalized mean square error (NMSE) between the reference and the estimated parameters map. Experimental results show that the signal evolution generated by our proposed network can improve the accuracy of parameter estimation under the same experimental conditions compared to the originally used pulse sequence evolution.
Conclusion
We proposed a novel unsupervised learning-based pulse sequence design framework for efficient MRF sequence optimization without reference data. We proposed a novel pulse sequence generation network (PSG-Net) to generate the optimal pulse sequence from a zero-initialized input. To achieve improved precision of parameter estimation, we proposed an imaging mechanism-inspired pulse sequence performance evaluation function to update the parameters of the PSG-Net according to the generated pulse sequence.Acknowledgements
This work is supported by China NSFC 61871159 and Natural Science Foundation of Heilongjiang YQ2021F005.References
- Dan Ma, Vikas Gulani, and et al., “Magnetic resonancefingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192,2013.
- Yun Jiang, Dan Ma, and et al., “MR fingerprinting usingfast imaging with steady state precession (FISP) withspiral readout,” Magnetic resonance in medicine, vol. 74,no. 6, pp. 1621–1631, 2015.
- Charit Tippareddy, Walter Zhao, and et al., “Magneticresonance fingerprinting: an overview,” European Journalof Nuclear Medicine and Molecular Imaging, pp. 1–12, 2021.
- Bo Zhao, Justin P Haldar, and et al., “Optimal experimentdesign for magnetic resonance fingerprinting: Cramer-Rao bound meets spin dynamics,” IEEE transactions onmedical imaging, vol. 38, no. 3, pp. 844–861, 2018.
- Stephen P Jordan, Siyuan Hu, and et al., “Automateddesign of pulse sequences for magnetic resonance fingerprintingusing physics-inspired optimization,” Proceedingsof the National Academy of Sciences, vol. 118, no.40, 2021.
- Yue Hu, Peng Li, and et al., “High-Quality MR FingerprintingReconstruction Using Structured Low-RankMatrix Completion and Subspace Projection,” IEEETransactions on Medical Imaging, vol. 41, no. 5, pp.1150–1164, 2021.
Figures
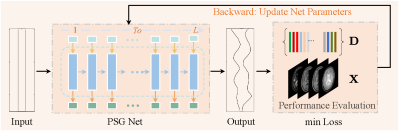
Fig.1 Overview of the proposed unsupervised learning-based optimal pulse sequence optimization framework.
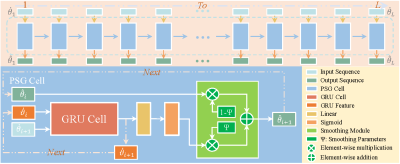
Fig.2 Illustration of the proposed Pulse Sequence Generation Network (PSG-Net).
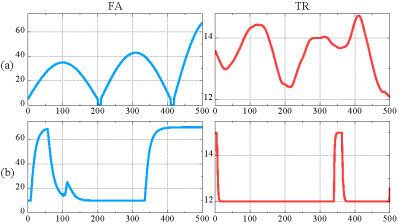
Fig.3 Illustration of the generated pulse sequence parameters evolution. (a) represent the FA and TR parameter evolutions used in [2]. (b) are the FA and TR parameter evolutions generated by our proposed PSG-Net.
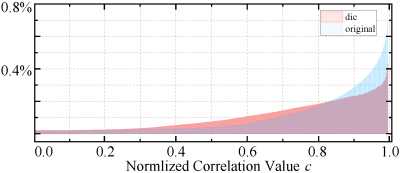
Fig.4 Illustration of the correlation value $c$ statistical results. Similar to histogram statistics, the horizontal axis represents the normalized correlation value $c$, and the vertical axis represents the percentage of occurrences.
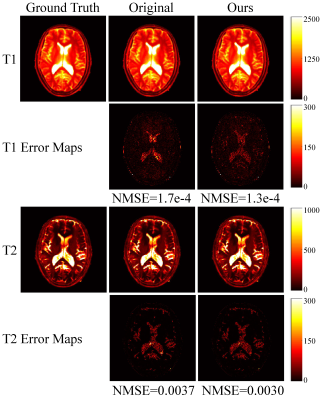
Fig.5 The experimental results (${\rm T}_1$ and ${\rm T}_2$) were obtained using different pulse sequence evolutions with fully sampled noise-contaminated data.
DOI: https://doi.org/10.58530/2023/2204