Synopsis

Keywords: Data Analysis, High-Field MRI, phase-cycled bSSFP, Aceton fraction quantification

A novel Off-Resonant encoded Analytical parameter quantification using Complex Linearized Equations (ORACLE) method using phase-cycled bSSFP profiles was developed. The approach decodes complex asymmetry profiles in multi-compartment systems for simultaneous proton fraction, T₁/T₂ ratio, T₁ and T₂ quantification. The approach was validated in simulations and in an acetone-water phantom at 3T and 7T. Simulations and experiments validated the proposed method for multi-parameter quantification using phase-cycled bSSFP for two compartment singlet systems with high accuracy and precision. This provides the first step towards proton fraction quantification of more complex multiplet-systems, such as fat or myelin, exploiting complex asymmetry profiles.

Introduction

Phase-cycled (PC) balanced-steady-state free-precession (bSSFP) acquisitions have traditionally been used to remove banding artifacts, but more recently for multi-parameter quantification in single-compartment systems [1-4]. Current approaches correct off-resonance effects by dismissing valuable parts of the phase-information [2,3,4], and do not utilize the phase to its full extent, hampering the extension to multi-compartment systems. Asymmetries observed in the PC-bSSFP profile have been used to quantify water and fat [5], however, to coherently describe constructive and destructive interference, multiple off-resonance sources need to be analytically disentangled. This work aims to develop an analytical framework for proton-fraction quantification of two-compartment singlet-systems with PC-bSSFP signal-profiles, while also providing banding artifact-free images. The method was validated on acetone-water mixtures at 3T and 7T

Methods

PC-bSSFP Fourier-space
For independent $$$T_1$$$, $$$T_2$$$ and proton-fraction quantification the use of complex data is neccesary. Because the signal-evolution over the PC-dimension $$$\varphi$$$ is sensitive to off-resonance effects, inverting the signal to quantify parameters is challenging. For multi-compartment systems, the phases and magnitudes follow complicated dynamics, and their robust disentanglement remains an unsolved mathematical problem [6]. The problem can be simplified and better-conditioned by transforming the signal $$$S(\varphi)$$$ into Fourier-space [3,4]:
$$c_n=\sum_{j=0}^{N-1}S(\varphi_j)\cdot\text{e}^{\text{i}\,n\,\varphi_j}\,,\quad \varphi_j=\frac{2\pi}{N}\cdot j \;,\quad j=[0,N-1]\,,$$
where $$$N$$$ is the number of phase-cycles and $$$c_n$$$ is the $$$\text{n}^{\text{th}}$$$-mode.
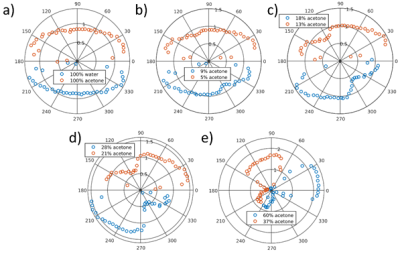
For periodic PC-bSSFP-profiles the main advantage of Fourier-transformations is the compression of almost all information in the center of the Fourier-mode-space similar to the relation between k-space and image-space (Figure 1 a,b).
Fraction estimation
In this work we used the analytical solution of $$$c_{-2}$$$, $$$c_{-1}$$$, $$$c_0$$$ and $$$c_2$$$ modes in dependence of an input-value $$$\Delta\phi_1=\gamma B_0\Delta\delta\text{TR}$$$, with $$$\gamma$$$ the gyromagnetic-ratio, $$$B_0$$$ the main magnetic-field, $$$\text{TR}$$$ the repetition-time and $$$\Delta \delta$$$ the chemical-shift difference of both substances. When using a correctly defined $$$\Delta\phi_1$$$ , the solutions predict the values of every other mode of the experimental bSSFP profile (Figure 1b). We conjecture that the minimum of the sum-of-squares of absolute-difference between predicted and experimental modes result in a good point-estimation for the proton-fraction, $$$T_1$$$ and $$$T_2$$$.
Simulations and Experiments
Simulations: To define an optimal configuration (‘bSSFP signal shape’) for fraction estimation, Monte-Carlo Bloch-equation simulations were performed for PC-bSSFP (500 variations for each value) with an SNR of 35 for $$$T_1=500\text{ms}$$$, $$$T_2=400\text{ms}$$$, $$$N=36$$$, $$$\alpha=15^\circ$$$ and $$$\text{TR}=5\text{ms}$$$ was used. Variations were performed for fractions of $$$f=[0,50]\%$$$ in 50 equidistant steps and $$$\Delta\phi_1=[0,2\pi[$$$ in 360 equidistant steps. The root-mean-square-error of $$$f$$$ was determined and plotted over initial $$$f$$$ and $$$\Delta \phi_1$$$ values.
Phantom-experiments: A PC-bSSFP experiment on an acetone-water phantom with different acetone:water ratios doped with CuCl and Gd-DOTA were performed at 3T (PRISMA, Siemens Healthineers) with $$$\text{TR}=5.00\text{ms}$$$, $$$N=36$$$, $$$\alpha=35^\circ$$$, BW=625kHz and (1mm)³ resolution. At 7T (TERRA, Siemens Healthineers) with $$$\text{TR}=3.45\text{ms}$$$, $$$N=18$$$, $$$\alpha=25^\circ$$$, BW=875kHz and (2mm)³ resolution. For the 7T-experiment the 60% acetone-vial was replaced by a 58% acetone-vial without contrast-agents, due to precipitations in the mixture. Acetone reference volumes were translated by factor 0.74 for proton-fraction reference-values to consider the lower proton-density per volume ratios of acetone w.r.t. water [7]. Both fraction-estimations for the different main-field were fixed to $$$\Delta\delta=[2.45\pm0.05]\text{ppm}$$$ [7] between water and acetone as a boundary-condition with some tolerance for complex noise and $$$B_0$$$-drift. For accuracy the coefficient-of-determination ($$$R^2$$$) w.r.t. the reference was calculated, and for precision the coefficient-of-variation (COV) or the standard-deviation ($$$\sigma$$$) within one ROI. To correct for banding an exemplary $$$\big|\frac{c_1}{c_0}\big|$$$-weighting mapped to single-compartment modes of 3T and 7T was performed as well as sum-of-squares.

Results

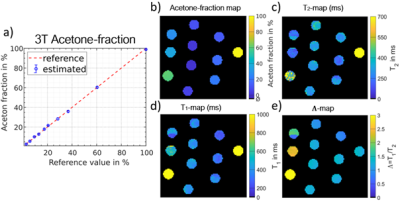
Proton-fraction quantification exhibit high accuracy ($$$R^2$$$) and precision ($$$\bar{\sigma}$$$) for 3T as well as 7T if a $$$\text{mod}(\Delta\phi_1,2\pi)\sim\pi$$$ configuration is achieved (Figure 1c). The novel fraction-quantification exhibits high robustness against noise, as low as SNR=35. For optimal configurations the fraction-estimation error is below 1.5%.
At 3T asymmetry-profiles can be observed in the acetone water fraction phantom, whose asymmetry increases the closer to a 50% proton-fraction the signal corresponds (Figure 2). The estimated fractions are in high agreement with the reference values, with coefficient-of-determination $$$R^2=0.999$$$ and averaged standard-deviation $$$\bar{\sigma}=0.60\%$$$ proton-fraction (Figure 3). $$$T_1$$$-, $$$T_2$$$- and $$$\Lambda$$$-maps are in a plausible range.
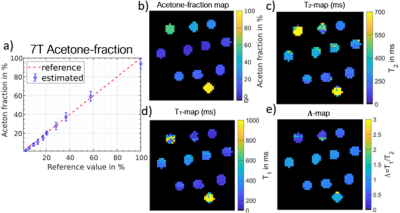
At 7T (Figure 4) all maps where masked for chemical-shift artifacts, which are more dominant at 7T. $$$T_1$$$-, $$$T_2$$$- and $$$\Lambda$$$-maps are slightly different to 3T. Fraction-maps at 7T results in $$$R^2=0.993$$$ and $$$\bar{\sigma}=2.9\%$$$ proton-fraction. Figure 5 shows bSSFP banding-artifacts compared to exemplary $$$\big|\frac{c_1}{c_0}\big|$$$-weighting mapped to single compartment modes.

Discussion

As expected, $$$T_1$$$, $$$T_2$$$ and $$$\Lambda$$$-maps are slightly different for the 3T and 7T [8]. Increased standard-deviations of proton-fraction estimation at 7T can be explained by the reduced number of phase-cycle incremented bSSFP acquisitions. Moreover, the replaced 60% acetone-vial with an 58% acetone-vial without contrast-agents shows a significant change of $$$T_2$$$-value between 3T and 7T experiment, which may indicate potential for $$$T_2$$$-quantification for two-compartment systems. Finally, mode-weighting can be used for multiple realizations of contrasts-settings, correcting for banding-artifacts for two-compartment systems.

Conclusion

A novel mathematical framework was developed that describes multi-compartment systems and asymmetries in PC-bSSFP signal-profiles. ORACLE disentangles multiple off-resonance sources such as chemical-shifts, $$$B_0$$$-inhomogeneities and additional phase offsets. ORACLE quantified proton-fractions in water and acetone at 3T and 7T.

Acknowledgements

We would like to thank Prof. Roland Kreis for suggesting acetone as a suitable substance for two-compartment singlet-system when mixed with water. This study was supported by the Swiss National Science Foundation (grant number PCEFP2_194296).