Introduction

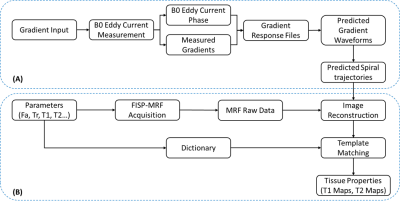
The MRF[1-4] is a highly efficient framework for MRI acquisition and reconstruction that can simultaneously provide quantitative tissue properties in one single scan. Compared with 3T, 5T MRF faces many challenges. Due to the increase of field strength, the Spiral MRF sensitive to B0 field inevitably produces artifacts. In addition, the clinical MRF needs to scan the whole body under 5T, and a universal and fast way to correct the artifacts generated by B0 eddy current is required. At present, several studies suggest that the gradient system response function[5-8] be used to mitigate the artifacts of the spiral. Although these methods have made progress in the research of EPI[6], [7] or TSE[8] based Spiral, the research of FISP based MRF Spiral remains unknown. In this study, we provide a correction technique of B0 eddy currents to mitigate the artifacts of B0 field on Spiral MRF. The in vivo experiments on the head and abdomen showed that our method was effective in reducing artifacts.

Methods

In this work, we described the measurement of B0 eddy currents with measured signal phase[9], [10] at position $$$ p $$$ and time $$$ t $$$ as: $$ \phi_{p_{0}}(t)=\hat{k}(t) p_{0}+\phi_{B_{0}}(t)+\Delta \omega_{0}\left(p_{0}\right) t+\phi_{C}\left(p_{0}, t\right) $$ where $$$\hat{k}(t)$$$ is the actual location, $$$\phi_{B_{0}}$$$ is the B0 eddy current phase, $$$\Delta \omega_{0}$$$ is the susceptibility‐induced off‐resonance frequency, $$$\phi_{C}$$$ is the phase resulting from concomitant gradient fields. The response system for measuring the gradient can be input in any gradient waveform, and a single measurement can be used to predict the current behavior of any acquisition of the eddy current[11]. Using triangular gradient waveforms[5], [6], the B0 eddy current system response ($$$H_{0}$$$) and the gradient field response ($$$H_{1}$$$) were estimated by: $$ H_{c}(\omega)=\frac{\sum_{j} I_{c, j}^{*}(\omega) \cdot O_{c, j}(\omega)}{\sum_{j}\left|I_{c . j}(\omega)\right|^{2}}$$ where $$$ I $$$ is the input waveform, $$$ O $$$ is $$$\phi_{B_{0}}\left(H_{0}\right)$$$ or $$$G^{\text {out }}\left(H_{1}\right)$$$, $$$ j $$$, $$$ c $$$and $$$ \omega $$$ are the measurement waveform index, the gradient channel and the frequency. The B0 eddy current system response measurements and MRF raw data were exported. The B0 eddy current phase and k-space trajectory were calculated by off-line NUFFT reconstruction according to the measured B0 eddy current system response ($$$H_{0}$$$) and gradient field response ($$$H_{1}$$$) : $$ \phi_{B_{0}}(t)=H_{0 x}(t) * G_{x}(t)+H_{0 y}(t) * G_{y}(t)+H_{0 z}(t) * G_{z}(t) $$ $$ \hat{k}_{x, y, z}(t)=H_{x . y . z}(t) * k_{x, y, z}(t) $$ Corrects the Spiral-based MRF with multiplicity , and reconstruct the image through gridding and sampling density compensation[1], [12]. In Vivo Experiment: Head Experiment: All MRI data were acquired on a 5T system (uMR Jupiter, United Imaging, Shanghai, China) and the protocols were approved by the Institutional Reviews Board (IRB). A 48-channel head coil was used on a healthy volunteer, and the whole-brain scanning sequence parameters were set as: TE/TR = 3/15 ms; numbers of TR = 1200; field of view (FOV) = 220×220 $$$\mathrm{mm}^{2}$$$; in-plane resolution = 1.15 × 1.15 $$$\mathrm{mm}^{2}$$$; slice thickness = 5 mm; 5 slices; acquisition time,1 minute and 30 seconds. Abdomen Experiment: Another IRB-approved healthy volunteer underwent an abdominal scan using a 24-channel body array coil and the same 5T magnetic resonance imaging system. MRF scan parameters were: TE/TR = 3/15 ms; numbers of TR = 1200; field of view (FOV) = 300×300 $$$\mathrm{mm}^{2}$$$; in-plane resolution = 1.5 × 1.5 $$$\mathrm{mm}^{2}$$$; slice thickness = 5 mm; 1 slice; acquisition time, 18 seconds.

Results

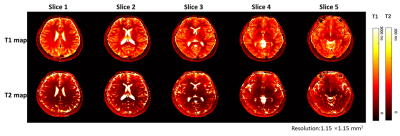
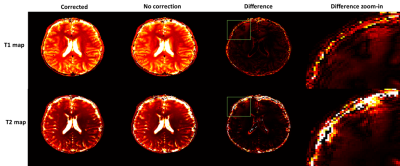
Figure 2 showed five corrected axial slices of a vivo human whole brain at 5T. The proposed method can provide multiple layers of MRF, with no significant results showing that different selection layers have an effect on the corrected images.
Figure 3 demonstrated the comparison of the brain before and after correcting the B0 eddy currents effects. The comparison of difference, especially the comparison of zoom in, shows that the proposed method can alleviate the influence of artifacts caused by B0 eddy currents effects on image quality, but the artifacts existence indicates that there is a gap between artifacts caused by the deviation of actual gradient and predicted gradient.
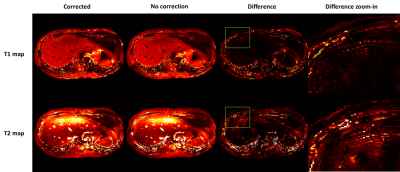
Figure 4 compared to the abdominal MRF before and after correction. The T1 and T2 maps of the liver showed that the artifacts were more severely affected, and our approach was more effective in artifact remission.

Discussion and Conclusion

In this study, the proposed method has been implemented by the gradient impulse response function to correct artifacts caused by B0 eddy currents. All in vivo experiments of head and abdomen at 5T show that the proposed method can effectively reduce MRF artifacts and has potential of whole human body at ultra-high fields.

Acknowledgements

Some of the work was partially supported by the National Natural Science Foundation of China (61871373, 62271474, 81830056, U1805261, 81729003, 81901736, 12026603, 12026603 and 81971611), the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000 and XDC07040000), the High-level Talent Program in Pearl River Talent Plan of Guangdong Province (2019QN01Y986), the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province (2020B1212060051), the Science and Technology Plan Program of Guangzhou (202007030002), the Key Field R&D Program of Guangdong Province (2018B030335001), the Shenzhen Science and Technology Program, Grant Award (JCYJ20210324115810030), and the Shenzhen Science and Technology Program (Grant No. KQTD20180413181834876, and KCXF20211020163408012).