2189
Fast Deep Learning models for Magnetic Resonance Fingerprinting
Raffaella Fiamma Cabini1,2, Davide Cicolari2,3, Leonardo Barzaghi1,4, Paolo Arosio5,6, Stefano Carrazza5,6, Silvia Figini2,7, Marta Filibian2,8, Marco Peviani9, Anna Pichiecchio4,10, and Alessandro Lascialfari2,3
1Mathematics, University of Pavia, Pavia, Italy, 2INFN, Istituto Nazionale di Fisica Nucleare, Pavia, Italy, 3Physics, University of Pavia, Pavia, Italy, 4Advanced Imaging and Radiomics, Department of Neuroradiology, IRCCS Mondino Foundation, Pavia, Italy, 5Physics, University of Milano, Milano, Italy, 6INFN, Istituto Nazionale di Fisica Nucleare, Milano, Italy, 7Department of Social and Political Science, University of Pavia, Pavia, Italy, 8Centro Grandi Strumenti, University of Pavia, Pavia, Italy, 9University of Pavia, Pavia, Italy, 10Department of Brain and Behavioural Sciences, University of Pavia, Pavia, Italy
1Mathematics, University of Pavia, Pavia, Italy, 2INFN, Istituto Nazionale di Fisica Nucleare, Pavia, Italy, 3Physics, University of Pavia, Pavia, Italy, 4Advanced Imaging and Radiomics, Department of Neuroradiology, IRCCS Mondino Foundation, Pavia, Italy, 5Physics, University of Milano, Milano, Italy, 6INFN, Istituto Nazionale di Fisica Nucleare, Milano, Italy, 7Department of Social and Political Science, University of Pavia, Pavia, Italy, 8Centro Grandi Strumenti, University of Pavia, Pavia, Italy, 9University of Pavia, Pavia, Italy, 10Department of Brain and Behavioural Sciences, University of Pavia, Pavia, Italy
Synopsis
Keywords: MR Fingerprinting/Synthetic MR, Data Processing
We proposed a DL method and an automatic hyperparameters optimization strategy to reconstruct T1 and T2 maps acquired with two Magnetic Resonance Fingerprinting (MRF) sequences. The model was trained and validated on a preclinical MRF dataset and tested on an independent test set. Through a lower number of MRF images and a lower k-space sampling percentage than the standard post-processing, the DL-based method and the automatic hyperparameters optimization strategy deliver parametric maps with similar accuracy as the dictionary-based methodology.Introduction
Magnetic Resonance Fingerprinting (MRF) simultaneously measures multiple tissue properties through a more time-efficient acquisition routine than standard mapping techniques1. Because the traditional dictionary-based MRF post-processing framework requires significant computational time and storage capacity, we propose a DL method to reconstruct T1 and T2 maps acquired with two different MRF sequences.Methods
The dataset consists of 6 slices of two ex-vivo brain rat phantoms: 5 slices are from the first phantom and one slice from the second one. We performed the two Gao2 (G-MRF) and Zhao3 (Z-MRF) MRF routines and the reference T1 and T2 mapping sequences (Inversion-Recovery and Spin-Echo) on a 7-Tesla Bruker Scanner. G-MRF and Z-MRF dictionaries were generated by Extended-Phase-Graph formalism4.We defined two different architectures of the DL model: a multilayer perceptron (MLP) and a recurrent neural network (RNN) (Figure1). Both the models are used to perform a voxel-wise regression of the T1 and T2 parameters, given a MRF signal evolution trajectory as input. While MLPs are general purpose models for handling non-specific input data, RNNs are meant to deal with time-series signals to solve temporal problems. The MLP is composed of a sequence of fully connected layers. The input layer consists of a number of nodes equal to the MRF sequence length with a sigmoid activation function, while the output layer consists of 2 nodes for the prediction of T1 and T2 values. The RNN is composed of a long-short term memory (LSTM) block, followed by a fully connected layer with 2 nodes for the output predictions. The set of optimal hyperparameters of the model and the training algorithm were established through an optimization procedure and a k-fold cross validation method (Figure2) cycling on 5 slices of the first phantom. The hyperparameters that were tuned include the architecture of the model (MLP/RNN), model parameters and parameters of the training algorithm.
To train, test and evaluate the generalization ability of the proposed method, we performed a cross validation procedure among different slices of the two phantoms. Particularly, we trained both the models on 5 slices of the first phantom, randomly partitioning the input dataset into two separated subsets (80/20%) for training and validation phases. We used the slice of the second phantom excluded from the training process and from the hyperparameter tuning as an independent test set.
Results
Gold standard T1 and T2 maps, the dictionary-based reconstructed maps and the DL-reconstructed maps are represented in Figure3 for both the G-MRF and Z-MRF datasets. Firstly, we can qualitatively see that the estimated parametric maps of both the methods have correctly reconstructed the anatomical structures of the brain, preserving the visual contrast between different tissues. We can also observe that the range of T1 and T2 maps estimated with all the MRFingerprinting techniques are comparable with the reference T1 and T2 maps. Figure3 shows the error map associated with each parameter computed voxel-wise as the Percentage Relative Error (PRE). The complete list of the PRE mean values and SD are shown in the table of Figure4.We finally analyzed the MRF acquisition in order to determine the acquisition sequence that allows a good estimation of the parametric maps with a shorter acquisition time. We examined the following aspects of the scanning pattern: the length of the MRF acquisition sequence and the sampling percentage of the k-space. Considering the amount of MRF time-points, for G-MRF a good reconstruction of the parametric maps was obtained for a sequence length of at least 60 images for T1 (100 for Z-MRF) and at least 100 images for T2 (100 for Z-MRF), compared to the 300 images necessary for the dictionary-based reconstruction system (400 for Z-MRF). Concerning the k-space sampling percentage, T1 and T2 maps are consistent with a minimum k-space percentage of 30% for both Z-MRF and G-MRF, with respect to the 40% required for the traditional dictionary-based reconstruction method.
Discussion
In this work, we have defined a Deep Learning Neural Network which receives the MRF signal evolution trajectory as input and outputs the estimated values of the two T1 and T2 relaxation maps. The network was trained using experimental MR Fingerprinting data, completely excluding the use of any theoretical MRI signal simulator. To select the best combination of the DL parameters we implemented an automatic hyperparameter optimization strategy. The key aspect of this optimization process is to include all the parameters to the fit, allowing the simultaneous optimization of the NN architecture, the structure of the DL model and the supervised learning algorithm. We compared the reconstruction performances of the DL technique with those achieved from the traditional dictionary-based method. Both the approaches achieved similar performances but the number of MRF time-points and the k-space sampling percentage required were lower for the DL method.Conclusion
Through a lower number of images and a lower k-space sampling percentage than the standard post-processing, DL-based method and automatic hyperparameters optimization strategy deliver parametric maps with similar accuracy as the dictionary-based methodology. Extensions of the proposed methodology to other anatomical regions will be evaluated in the following months.Acknowledgements
No acknowledgement found.References
1Ma et al. "Magnetic resonance fingerprinting." Nature 495.7440 (2013): 187-192.
2Gao et al. "Preclinical MR fingerprinting (MRF) at 7T: effective quantitative imaging for rodent disease models." NMR in Biomedicine 28.3 (2015): 384-394.
3Zhao et al. "Optimal experiment design for magnetic resonance fingerprinting: Cramer-Rao bound meets spin dynamics." IEEE transactions on medical imaging 38.3 (2018): 844-861.
4Weigel. "Extended phase graphs: dephasing, RF pulses, and echoes‐pure and simple." Journal of Magnetic Resonance Imaging 41.2 (2015): 266-295.
Figures
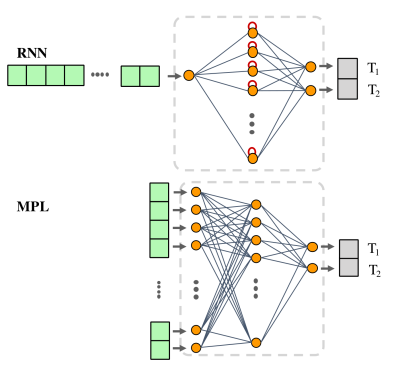
Schematic representation of the two DL models used in the work.
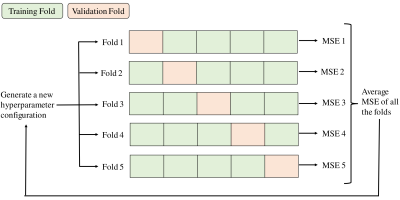
Schematic representation of the k-fold strategy used for the hyperparameter optimization. We performed 1000 iterations of the optimization algorithm and selected the configuration which minimizes the average MSE.
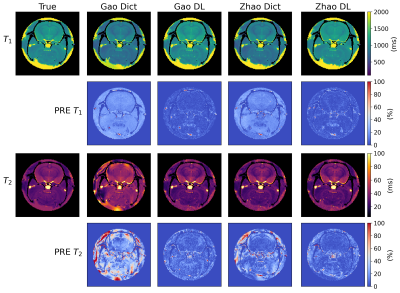
Comparison between the T1 and T2 true maps (first column), those reconstructed with thetraditional dictionary-based method (Dict) and those generated with the Deep Learning (DL) method. Error maps are computed voxel-wise as the percentage relative error (PRE).
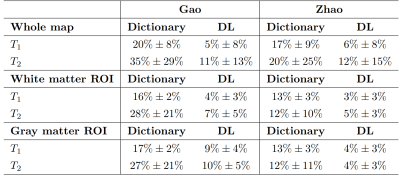
Summary of Percentage Relative Errors of the whole map, White matter Region of Interest (ROI) and Gray Matter ROI.
DOI: https://doi.org/10.58530/2023/2189