Synopsis

Keywords: MR Fingerprinting/Synthetic MR, MR Fingerprinting

Time-resolved magnetic resonance fingerprinting (MRF), or 4D-MRF, has demonstrated its feasibility in motion management in radiotherapy (RT). However, the prohibitive long acquisition time is one of challenges of the clinical implementation of 4D-MRF. The shortening of acquisition time may compromise the accuracies of the predicted tissues’ properties. Here, we propose a novel technique to enhance the accuracies of 4D-MRF with shortened acquisition by optimizing T1 and T2 sensitivities through inter-phase data sharing.

Purpose

Retrospective phase sorting in four-dimensional magnetic resonance fingerprinting (4D-MRF) results in a data truncation and insufficiency issues. The work aims to develop a technique to enhance the precision of multi-phase parametric maps’ accuracies by manipulating the local T1 and T2 sensitivities of each phase.

Methods

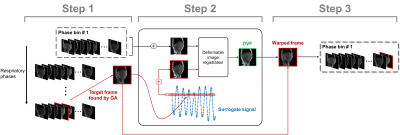
The proposed strategy was enabled by a reconstruction algorithm with a combination of sliding window and compressed sensing reconstruction framework. ^1,2 In brief, sliding window k-space were obtained by the superposition of the spiral interleaves with the window size and sliding distance of 30 and 10, respectively. Retrospective phase sorting was performed on the sliding window domain based on the internal surrogate signal. A Sliding window low-rank compressed sensing (SW-LR-CS) reconstruction was utilized to reconstruct the sliding window frames. An overview of the inter-phase sharing is summarized in Fig. 1. The T1 and T2 sensitivities of signal evolution curves of each phase were quantified by the modified Minkowski distance (MD), which was defined by the sum of the differences between two dictionary elements with a slight variation in T1 or T2.
$$\mathbf{MD}_{T1}\normalsize(T1,T2)=\left[\sum_{t=1}^{{T\scriptsize{p}}'}\mid\mathbf{D}_i(T1+\triangle t_1,T2)-\mathbf{D}_i(T1-\triangle t_1,T2)\mid ^2\right]^{1/2}$$[1]
$$\mathbf{MD}_{T2}\normalsize(T1,T2)=\left[\sum_{t=1}^{{T\scriptsize{p}}'}\mid\mathbf{D}_i(T1,T2+\triangle t_2)-\mathbf{D}_i (T1,T2-\triangle t_2)\mid ^2\right]^{1/2}$$[2]
$$$\triangle t_1$$$ = 50 ms and $$$\triangle t_2$$$ = 5 ms was used in all experiments. An optimization problem was established to maximize the T1 and T2 sensitivities of the dictionary of each phase ($$$\mathbf{D} _p '$$$) by sharing the inter-phase frames with profound sensitivities:
$$argmin _{\mathbf{D}_p'} \sum_{T1,T2} \left[ -\mathbf{W}_1\cdot \mathbf{MD}_{T1}^{\mathbf{MD}_p'}(T1,T2)-\mathbf{W}_2\cdot \mathbf{MD}_{T2}^{\mathbf{MD}_p'}(T1,T2) \right] + W_3\cdot \sum_{t_p=T_p+1} ^{T_p+n_p} \mid A_{t_p}-A_p \mid$$[3]
, where W₁ and W₂ are the weighting matrices. The third term is to ensure the motion consistency by minimizing the absolute differences between the respiratory amplitude of the shared frames ($$$A_{t_p}$$$) and the mean respiratory amplitude of all frames in the target phase p ($$$A_p$$$). Equation [3] was solved by the Genetic algorithm (GA) with integer constrain. ³ Prior to the allocation of the shared frame to the target phase, the deviation in inter-phase motion was compensated using nonrigid image registration. ⁴ To reduce the registration errors, it was performed between the averaged frame of the target phase and a representative frame, which was constructed by combining all frames with the respiratory amplitudes within a defined tolerance level.
Numerical simulations using 4D-extended cardiac-torso (XCAT) digital phantom and in vivo study with volunteer and patient scans on a 3.0 T MRI scanner were performed to validate the proposed approach. An IR-FISP sequence with the following parameters was used in the experiments: spiral out trajectory; variation of flip angle from 0o to 70 o; variation of TR from 11.7 to 14.3 ms; TE = 1.77 ms; total number of frames = 2000; scanning duration = 26 s. The T1 and T2 maps reconstructed by the proposed and conventional methods (filtered back-projection, BP) were quantitatively analyzed by intensity-based metrics, including mean absolute percentage error (MAPE), structural similarity index measure (SSIM), and peak signal-to-noise ratio (PSNR).

Results

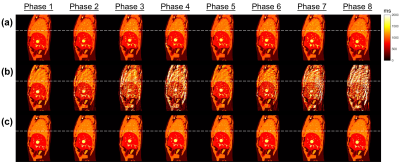
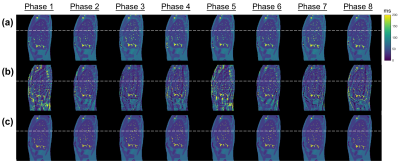
XCAT simulation:
Fig. 2 and 3 show the eight-phases T1 and T2 maps reconstructed by the proposed method and the conventional filtered BP method for the XCAT phantom in the sagittal view with regular breathing pattern. Quantitative results are summarized in Table 1. In brief, the proposed approach achieved the overall MAPE of 7.58% ± 1.46% and 12.5% ± 2.96% (11.90% ± 1.23% and 30.30% ± 6.87%) for the T1 and T2 maps, respectively, in the sagittal view (coronal view) with regular breathing pattern. In contrast, the overall MAPE of T1 and T2 maps generated by the conventional approach were 20.9% ± 10.8% and 28.0% ± 7.96% (35.2% ± 16.9% and 61.8% ± 15.2%), respectively.
In vivo study:
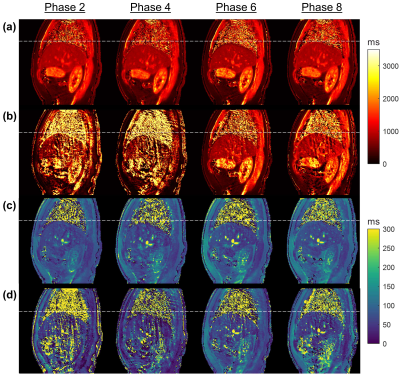
The reconstructed T1 and T2 maps for a representative volunteer using proposed method and filtered BP are presented in Fig. 4. The predicted mean T1 and T2 of liver by the proposed approach were 802ms ± 21.2ms and 66.9ms ± 16.0ms, respectively.

Discussion

Data sufficiency and dictionary sensitivity play an important role in the accuracies of dictionary matching in 4D-MRF, in which data is truncated during phase sorting process. Previous studies suggested that a total number of 500-600 time points yields an optimal balance between parametric maps’ accuracies and scanning efficiency. ^5,6 Data with the temporal length less than 500 is very common in 4D-MRF after the phase sorting. Meanwhile, the frames with potent T1 and T2 sensitivities may be distributed unevenly over different phases after the phase sorting. The interplay of data insufficiency and low sensitivities in 4D-MRF may compromise the accuracies of the reconstructed multi-phase parametric maps. In this work, we have demonstrated a method to tailor the data arrangement of each phase to maximize the dictionary sensitivity to overcome the shortage of time points after phase sorting process.

Conclusion

Manipulation of T1 and T2 sensitivities by inter-phase frame sharing effectively enhanced the precision of multi-phase parametric maps in 4D-MRF.

Acknowledgements

This research was partly supported by research grants of General Research Fund (GRF 15102219), the University Grants Committee, Health and Medical Research Fund (HMRF 06173276), the Food and Health Bureau, Hong Kong Special Administrative Regions.