2176
Multi-parametric quantitative MRI without inversion pulses by optimized RF phase modulation1Division Imaging and Oncology, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
Keywords: MR Fingerprinting/Synthetic MR, Relaxometry
We applied optimized phase modulation to the RF sequence in MR-STAT. We observe that applying optimized phase is beneficial towards the accuracy of T1 and T2 maps, particularly under constrained conditions. In particular, when comparing sequences with and without an initial inversion pulse we observe that the difference vanishes when applying optimized RF phase modulation. Thus optimized phase modulation allows to omit the initial inversion pulse. We hypothesize that the same holds for other multi-parametric qMRI techniques such as MRF.Introduction
Modern multi-parametric quantitative MRI methods include MR-STAT1, MR Fingerprinting (MRF)2, QTI3 and Hybrid-state imaging4. In these methods, flip angle trains are usually time-varying. This gives many degrees of freedom to optimize sequences of flip angles, which is a non-trivial task. Many optimization approaches focus on single-voxel optimization3,5-10, which have been shown to be sub-optimal11 in spatio-temporal techniques such as MR-STAT. Moreover, many optimization approaches are limited to the amplitude of RF pulses3,8-10,12, while it has been shown that appropriate application of phase modulation is beneficial4,13-15. Interestingly, almost all of these methods1-12,14-15 apply an initial inversion pulse – which brings additional power deposition, imperfections of its own and a need for magnetization-relaxation before the pulse17.In this work, we applied the recently proposed analytical framework BLAKJac16 to optimize amplitude and phase of the RF pulses. This is accomplished by acting on the second derivative (or quadratic component) of the phase component (“quadratic phase cycling”). We show that this is particularly beneficial under constrained conditions, such as the absence of an initial inversion pulse, contiguous cyclic application of a sequence17, or when constraining power deposition.
Methods
In our experiments, we used a non-balanced Cartesian MR-STAT sequence on a 3T scanner (Philips Elition), with TR=10ms, TE=5ms, voxel size 1mm x 1mm, slice thickness of 5mm, with a Field Of View of 224mm, requiring 224 phase-encoding steps. The set of phase-encoding steps was repeated 6 times, allowing MR-STAT reconstruction of maps of proton density, T1 and T2. In total, 1344 readout-lines were acquired.RF flip angles were optimized using BLAKJac. BLAKJac is a framework that allows for fast approximation, via the Cramer-Rao Bound, of the noise level in the reconstructed maps, given a flip angle and gradient encoding sequence; this allows for fast optimization of flip-angle trains sequences, while taking into account the gradient encoding strategy. Two scenarios were considered: (A) Amplitude-only: the phase of the pulses was zero; (B) Amplitude+Phase: phase modulation was optimized based on its 2nd time-derivative. This is analogous to applying a (locally) quadratically increasing phase whereby the quadratic component slowly changes over time. See figure 1 for the resulting sequences.
Both scenarios (Amplitude-only) and (Amplitude+Phase) were investigated in four different conditions:
1) initial inversion pulse
2) no initial inversion
3) cyclic repetition of the sequence without pauses nor inversion
4) very stringent SAR limit, with root-mean-squared flip-angle < 10 degrees and no inversion.
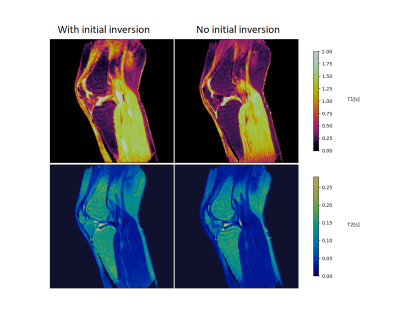
In order to estimate the standard deviations in the resulting maps, each scenario was re-scanned and reconstructed 10 times. The aforementioned set of scans was applied on a Eurospin II phantom set18 (fig. 2) and on the knee of a human volunteer (fig. 3).
Results
In the images (figs. 2 and 3) we observe a substantial difference in noise level between the Amplitude+Phase and the Amplitude-only scenario. This is consistent with the BLAKJac analysis, which predicts that Amplitude+Phase sequences systematically result in lower noise levels than Amplitude-only sequences. For both scenarios, BLAKJac predicts $$$\sigma_4>\sigma_3>\sigma_2>\sigma_1$$$ (where $$$\sigma_i$$$ has to be read as "the noise expected in condition $$$i$$$"). BLAKJac also indicates that the benefit of Amplitude+Phase over Amplitude-only is particularly present for no-inversion, cyclic-repetition, or low SAR conditions (first row of figure 4).The BLAKJac theoretical analysis is confirmed by noise levels measured in a phantom (see second row of fig. 4) and to a lesser degree by the noise levels in-vivo (third row). The figure particularly shows that, when phase is applied, the effect of an inversion pulse is negligible, as shown in fig. 5, thereby suggesting that inversion pulses are not necessary. Contrarily, without phase, those differences are substantial.
Discussion
Each constrained condition has its relevance: reducing the power deposition (condition 4) is of interest for high-field applications. The removal of the (adiabatic) inversion pulse (condition 2) serves the same purpose; moreover, imperfections of this pulse especially at strong B1 inhomogeneities often contribute to quantitative biases. The cyclic repetition condition (3) is of particular interest if repetitive instances of the sequence are to be applied, as e.g. in dynamic imaging or 3D imaging17.Our experiments were conducted with MR-STAT, but the observations likely hold for MRF as well as for other multi-parametric MRI methods.
Conclusion
Applying an optimized RF phase modulation to multi-parametric qMRI sequence is particularly beneficial especially under constrained conditions; examples hereof are sequences without an inversion-prepulse, contiguous cyclic application of the sequence, and sequences exhibiting very stringent SAR restrictions. More importantly, when applying Amplitude+Phase, there is practically no benefit in applying the inversion pulse, which thus can be omitted.Acknowledgements
This work has been financed by NWO grant number 17986References
1. A. Sbrizzi, et al, “Fast quantitative MRI as a nonlinear tomography problem”, Magnetic Resonance Imaging 46(2018): 56-63 O. van der Heide et al, NMR in Biomedicine, 202;33:e4251
2. D. Ma, et al. Magnetic resonance fingerprinting. Nature, 2013;495187–495192.
3. P. Gómez et al. Designing contrasts for rapid, simultaneous parameter quantification and flow visualization with quantitative transient-state imaging. ScientificReports (2019) 9:8468, https://doi.org/10.1038/s41598-019-44832-w
4. J. Assländer et al. Hybrid-state free precession in nuclear magnetic resonance. COMMUNICATIONS PHYSICS (2019) 2:73
5. K. Sommer, et al. Towards predicting the encoding capability of MR fingerprinting sequences. Magnetic Resonance Imaging, Volume 41, September 2017, Pages 7-14.
6. B. Zhao, et al. Optimal Experiment Design for Magnetic Resonance Fingerprinting. Conf Proc IEEE Eng Med Biol Soc. 2016 August ; 2016: 453–456.
7. B. Zhao, et al. Maximum Likelihood Reconstruction for Magnetic Resonance Fingerprinting. IEEE transactions on medical imaging 1812-1823 (2016).
8. O. Cohen, M. Rosen. Algorithm comparison for schedule optimization in MR fingerprinting. Magnetic Resonance Imaging, Volume 41, September 2017, Pages 15-21
9. N. Mickevicius, A. Nencka, E. Paulson. Reducing the Dimensionality of Optimal Experiment Design for Magnetic Resonance Fingerprinting. https://ui.adsabs.harvard.edu/abs/2020arXiv201000674M/abstract
10. P.K. Lee et al. Flexible and efficient optimization of quantitative sequences using automatic differentiation of Bloch simulations. Magn Reson Med. 2019;82:1438–1451
11. M Fuderer, et al. Non-steady-state sequences for multi-parametric MRI need to be evaluated in the context of gradient-encoding, Proc. Intl. Soc. Mag. Reson. Med. (2022), 2786
12. Hu, McGivney, Griswold, Ma. Optimal experimental design of MR Fingerprinting for simultaneous quantification of T1, T2, and ADC. Proc. Intl. Soc. Mag. Reson. Med. (2022), 4802
13. C. Wang, et al. Magnetic resonance fingerprinting with quadratic RF phase for measurement of T2* simultaneously with δf, T1, and T2, Mag. Reson. Med. 2019; 81(3): 1849.
14. X. Wang, D. Hernando, S.B. Reeder. Phase-based T2 mapping with gradient echo imaging. Magnetic resonance in medicine 84.2 (2020): 609-619.
15. H. Liu, et al. Increasing the T2 sensitivity of MR-STAT sequences by small quadratic RF phase increments, Proc. Intl. Soc. Mag. Reson. Med. (2022), 0625
16. M. Fuderer, et al. Efficient performance analysis and optimization of transient-state sequences for multi-parametric MRI, NMR in Biomedicine (2022, in press).
17. T. Amthor et al. Magnetic Resonance Fingerprinting with short relaxation intervals.
18. TO5, Eurospin II test system, Scotland
Figures

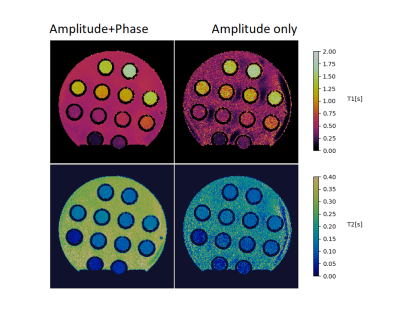
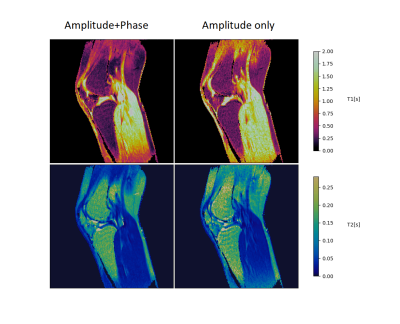
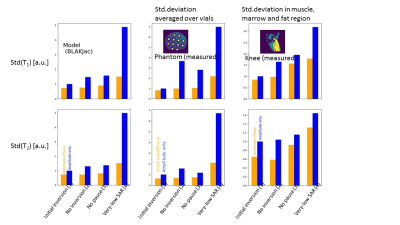
Fig. 4: Predicted (1st column) and measured (2nd and 3rd columns) noise levels.. (All the noise values have been scaled relative to the Amplitude-only scenario of the Initial-inversion condition.)
It is clear that Amplitude+Phase is always beneficial over Amplitude-only; these differences are in general larger at conditions 2, 3 and 4. The orange bars are very similar between condition 1 and 2, suggesting that an initial-inversion pulse is not needed if an optimized Amplitude+Phase scenario is applied.