Synopsis

Keywords: Image Reconstruction, Signal Representations

A model-based image reconstruction (MBIR) framework is developed for highly accelerated point spread function (PSF) encoded echo planar imaging (EPI). The reconstruction accounts for known physics, and utilizes a subspace representation with local low-rank (LLR) regularization along with a variable splitting solution. Comparisons with images obtained through standard methods demonstrate considerable artifact reduction and sharpness preservation through MBIR. MBIR accommodates arbitrary sampling trajectories along the PSF-encoding dimension, enabling reconstruction of quality images from less than one minute of scan time; and we demonstrate performance boosts with nonstandard trajectories precluded by conventional reconstruction methods.

Introduction

Echo planar imaging (EPI)¹ comprises fast acquisition facilitating advanced MR applications. Low effective phase encoding bandwidth and system non-idealities limit single-shot EPI practically to relatively low-resolution exams. Point spread function (PSF)-encoded EPI^2-4 utilizes multi-shot auxiliary phase encoding, enabling projection into undistorted images following reconstruction (through standard methods) of an interim PSF volume. Despite in-plane and reduced field of view (rFOV) acceleration, the number of shots required for PSF-EPI remains relatively high with classical methods; scan time remains a limitation. While shots are considerably reducible with tilted CAIPI⁵, this requires PSF-encoded calibration. Extending to time-resolved acquisition with subspace reconstruction⁶ enables multi-contrast imaging, but in current form, requires algorithmic $$$B_0$$$ updates.
This work extends prior preliminary efforts⁷ to investigate model-based image reconstruction (MBIR)⁸ for highly accelerated PSF-EPI, combining known physics, partial temporal separability, and regularization to directly estimate undistorted images with arbitrary sampling of the PSF space.

Theory

A scalar forward-mapped signal model for PSF-EPI is
$$\mathbf{G}[u,p,v,c]\approx\sum_i\sum_l\mathbf{S}[i,l,c]\mathbf{f}[i,l]e^{-\mathbf{z}[i,l]\tau[v]}e^{-\jmath \mathbf{k}_x[u]\mathbf{x}[i]}e^{-\jmath \mathbf{k}_y[v]\mathbf{y}[l]}e^{-\jmath \mathbf{k}_a[p]\mathbf{y}[l]}+\mathbf{\epsilon}[ u,p,v,c ]$$
where $$$u,p,v,$$$ and $$$c$$$ respectively index measurements at readout, pass (for auxiliary PSF encoding), phase-encoding, and coils; $$$\mathbf{S}$$$ are coil sensitivity profiles; $$$\mathbf{f}$$$ and $$$\mathbf{z}$$$ are unknown magnetization and rate map⁸ arrays of interest, the latter encompassing relaxation and off-resonance effects; $$$\tau[v]$$$ denotes post-RF acquisition time for $$$v$$$th phase encodings; $$$\mathbf{k}_x, \mathbf{k}_y,$$$ and $$$\mathbf{k}_a$$$ respectively are $$$k$$$-space encoding along readout, phase, and auxiliary (PSF); $$$\mathbf{x}[i], \mathbf{y}[l]$$$ are spatial coordinates and associated indices; and $$$\mathbf{\epsilon}$$$ is a zero-mean complex Gaussian noise instance. An abstracted signal model written as the 3rd tensor unfolding⁹ of $$$\mathbf{G}$$$ is
$$\mathbf{G}_{[3]}=\sum_{v,c}\big(\delta_c\otimes\mathbf{\Lambda}_v\text{diag}(\mathbf{S}_{[3]}\delta_c)\big)\mathbf{M}\mathbf{X}\mathbf{\psi}_K^*\delta_v\delta_v^T+\mathbf{\epsilon}_{[3]}$$
where $$$\delta$$$ is Kronecker's delta, and the transform operator is
$$\mathbf{\Lambda}_v\overset{\Delta}{=}\big(\mathbf{\Xi}_\text{psf}\mathbf{F}_\text{psf}\otimes\mathbf{I}_{N_x}\big)\big(\text{diag}((\mathbf{\Xi}_\text{pe}\mathbf{F}_\text{pe})^T\delta_v)\otimes\mathbf{I}_{N_x}\big)\big(\mathbf{I}_{N_y}\otimes\mathbf{F}_\text{ro}\big),$$
where $$$\mathbf{F}_\text{ro},\mathbf{F}_\text{pe}$$$ and $$$\mathbf{F}_\text{psf}$$$ are respectively Fourier transforms along readout, phase-encoding, and PSF encoding, with associated subsampling operators $$$\mathbf{\Xi}$$$. $$$\mathbf{I}_{N}$$$ is an identity matrix of size $$$N$$$. $$$N_x$$$ and $$$N_y$$$ are image dimensions; $$$N_{v}, N_{c}$$$, and $$$N_{p}$$$, the number of phase encodings, channels, and PSF encodings.
This signal model has embedded representations to reduce the search space and/or exploit low-rank characteristics in reconstruction. First, $$$\mathbf{M}$$$ is an undersampled identity matrix confining unknown voxels to known spatial support¹⁰. Next, partial temporal separability¹¹ is directly embedded: we target a composite unknown $$$\mathbf{\theta}\in\mathbb{C}^{N_i \times N_v}$$$ comprising both magnetization and rate map effects evolving temporally through phase-encodings, confined to known support where $$$N_i$$$ is the number of voxels of interest. We approximate this unknown with $$$\mathbf{\theta}=\mathbf{\theta}\mathbf{\psi}\mathbf{\psi}^*\approx\mathbf{\theta}\mathbf{\psi}_K\mathbf{\psi_K^*}\equiv\mathbf{X}\mathbf{\psi}_K^*$$$, where $$$\mathbf{\psi}$$$ is an orthonormal temporal basis and $$$\mathbf{\psi}_K=\text{span}\begin{bmatrix}\mathbf{\phi}_1&\dots&\mathbf{\phi}_K\end{bmatrix}$$$¹². The reconstruction target is the set $$$\mathbf{X}\in\mathbb{C}^{N_i \times K}$$$ of basis expansion coefficients, and $$$\mathbf{\psi}_K\in\mathbb{C}^{N_v \times K},K<N_v$$$, is a matrix of precomputed temporal basis vectors^6,12.
To facilitate subsampling operator decoupling in a variable splitting solution^13,14, we rewrite $$$\mathbf{\Lambda}_v$$$ in an alternate form and approach the objective
$$\mathcal{J}(\mathbf{X})\overset{\Delta}{=}\big\Vert\sum_{c,v}(\mathbf{I}_{N_c}\otimes\mathbf{H})(\delta_c\otimes\mathbf{K}_v\text{diag}(\mathbf{S}_{[3]} \delta_c))\mathbf{M}\mathbf{X}\mathbf{\psi}_K^*\delta_v\delta_v^T-\mathbf{G}_{[3]} \big\Vert_F^2+\alpha\sum_{r\in\zeta}\big\Vert\mathbf{E}_r\mathbf{M}[\mathbf{X}\ |\ \overline{\mathbf{X}}]\big\Vert_*$$
where $$$\Vert\cdot\Vert_F$$$ and $$$\Vert\cdot\Vert_*$$$ are Frobenius and nuclear norms. We promote local low-rank (LLR)^15,16 on weighting coefficients describing temporal evolution of images¹², appended across columns with conjugates to encourage smooth phase¹⁷. $$$\mathbf{E}_r$$$ is an extraction operator for block $$$r$$$ from the set $$$\zeta$$$ for LLR promotion; $$$\alpha$$$ is a regularization parameter. We solve this with alternating direction method of multipliers (ADMM)¹⁸, applying variable splitting described in Figure 2.

Methods

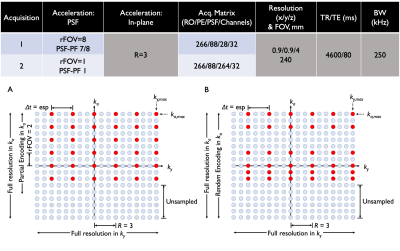
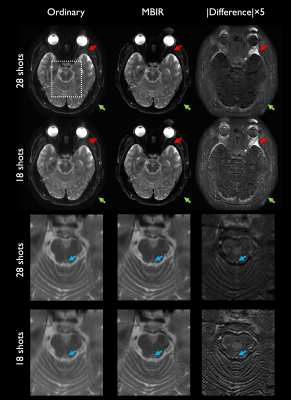
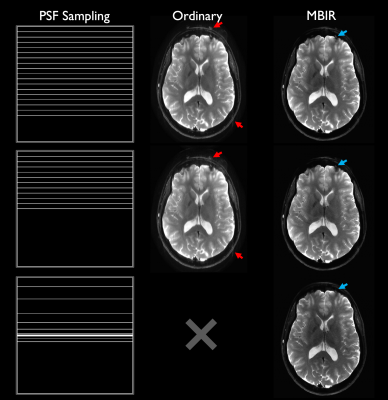
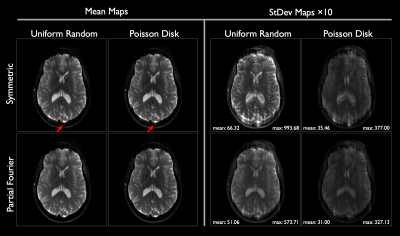
Following an IRB-approved protocol, volunteers were scanned on a compact 3T scanner¹⁹ with accelerated T2-weighted PSF-EPI (T2-DIADEM)²⁰ with parameters in Figure 1. Partial Fourier acceleration was applied only along PSF. Coil sensitivities were generated with ESPIRiT²¹. In a conventional reconstruction, PSF volumes were reconstructed by unfolding in-plane images with SENSE²². Partial Fourier PSF reconstruction comprised zero-filling with rFOV unfolding⁴. Conversely, MBIR was run. Temporal basis vectors were precomputed following simulations^6,12 using field map data from a prior study²³; we set $$$K=31$$$. PSF-EPI data were retrospectively truncated from 28 (7/8 PSF-PF, 2:09 m:s actual scan time) to 18 shots (9/16 PSF-PF, 1:23 m:s simulated) and reconstructed for comparison. Additionally, in vivo brain data were acquired with full PSF-encoding, then retrospectively undersampled uniformly $$$12\times$$$ along PSF, then reconstructed. Further, data were undersampled with 50 distinct 12-shot random sampling instances (55.2 s simulated scan time) in uniform-random and 1D Poisson-disk patterns, with and without partial Fourier along PSF, and reconstructed with MBIR. Figure 1 depicts sampling variants.

Reconstruction was completed using Matlab. $$$k$$$-space preprocessing comprised ramp sampling and Nyquist ghost correction using vendor-provided tools. Image post-processing steps included zero-padding, Fermi filtering, scaling, and vendor-provided gradient nonlinearity correction.

Results

Figure 3 illustrates reconstruction comparisons between full-duration and truncated data with prospective acceleration. Figure 4 demonstrates performance with subsampling to <1 minute of scan time. In both cases, for each sampling instance, MBIR exhibits fewer residual artifacts than standard. Sharpness is preserved despite aggressive partial PSF encoding. Random encoding suppresses artifacts furthermore. Figure 5 shows MBIR performance with distinct random sampling patterns, demonstrating best results with 1D Poisson disk and partial encoding.

Discussion and Conclusion

Our MBIR framework for PSF-EPI directly reconstructs high-quality undistorted images. Reconstructions are superior relative to standard methods with uniform acceleration, exhibiting fewer artifacts and improved detectability. MBIR accommodates arbitrary PSF sampling, unachievable by classical reconstructions, producing quality images from <1 minute of scan data$$$-$$$with nonstandard sampling achieving best performance. MBIR thus extends PSF-EPI beyond previously possible capabilities. Ongoing work includes a radiologists' evaluation.

Acknowledgements

This work is supported by NIH U01 EB024450, the National Science Foundation Graduate Research Fellowship Program, and Mayo Clinic Graduate School of Biomedical Sciences.