Synopsis

Keywords: Image Reconstruction, Parallel Imaging

The background phase variations exist in coil sensitivities. Optimized phase distribution can minimize the noise of the parallel MRI reconstruction. However, phase variation may be originated from different factors, and it is difficult to be modeled. A random feature method is proposed to model phase variations in coil sensitivities. Through a linear reconstruction using the random phase feature, background noise can be suppressed. Augmented phase features make the linear reconstruction better remove background noise.

Introduction

In parallel magnetic resonance imaging (pMRI), background phase variation exists in coil sensitivities ¹, where there are fixed background phase distributions, yielding a minimized noise enhancement. But these optimized phase distributions are not easy to be calculated and have not been applied in actual experiments ¹. The optimized background phase distributions depend on coil arrangement, acceleration factor, and object shape. We intend to find the optimized background phase distribution for minimizing the noise of the pMRI reconstruction.

Methods

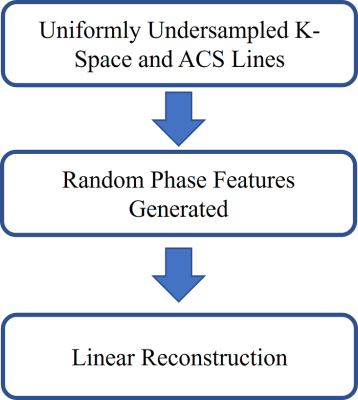
In parallel MRI, one coil’s k-space data denote the Fourier Transform of the distribution of the spatial spins combined with the coil sensitivities. Furthermore, in practical imaging, background phase effects caused by B0 field inhomogeneity, flow, and pulse sequence also exist in the effective coil sensitivities. The coil k-space data can be represented as ¹: $$$ S_j (p) = FT \Bigl( \rho(x)\cdot e^{i\varphi(x)} \cdot C_j (x) \Bigl) $$$ (1), where $$$ρ(x)$$$ represents the spin distribution, $$$ e^{i\varphi(x)} $$$ denotes background phase, $$$ C_j (x) $$$ is the coil sensitivities of the jth coil, $$$p$$$ is the k-space data vector, and $$$x$$$ represents the vector in the image domain. The symmetric complex-conjugate k-space data can be represented as ¹: $$$ S_j^* (p)=FT \Bigr[ ρ(x) \cdot e^{-i\varphi(x)} \cdot C_j^* (x) \Bigr] $$$ (2), where $$$*$$$ is the complex-conjugate operator. Additional phase information is provided in the virtual conjugate coil (VCC), although the magnitude sensitivities are the same between actual and virtual coils.

The phase variations may arise from the transmit RF phase, gradient non-linearities, susceptibility variations, special techniques such as flow encoding, or various other sequence-dependent factors ². Since the phase variations depend on a variety of factors, they could be considered as random variables. It may be difficult to accurately estimate the phase variations. For this reason, adding random phase features to each coil k-space signals may augment the training data for enhancing the training performance and therefore enhancing the reconstruction performance. Random features can be categorized as the data-dependent and data-independent groups ³. A reproducing kernel Hilbert space (RKHS) induced by a random feature can be dense in the space of continuous functions under the supremum norm ⁴. A new random phase feature is proposed and random phases have the uniform distribution on [0,2π]. The kernel mapping $$$ϕ$$$ is defined as $$$ ϕ(p)=\Bigr[ |p| e^{-iθ_1} , e^{-iθ_2} ,⋯,e^{-iθ_m} \Bigr] $$$ (3), where $$$|p|$$$ represents the magnitude of k-space signal, and $$$θ$$$ denotes the phase angle. The phase angle is randomly generated by: $$$θ=random(p)$$$ (4), and uniformly distributed on $$$[0,2π]$$$. The flowchart is presented in Figure 1. We use the linear reconstruction GRAPPA ⁵, as a routine clinical method, for evaluating the performance of suppressing the noise, because the linear reconstruction is transparent compared to the black-box property of machine learning/deep learning based nonlinear reconstruction. So, the effects of random phase features may be easier to be observed and analyzed.

Results

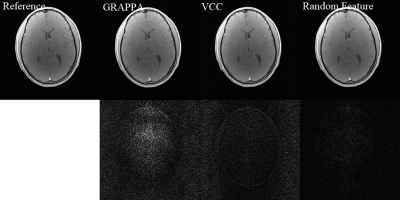
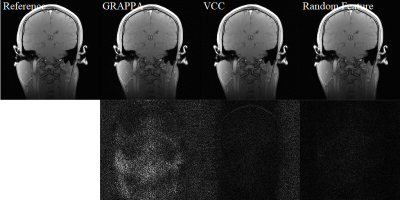
Two datasets are used to evaluate the reconstruction performance. The first dataset of axial brain images was acquired on a 3T scanner with a 32-channel head coil using a 2D gradient echo sequence (TE/TR = 2.29/100 ms, flip angle = 25°, matrix size = 256 × 256, slice thickness = 3 mm, and FOV = 24 × 24 cm²). The second set of coronary brain data was acquired using a 2D gradient echo sequence (slice thickness = 3.0 mm, matrix size = 256 × 256, FOV = 24 × 24 cm², and TE/TR = 2.29/100 ms). ACS lines are 20 or 30, and the outer reduction factor is 4. All images were reconstructed on a computer with an i7 CPU and 32GB RAM.
For brain images content as shown in Figures 2 and 3, the proposed random phase feature method has similar SNR in comparison to the VCC method ⁸. Difference maps are extracted from the subtraction between the reconstructed images and the reference image with fully sampled data. Based on the amplified difference maps, the proposed method can suppress more noise in the backgrounds. On the other hand, GRAPPA and VCC method has low SNR in the backgrounds. Quantitative evaluation results are illustrated in the Figure 4. It is seen that the proposed method has better NMSE, PSNR, and SSIM metric values than those of other two methods.

Discussion

Only linear reconstruction is evaluated because linear reconstruction is easier to be interpreted and more transparent than nonlinear reconstruction. Although VCC can also improve kernel learning-based ⁶ and deep learning-based ⁷ reconstructions, due to the black-box property in nonlinear learning procedures, it is not clear whether the proposed random phase modeling can enhance SNR in an interpretable way.

Conclusion

Background SNR of the linear reconstruction GRAPPA is improved by modeling the phase distribution with random phase features. The random phase feature will be studied for learning-based nonlinear reconstruction in the future.

Acknowledgements

No acknowledgement found.