Synopsis

Keywords: Motion Correction, Head & Neck/ENT

SAMER uses a fast reference scan (“scout”) and short additional guidance lines in each shot of an MPRAGE sequence (“linear⁺ reordering”) to calculate motion parameters. Optimization of rigid body motion parameters are typically nonlinear. In this work we exploit local linearity with SAMER to improve the performance. During motion estimation, the initial guess of motion parameters for a given shot is taken from the previous most similar shot. Similarity is determined by correlations of the linear⁺ guidance lines. Retrospective reconstructions of volunteer data show the proposed method has very good computation performance and can handle large motion well.

Introduction

Retrospective motion-correction methods attempt to reconstruct artifact-free images from corrupted measurement data. One class of algorithms is model-based¹ where normally image and motion parameters are solved for iteratively by alternating between two separate steps. To decouple image reconstruction from motion estimation, SAMER uses a scout and short additional guidance lines (“linear⁺ reordering”)² to calculate rigid motion parameters for every shot by non-linear optimization. It can be performed during scanning after data is acquired for a shot. With all shots’ motion parameters, the final image is reconstructed. Here linear motion optimization³ is proposed with optional external signal such as Pilot Tone. It is demonstrated that linear motion optimization has a much-improved computation performance in all-shots optimization scenario. However, without the scout, the two-step optimization is still required, thus a per-shot motion optimization is not possible. We would like to further improve performance by using linear motion optimization with SAMER method.

Methods

Here, we propose a linear motion optimization method with scout and linear⁺ guidance lines. We first give a brief description of the symbols involved:
$$$\hat{x}$$$: scout image.
$$$y$$$: SAMER linear⁺ guidance lines k-space data.
$$$T$$$: rigid motion transformation matrix.
$$$a$$$: rigid motion parameters vector (size of 6*1) for a shot, $$$\hat{a}$$$ is current estimation of $$$a$$$.
$$$A$$$: sampling mask matrix for SAMER guidance lines.
$$$F$$$: FFT operator.
$$$S$$$: coil sensitivity maps.
$$$G$$$: negative gradient of the motion transformed image, with current $$$\hat{x}$$$ and $$$\hat{a},G=-\triangledown(T(\hat{a})\hat{x})$$$
$$$D$$$: a set of predefined displacement basis matrices for 3D rigid motion, which contains the basis matrices of 3 rotations and 3 translations. Any 3D rigid displacement field $$$u$$$ with small rotations can be linear combination of $$$D, u = Da$$$.
$$$r$$$: current residual of guidance lines k-space data, $$$r=y–AFST(\hat{a})\hat{x}$$$

By linear motion optimization², we have:
$$AFSGD\triangle a=r\tag{1}$$
With (1), we have following algorithm:
Algorithm
For each shot
$$$\hspace{2em}$$$Initialize motion parameters $$$\hat{x_1}$$$
$$$\hspace{2em}$$$For iteration i = 1 to max_iterations
$$$\hspace{4em}$$$ $$$r = y – AFST(\hat{a_i})\hat{x}$$$, if $$$\lVert r \rVert/\lVert y \rVert$$$ start to increase or reach maximum iterations, break.
$$$\hspace{4em}$$$ $$$G=-\triangledown(T(\hat{a_i})\hat{x})$$$
$$$\hspace{4em}$$$ Explicitly construct matrix $$$R = AFSGD\triangle a$$$ ($$$AF$$$ is a DFT matrix)
$$$\hspace{4em}$$$ Get $$$\triangle \hat{a}$$$ by solving linear equation: $$$R\triangle a = r $$$
$$$\hspace{4em}$$$ $$$\hat{a_{i+1}} = \hat{a_i} + \triangle \hat{a}$$$
$$$\hspace{2em}$$$end
end
Initial values of $$$\hat{a}$$$
For first shot, initial values of $$$\hat{a}$$$ are 0.
For the i^th shot (i > 2), initialize shot i with the previously calculated values where the guidance lines show the highest correlation. If not indicated otherwise, we use this method for linear SAMER.
There are other methods to set initial values of $$$\hat{a}$$$: starting with 0 or starting from last shot’s values.
Tests
Volunteer tests were performed on a 3T MRI system (MAGNETOM Vida, Siemens Healthcare, Erlangen, Germany), using a 20-channel head coil. Volunteers were asked to perform the following head motions: 1) keep still, 2) move with breathing, 3) move in steps, and 4) move freely. A 3D MPRAGE (TR=2.3sec) prototype sequence with scout and linear⁺ reordering was used for scanning. The data matrix size is 256 * 256 * 224 with resolution of 0.9375mm* 0.9375mm*0.9mm. Data were reconstructed retrospectively. The processing was performed with a C++ implementation on Intel i7-9750H CPU. We compared the quality of the motion corrected images and motion estimation time of the original SAMER approach and linear SAMER.

Results and Discussion

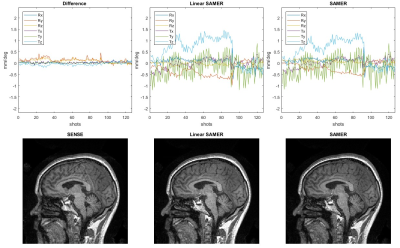
Generally, both linear SAMER and original SAMER significantly reduce motion artifacts.
Figure 1 shows an unconscious motion case where the volunteer was asked to keep still. Both linear SAMER and SAMER work very well in reducing motion artifacts.
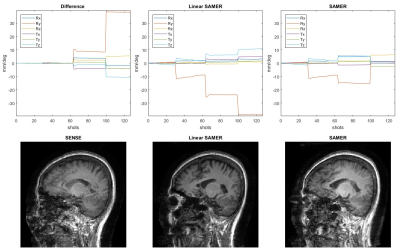
Figure 2 shows a large motion case where the volunteer was asked to rotate his head by steps. Linear SAMER shows better reduction of motion artifacts than SAMER.
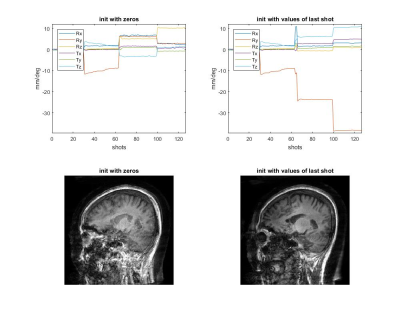
Figure 3 shows linear SAMER results with the two initialization methods mentioned above: initialization with 0 and initialization with the values from the last shot. Both methods fail to get the optimal motion values and get stuck in local minimal. This indicates that a better initial guess can improve the results significantly.
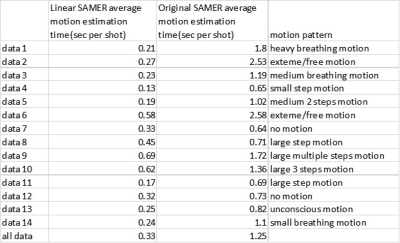
The optimization time for motion detection is displayed in Figure 4. The average for linear SAMER motion estimation time per-shot is about 0.33s. Linear SAMER improves the motion estimation time by about 275% compared to the original SAMER approach. Tests were performed on a laptop computer. Clinical image reconstruction computers are normally more powerful; thus, we expect the motion optimization time on such a system to be faster.

Conclusion

Our results demonstrate that the proposed method can perform fast motion estimation to obtain motion parameters in under a second after the data acquisition of each shot, thus the final image reconstruction can be performed almost immediately. The correlation-based initialization of the proposed method was shown to be able to cope even with large motion cases.

Acknowledgements

No acknowledgement found.