1889
BayesNetCNN: incorporating uncertainty in neural networks for image-based classification tasks
Matteo Ferrante1, Tommaso Boccato2, Marianna Inglese2, and Nicola Toschi3,4
1Biomedicine and prevention, University of Rome Tor Vergata, Roma, Italy, 2Biomedicine and prevention, University of Rome Tor Vergata, Rome, Italy, 3BioMedicine and prevention, University of Rome Tor Vergata, Rome, Italy, 4Department of Radiology,, Athinoula A. Martinos Center for Biomedical Imaging and Harvard Medical school, Boston, MA, USA, Boston, MA, United States
1Biomedicine and prevention, University of Rome Tor Vergata, Roma, Italy, 2Biomedicine and prevention, University of Rome Tor Vergata, Rome, Italy, 3BioMedicine and prevention, University of Rome Tor Vergata, Rome, Italy, 4Department of Radiology,, Athinoula A. Martinos Center for Biomedical Imaging and Harvard Medical school, Boston, MA, USA, Boston, MA, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Alzheimer's Disease
The willingness to trust predictions formulated by automatic algorithms is key in a vast number of domains. We propose converting a standard neural network into a Bayesian neural network and estimating the variability of predictions by sampling different networks at inference time. We use a rejection-based approach to increase classification accuracy from 0.86 to 0.95 while retaining 75% of the test set for Alzheimer disease classification from MRI morphometry images. Estimating uncertainty of a prediction and modulating the behavior of the network to a desirable degree of confidence, represents a crucial step in the direction of responsible and trustworthy AI.Introduction
The willingness to trust predictions formulated by automatic algorithms is key in a vast number of domains. Whilst extremely powerful, a vast number of deep architectures are only able to formulate predictions without an associated uncertainty, critically reducing user compliance even when explainability techniques are used. This issue is particularly sensitive when deep learning techniques are employed e.g. in the medical diagnosis field. In this context, Alzheimer's disease (AD) is one of the most critical public health concerns of our time. AD diagnosis is still based on clinical presentation and confirmed using magnetic resonance imaging (MRI)(Spasov et al., 2019) or positron emission tomography (PET), generating a great deal of subjectivity and uncertainty when positioning a patient within the AD continuum. There is great interest in models able to detect and predict AD-related structural and functional changes, however difficulties in accessing large-scale curated datasets and the need to work with multimodal high-dimensional data call for particular attention in avoiding overfitting and increasing the reliability of automatic models, possibly including the output of uncertainty estimates which can be evaluated by neuroscientists and physicians. Here we propose a Hybrid Bayesian Neural Network (MacKay, 1995) where predicted probabilities are coupled with their uncertainties and a tunable rejection-based approach, allowing the user to select a desirable degree of confidence.Data
We selected a subset (376 images, 50% AD, 50% healthy, 80(train)/20(test) split) of the ADNI dataset, composed of cases labeled as both healthy subjects and AD and employed the T1-weighted image only. All images were nonlinearly coregistered to the MNI T1 template, after which subject-wise Jacobian Determinant maps in MNI space were computed (JD) for each subjects, representing local degree of atrophy. JD images were used as input for our architecture.Methods
Instead of estimating $$$w$$$ ,where $$$w$$$ is the set of network weights that minimizes the cost function, we learn a weight distribution (equivalent to an infinite ensemble approach, which allows us to estimate the variance of the prediction). We, therefore, learn the posterior, where represents the input data, and perform inference as the average of different neural networks as $$p(\hat{y}|D)=\int_w p(y|w)p(w|D)dw = E_{p(w|D)}(p(y|w))$$ Instead of attempting to estimate p(w|D) by approximating it with a parametrized $$$q_{\phi}(z)$$$ distribution that minimizes the KL divergence with the target distribution, in this paper, we implement a hybrid approach which entails first training a standard convolutional network and then turning the weights of the last layer into a narrow Gaussian distributions centered on the optimal weight values $$ p(w|D)= \frac{p(D|w)p(w)}{\int_{w'} p(D|w')p(w')dw'}$$Our base model is a residual convolutional neural network based on depthwise separable convolutions, which reduce the number of parameters from $$$COK^3$$$ to $$$C(K^3+O)$$$ with K as kernel dimension, C number in input channels and O number of output channels. Each block is composed of two depthwise separable convolutions with a PReLU activation function. A flattening layer is followed by a linear layer for the first part of the training and then turned into a Bayesian linear layer replacing optimal values with Gaussian distributions. After training, the last layer’s weights are replaced by a set of Gaussians $$$w^* \rightarrow N(w^*,s)$$$ (s=0.001 in this paper), and a set of weights is sampled from this distribution. Sampling networks at inference time produces a set of predictions and allows us to estimate uncertainty about the output. Also, integrating gradients allowed us to produce saliency maps which depict the brain regions which contribute most to the prediction.
Results
Using the “standard” neural network obtained a classification accuracy (AD vs healthy controls) of 0.86. Successively, our approach was tested as a function of t (i.e. the maximum standard deviation accepted for the class with the highest probability). As the threshold is reduced, the accuracy and AUC increase while the fraction of the remaining test dataset decreases since the model is rejecting the predictions whose associated uncertainty exceeds the threshold. We observed the best results with a threshold of 0.002, which corresponds to retaining 75% of the dataset and reaches an accuracy of 0.95 and AUC of 0.96.Discussion
Ethics and responsibility pose an upper bound on the contribution of artificial intelligence in medical diagnosis, screening, and triaging. Being able to estimate the uncertainty of a prediction, along with modulating the behavior of the network to a degree of confidence that the user is informed about can represent a crucial step in this direction. Such features can improve the translation from research to clinical predictive models. Rather than completely replacing humans in evaluation, AI can support extremely useful recommendation systems and powerful tools to reduce workload in an efficient way for e.g. medical professionals. Here proposed a method that turns a classical neural network into a Bayesian neural network, hence endowing the model with the ability to estimate the uncertainty associated with predictions. We also incorporate a rejection method based on a threshold based on thresholding the estimated uncertainty, which has resulted in a global performance increase that, to our knowledge, is beyond state-of-the-art in AD discrimination when using T1-w images only.Acknowledgements
Part of this work is supported by the EXPERIENCE project (European Union’s Horizon 2020 research and innovation program under grant agreement No. 101017727)Matteo Ferrante is a Ph.D. student enrolled in the National PhD in Artificial Intelligence, XXXVII cycle, course on Health and life sciences, organized by Università Campus Bio-Medico di Roma.References
MacKay, D. J. C. (1995). Bayesian neural networks and density networks. Nuclear Inst. and Methods in Physics Research, A, 354(1), 73–80. https://doi.org/10.1016/0168-9002(94)00931-7 Spasov, S., Passamonti, L., Duggento, A., Liò, P., & Toschi, N. (2019). A parameter-efficient deep learning approach to predict conversion from mild cognitive impairment to Alzheimer’s disease. NeuroImage, 189(January), 276–287. https://doi.org/10.1016/j.neuroimage.2019.01.031Figures
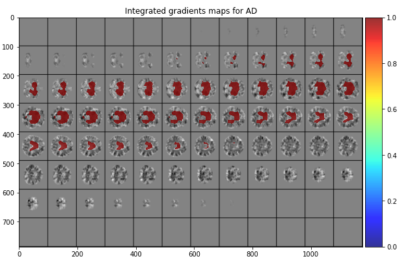
Integrated Gradients which show where the model
is focusing, confirming the importance of e.g. ventricular and temporal
hypertrophy in radiologically detecting AD
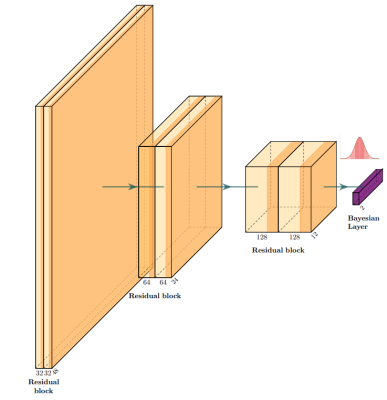
Visual
representation of the architecture. At each inference, weights are sampled from the gaussian distribution for the bayesian layer to get a specific network.
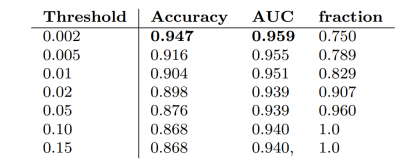
Table with Accuracy, AUC and fraction of test set with standard deviation below
the threshold in functions of the threshold chosen
DOI: https://doi.org/10.58530/2023/1889