1823
Velocity-Encoding Navigator for First-Order Motion Compensation in Diffusion MRI
Bo Li1 and Thomas Ernst1
1Department of Diagnostic Radiology and Nuclear Medicine, University of Maryland, Baltimore, Baltimore, MD, United States
1Department of Diagnostic Radiology and Nuclear Medicine, University of Maryland, Baltimore, Baltimore, MD, United States
Synopsis
Keywords: Motion Correction, Diffusion/other diffusion imaging techniques, velocity navigator
Uncorrected head rotations during diffusion weighted imaging (DWI) can induce gradient imbalances that may shift the echo outside of the k-space window and cause signal dropouts. Therefore, we developed a rotational velocity navigator (~10ms duration) that is acquired immediately after each excitation and estimates the rotational velocities perpendicular to the diffusion gradient. The accuracy of estimated velocities was 4.1°/s relative to an optical tracking system (“gold standard”). Ultimately, the rotational velocities can predict the gradient moment error in first order, and a gradient blip can be applied to recenter the echo in k-space.Introduction
Diffusion weighted imaging (DWI) typically uses spin-echo sequences with diffusion sensitizing gradients. However, the large amplitude and long duration of the diffusion gradients make these sequences sensitive to movements. “Intra-scan” rotations between excitation and readout can disturb the gradient balance of a DWI sequence, and can push the signal (echo) outside of the sampled k-space [1]. The resulting signal losses or dropouts can be reduced using several acquisition-based approaches: a. Motion compensation methods modify diffusion gradient waveforms to eliminate 1st or 2nd-order motion effects on gradient balance [1-5]. They are appealing due to relative ease of implementation but suffer from marked increases in TE [4] (~25-30ms for b ≥ 1,000mm/s2) and unacceptable SNR decreases (~30%). b. Another method detects diffusion weightings with a high likelihood of motion in real-time and reacquires flagged scans [6]. However, this requires arbitrary thresholds and does not address smaller errors in signals. c. Finally, we and other groups have demonstrated the utility of prospective motion correction (PMC) with optical tracking [7-10]. These fast techniques can rebalance gradient moments between excitation and refocusing, but optical tracking systems still have limited availability. Therefore, we developed a new “rotational velocity navigator”. This vrotNav is acquired immediately after excitation and provides estimates of rotational velocities perpendicular to the diffusion gradient. The ultimate goal is to use the estimated rotational velocities to calculate the current gradient imbalance and apply a gradient blip in the second TE/2 period to minimize gradient imbalances, similar to the approach in reference [9].Theory
The gradient moment imbalance (differential moments with and without motion) $$$\triangle\overrightarrow{M}$$$ induced by a rotational motion in the presence of diffusion gradients $$$\overrightarrow{G}$$$DW(t) play, is $$$\triangle\overrightarrow{M}=\int_{0}^{T}[\widehat{1}-\widehat{R}^{-1}(t)]\overrightarrow{G}$$$DW(t)dt, where $$$\widehat{R}(t)$$$ is the time dependent rotation matrix (T<TE). Assuming a rotation $$$\theta(t)$$$ about y-axis yields: $$\begin{bmatrix}{\triangle{M}_{x}} \\{\triangle{M}_{y}} \\{\triangle{M}_{y}} \end{bmatrix}=\int_{0}^{T}\begin{bmatrix}{1-cos(\theta(t))} & 0 & sin(\theta(t)) \\0 & 0 & 0\\{-sin(\theta(t))} & 0 & {1-cos(\theta(t))} \end{bmatrix} \begin{bmatrix}G_x^{DW}(t)\\G_y^{DW}(t)\\G_z^{DW}(t) \end{bmatrix}dt [1]$$with $$$\theta(0)=0$$$. Since the head can only rotate a few degrees over ~100ms TE, we can perform a second-order Taylor expansion in $$$\theta$$$and approximate $$$\theta(t)\cong{\omega}_{r}t+0.5{\alpha}_{r}t^{2}$$$, to obtain: $$\triangle{M}_{x}\cong\omega_{r}\int_{0}^{T}G_z^{DW}(t)tdt+\frac{1}{2}\int_{0}^{T}(\omega_r^2G_x^{DW}(t)+\alpha_{r}G_z^{DW}(t))t^{2}dt [2], $$ $$\triangle{M}_{z}\cong0 [3]$$Hence, head rotation during diffusion gradients creates: a. a first-order gradient moment, proportional to the rotational velocity perpendicular to the diffusion gradient and rotation axis; b. zero (no) gradient moment in the z-direction (rotation axis), in first order.Methods
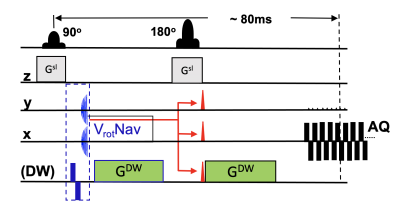
Figure 1 shows our initial implementation of the velocity-encoding navigator (vrotNav; blue block) in a spin-echo DWI sequence. Studies were done on a 3T Prisma scanner (Siemens). After exciting an axial slice (main diffusion sequence), a bipolar x-gradient (2*4ms; ±25mT/m) was played out followed by a brief spiral acquisition in the y-z plane (duration <3ms; k-space size 24*24; ±0.6mT/m*ms width). The velocity encoding module (bipolar gradient + readout) takes approximately 10ms, and fits into the typical dead time of the first TE/2 period. In the next iteration, the estimated velocities will be used to predict the current gradient imbalance for each excitation, using Eq. 2. A brief gradient blip will then be applied to reverse the predicated imbalance and recenter the echo in k-space (red arrows and blips in Figure 1).This navigator was repeated 120 times at TR=500ms, while a volunteer continuously rotated his head about the z-axis (L/R). Head motion was tracked independently using an MR-compatible motion tracking system (KinetiCor Inc). Since the head movement and scanning process are asynchronous, each DWI acquisition reflects a random (but known) rotational velocity. Since k-space is defined by gradient moments, the shift of the signal maximum (from iso-center) in the spiral (navigator) k-space reflects the motion-induced gradient imbalance due to the bipolar gradient (blue), which in turn can be converted into velocities using Equation [2]. Therefore, for each excitation, we determined the ky-shift (Δk) at signal maximum, which was converted into a rotational velocity. In parallel, we used the optical tracking system to calculate the z-rotational velocity during spiral readout.
Results
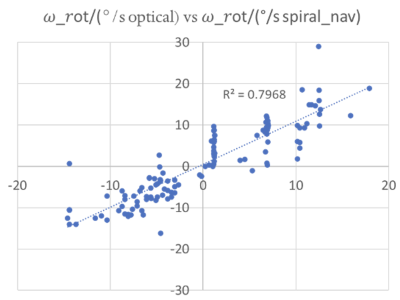
Figure 2 compares the measured rotational velocity from the navigator in °/s (x-axis) with the velocity from the optical tracking system (gold standard; y-axis). The navigator data were processed by converting the ky-value (gradient moment) at echo maximum into a velocity ωz (using the moment of the bipolar navigator gradient and Eq. 2). Their velocity navigator shows good agreement with the optical tracking system (r2≈0.80), and predicted the velocity from the optical system with an accuracy of 4.1°/s (residual standard deviation). Also, the selected navigator parameters can encode velocities | ωz | ≥ ±70°/s.Discussion
The proposed navigator can predict the actual velocity with an accuracy of ~4°/s over a wide range of velocities. Refinements in acquisition and processing should allow us to improve the accuracy to about 2°/s. The next step will be to add real-time correction of the gradient moment, using a gradient blip applied immediately before the EPI readout. The proposed velocity navigator promises reduced motion sensitivity of DWI acquisitions similar to that of 1st order gradient compensation [1-5], but with a much lower penalty in TE and ultimately SNR.Acknowledgements
This work was supported by NIH grant 1R01 DA021146 (BRP).References
1. Simonetti, O.P., R.E. Wendt, 3rd, and J.L. Duerk, Significance of the point of expansion in interpretation of gradient moments and motion sensitivity. J Magn Reson Imaging, 1991. 1(5): p. 569-77.
2. Ozaki, M., et al., Motion artifact reduction of diffusion-weighted MRI of the liver: use of velocity-compensated diffusion gradients combined with tetrahedral gradients. J Magn Reson Imaging, 2013. 37(1): p. 172-8.
3. Welsh, C.L., E.V. DiBella, and E.W. Hsu, Higher-Order Motion-Compensation for In Vivo Cardiac Diffusion Tensor Imaging in Rats. IEEE Trans Med Imaging, 2015. 34(9): p. 1843-53.
4. Pena-Nogales, O., et al., Optimized Diffusion-Weighting Gradient Waveform Design (ODGD) formulation for motion compensation and concomitant gradient nulling. Magn Reson Med, 2019. 81(2): p. 989-1003.
5. Lasic, S., et al., Motion-compensated b-tensor encoding for in vivo cardiac diffusion-weighted imaging. NMR Biomed, 2020. 33(2): p. e4213.
6. Li, Y., et al., Image corruption detection in diffusion tensor imaging for post-processing and real-time monitoring. PLoS One, 2013. 8(10): p. e49764.
7. Aksoy, M., et al., Real-time optical motion correction for diffusion tensor imaging. Magn Reson Med, 2011. 66(2): p. 366-78.
8. Herbst, M., et al., Prospective motion correction with continuous gradient updates in diffusion weighted imaging. Magn Reson Med, 2012. 67(2): p. 326-38.
9. Gumus, K., et al., Prevention of motion-induced signal loss in diffusion-weighted echo-planar imaging by dynamic restoration of gradient moments. Magn Reson Med, 2014. 71(6): p. 2006-13.
10. Herbst, M., et al., Prospective motion correction of segmented diffusion weighted EPI. Magn Reson Med, 2015. 74(6): p. 1675-81.
Figures
Fig. 1. The VrotNav is acquired immediately after excitation for providing estimates of rotational velocities perpendicular to the diffusion gradient. The red gradient blips after the refocusing pulse are used to rebalance the gradient moment based on the velocity navigator.
Fig. 2. Comparison of the measured rotational velocity from the navigator in °/s (x-axis) with the velocity from the optical tracking system (gold standard; y-axis). The velocity navigator can predict the ωz from the optical system (gold standard) with an accuracy of 4.1°/s.
DOI: https://doi.org/10.58530/2023/1823