Synopsis

Keywords: Quantitative Imaging, Quantitative Imaging

The phase unwrapping technique is only applicable to the fat-water separation problems with IP/OP acquisition. This work developed a transition approach that enabled phase unwrapping technique applicable to fat-water separation with arbitrary TE combination. By establishing intermediate variables, the proposed method provided an effective way to diminish the traditional “ambiguity” problem. To validate the concept, datasets acquired with various field strength, anatomical areas and acquisition types (two-point and six-point acquisition) were applied, and no fat-water swaps were observed.

Introduction

Fat-water separation problem can be solved by the well-established phase unwrapping algorithm¹, as long as the echo spacing between the multi-echoes results in kπ(k is odd integers) phase difference between fat and water^2-4. In this work, we generalize this procedure to fat-water separation with arbitrary echo combination.

Theory

The simplified chemical shift-encoded signal model could be expressed as:
$$$S_{n}=(\rho _{w}+\rho _{f}e^{-i2\pi f_{F}TE_{n}})e^{-i2\pi \phi TE_{n}}$$$ (1)
Where $$$S_{n}$$$ is the complex signal acquired at echo time $$$TE_{n}$$$, $$$f_{F}$$$is the chemical shift of fat with one-peak assumption, $$$\rho _{w}$$$ and $$$\rho _{f}$$$ are the fat and water intensities, π is the field inhomogeneity. $$$[\rho _{w}, \rho _{f}, \phi]$$$are the unknowns to be estimated from the model.
When the phase difference between fat and water is kπ(k is odd integers), the signal model becomes
$$$S_{1}=(\rho _{w}+\rho _{f})e^{-i2\pi \phi TE_{1}}$$$
$$$S_{2}=(\rho _{w}-\rho _{f})e^{-i2\pi \phi TE_{2}}=(\rho _{w}-\rho _{f})e^{-i2\pi \phi TE_{1}}p$$$ (2)
$$$S_{3}=(\rho _{w}+\rho _{f})e^{-i2\pi \phi TE_{3}}=(\rho _{w}+\rho _{f})e^{-i2\pi \phi TE_{1}}p^{2}$$$
... ...
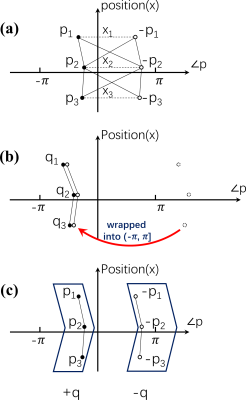
Where $$$p=e^{-i2\pi \phi \Delta TE}$$$ is defined as phasor related to field inhomogeneity. Both $$$[\rho _{w}, \rho _{f}, p]$$$ and $$$[\rho _{f}, \rho _{w}, -p]$$$ satisfy equations above, but the -p would lead to swap of fat and water. Assuming three neighboring pixels $$$x_{1}, x_{2}, x_{3}$$$ with their candidate phasors $$$\pm p_{1}, \pm p_{2}, \pm p_{3}$$$. There are eight possible combinations, $$$[p_{1}, p_{2}, p_{3}]$$$, $$$[p_{1}, p_{2}, -p_{3}]$$$, $$$[p_{1}, -p_{2}, p_{3}]$$$, $$$[-p_{1}, p_{2}, p_{3}]$$$, $$$[-p_{1}, -p_{2}, -p_{3}]$$$, $$$[-p_{1}, -p_{2}, p_{3}]$$$, $$$[-p_{1}, p_{2}, -p_{3}]$$$, $$$[p_{1}, -p_{2}, -p_{3}]$$$. However, the complication can be eliminated if all of the candidate phasors take power of 2 in this case. There remains only one combination $$$(p_{1}^{2}, p_{2}^{2}, p_{3}^{2})=(q_{1},q_{2},q_{3})$$$ of the powered phasor candidate. Considering possible 2π phase wrap, phase unwrapping algorithms were applied to the angle of intermediate variable $$$(q_{1},q_{2},q_{3})$$$ to guarantee a smooth change over the intermediate variable $$$q$$$.
For fat-water separation with arbitrary echo combination, the difference between two candidate solutions is no longer $$$e^{i\pi }$$$. However, the relationship between the true and aliased phasor solution can be approximated by:
$$$p_{a}=\left\{\begin{matrix} p_{t}e^{i2\pi f_{F}\Delta TE}& \rho_{w}>>\rho_{f} \\ p_{t}e^{-i2\pi f_{F}\Delta TE}& \rho_{w}<<\rho_{f} \\\end{matrix}\right. $$$ (3)
Although the relationship only holds in those “pure pixels” where $$$\rho_{w}>>\rho_{f}$$$ or $$$\rho_{w}<<\rho_{f}$$$, such approximation is valid as the fat fraction of the most anatomical regions is close to 0 or 100%.
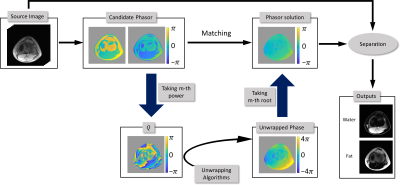
An intermediate variable is introduced by taking the m-th power of the original candidate phasors:

$$$Q=p^{m}$$$ (4)
Where $$$m=1/f_{F}\Delta TE$$$, then the $$$Q$$$ of aliased phasor solution becomes identical to that of the true phasor solution in these “pure pixels”:
$$$Q_{a}=\left\{\begin{matrix} p^{m}e^{i2\pi f_{F}\Delta TE}=Q_{t}& \rho_{w}>>\rho_{f} \\ p^{m}e^{-i2\pi f_{F}\Delta TE}=Q_{t}& \rho_{w}<<\rho_{f} \\\end{matrix}\right. $$$ (5)
Apparently, the difference between true and aliased solutions is eliminated after taking power of m as well. Pixels that do not satisfies $$$\left| \angle Q_{a}-Q_{t}\right|<0.05\pi $$$ are detected as “mixed pixels”. These pixels are excluded from the following steps and determined after all “pure pixels” are solved in the final step.
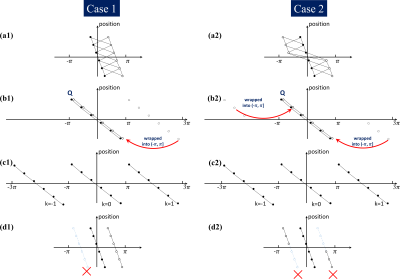
Unwrapping the phase of Q in the range of [-2πL,2πL] (L is a preset integer), the power roots of Q can be categorized intoT=2L+1 groups according to the index k: $$$\angle P_{k}= \frac{1}{m}(\angle Q+2k\pi ), k=-L,...,0,...,L$$$. Since m is not an integer in the general case, there might be T different combinations of solution after $$$\angle P_{k}$$$ is wrapped around back to (-π,π]. The proper choice of k could be determined by matching the possible solution to the original candidate phasor solutions with the cost function defined as:
$$$C(k)=\sum_{r}^{}min(|P_{1}(r)-P_{k}(r)|,|P_{2}(r)-P_{k}(r)|), k=-L,...,0,...,L$$$ (6)
Where r is the index of pixels, $$$P_{1}$$$ and $$$P_{2}$$$ is the original candidate solutions. The $$$P_{k}$$$ with the lowest cost function $$$C(k)$$$ is the final phasor solution. There would be two possible cases:
Case 1: For images containing only water or only fat regions, there would be two equally feasible solution combinations, the solution combination closer to 0 is selected as the final solution.
Case 2: For the images containing both water and fat regions, there would be only one solution combination that could be matched to the original candidate solutions. This unique solution combination is chosen as the final solution.
The flowchart of proposed method is illustrated in Figure 3.

Results

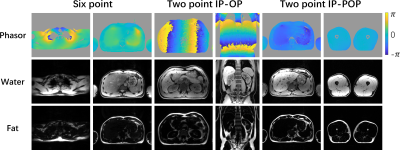
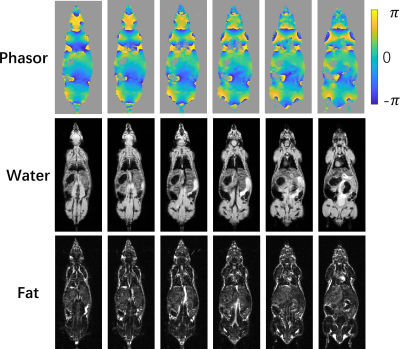
We acquired volunteer data on a clinical 3T scanner (uMR 790, Shanghai United Imaging Healthcare, Shanghai, China), and animal data on a 9.4T small animal scanner (uMR 930, Wuhan United Imaging Life Science Instrument, Wuhan, China). A 3D phase unwrapping algorithm SEGUE¹ was employed to unwrap the powered phasor images. For volunteer studies, TE1/∆TE was 1.5/1.52 ms for six-point acquisition, TE1/∆TE was 1.15/1.15 ms for IP/OP (In-Phase/Opposed-Phase) two-point acquisition, and TE1/∆TE was 1.38/0.93 ms for IP/POP (Partially Out-of-Phase) two-point acquisition. For animal experiments, the TE/∆TE was 0.78/1.19 ms. The results for volunteer study and animal experiments were shown in Fig.4 and Fig.5 respectively.

Discussion and Conclusion

This work generalized the phase unwrapping algorithm applicable to fat-water separation with arbitrary TE combination. To validate the concept, datasets acquired with various field strength, anatomical areas and echo numbers and echo combinations (two-point and six-point acquisition) were tested. No fat-water swaps were observed.
In conclusion, the proposed method shows successful application of phase unwrapping algorithm to the fat-water separation with arbitrary echo combination.

Acknowledgements

No acknowledgement found.