Synopsis

Keywords: Low-Field MRI, Image Reconstruction

In low-field and ultra-low-field MRI, concomitant fields can cause severe blurring and distortion in traditional Fourier reconstruction. We have developed an improved image reconstruction framework based on our previously published method that uses a frequency–space formulation. It provides more accurate reconstruction results with the cost of increased computation time. Known inhomogeneity and other field nonidealities can be incorporated into the model to improve the quality of the reconstruction. The framework will be published as open source.

Introduction

In low-field and ultra-low-field MRI, the bandwidth of the Larmor frequencies is relatively large compared to the mean frequency of operation. While this helps eliminate some image artefacts¹, it also means that the field gradients cannot be considered uniform as Maxwell’s fourth equation in current-free regions requires that any magnetic field gradient $$$∂B_z/∂x$$$ is associated with a concomitant magnetic field gradient $$$∂B_x/∂z$$$ of equal magnitude. Traditional Fourier reconstruction would thus result in severe blurring and distortion².

Methods

We have implemented an improved image reconstruction framework in Python, based on our previously published method² that uses a frequency–space formulation: In the first stage, the signal amplitude and phase are estimated on equidistant frequency isocontours by applying the Fourier transform in the frequency-encoding direction. In the second stage, the phase-encoding weightings along these isocontours are combined into a matrix. The magnetization distribution is then computed by solving a matrix equation for each of the frequency isocontours, and the three-dimensional image is reconstructed by interpolating the voxel values in a uniform grid. To be as general-purpose as possible, the reconstruction framework takes the MRI coil configuration as a parameter. For each MRI coil, the framework can use either an ideal or a measured magnetic field profile or compute the field profile based on the coil geometry.

Results

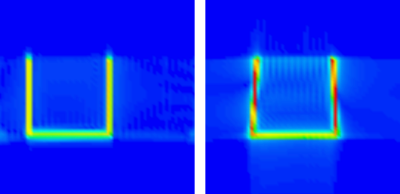
The reconstruction results from a simulated signal are shown in figure 1. Most of the computation time is spent composing the matrix. On a modern laptop with an Apple M1 Pro processor and 32 GiB of memory, it took a few seconds for a small matrix, and several minutes for a 64 × 64 × 64 matrix. The matrix has in total $$$N_q (N_{PE1} − 1) (N_{PE2} − 1) N_{PE1}N_{PE2}$$$ elements, where $$$N_{PE1}$$$, and $$$N_{PE2}$$$ are the number of phase encoding steps in each direction and $$$N_q$$$ is the number of quadrature points per grid cell. It can be computed in advance for a given matrix size, field of view, and coil configuration.

Discussion

From image quality perspective, our frequency–space image reconstruction framework performs better than traditional Fourier reconstruction in low and ultra-low fields. However, this comes at the cost of increased computation time. The computational performance of our first, naive implementation is acceptable on small image matrices. For large matrices, the algorithms need to be improved and possibly written in native code.

Conclusion

Compared to high-field MRI, the benefits of low-field MRI include potentially lower cost, better mobility, better sensitivity to hyperpolarized contrast agents, and immunity to inhomogeneity and susceptibility problems^1,3-5. However, combining strong gradients with traditional Fourier reconstruction is not practical in low-field MRI because of the distortions resulting from concomitant fields. With our reconstruction framework, low-field MRI can provide geometrically accurate images even at higher gradient strengths.

Acknowledgements

No acknowledgement found.