Synopsis

Keywords: Quantitative Imaging, Fat

This work proposes a new model for solving the water-fat separation problem with bipolar acquisition, which allows us for reducing the acquisition time and computing accurate PDFF without any special concerns about phase corrections. We solve jointly two water-fat separation problems for even and odd echoes, under the assumption that the concentrations are different, but considering the same field map and $$$R_2^*$$$. Bland Altman plots and linear regression show excellent performance for PDFF estimation in 8 healthy volunteers.

Introduction

Water-fat separation techniques estimate the water and fat concentrations jointly with the field map and $$$R_2^*$$$¹. Although unipolar readout is a very robust sequence for Proton Density Fat Fraction (PDFF) estimation, a bipolar readout shortens the scan time by reducing the echo spacing². This is useful for breath-hold acquisitions typically used in the liver. However, using bipolar readouts becomes challenging due to the phase inconsistencies between even and odd echoes. Some of them can be corrected by shifting the k-space center of even echoes², however other effects, such as concomitant gradients and eddy currents are harder to overcome³. They have been addressed using an extra non-linear phase term that changes its polarity between even and odd echoes⁴ and interleaved acquisitions⁵. In this work we propose a new method for solving the water-fat separation problem with bipolar acquisition, allowing to compute accurate PDFF without any special concerns about phase corrections.

Methods

We jointly solve two water-fat separation problems for even and odd echoes, assuming that the concentrations are different but the field map and $$$R_2^*$$$ are identical. The conventional model of water-fat separation problem can be defined as follows¹, $$ s(t) = (\rho_w + \rho_f \sum_{p=1}^{n_p} \omega_p \mathrm{e}^{i2\pi f_p t}) \mathrm{e}^{i2 \pi \xi t} ,$$
where $$$\rho_w$$$ and $$$\rho_f$$$ are the complex water and fat concentrations, $$$f_p$$$ and $$$\omega_p$$$ the frequencies and relative amplitudes of the pre-calibrated $$$n_p$$$-peak fat spectrum⁶, and $$$\xi = \phi + i 2\pi R_2^*$$$, where $$$\phi$$$ and $$$R_2^*$$$ denotes the field map and the signal decay.
Considering $$$n$$$ echo times, the matrix form of the previous problem is given by $$s = W(\xi)M\rho,$$ where $$$s$$$ is the signal vector, $$$W(\xi) = \mathrm{diag}(\mathrm{e}^{i2\pi t_1}, …, \mathrm{e}^{i2\pi t_n})$$$, $$$\rho$$$ is the concentration vector and,
$$M := \begin{bmatrix} 1 & \sum\limits_{p=1}^{n_p} \omega_{p} \text{e}^{2\pi i f_p t_1} \\ \vdots & \vdots \\ 1 & \sum\limits_{p=1}^{n_p} \omega_{p} \text{e}^{2\pi i f_p t_{n}}\end{bmatrix}.$$
Considering the aforementioned assumptions, the matrix $$$M$$$ can be reformulated as follows,
$$M := \begin{bmatrix} 1 & 0 & \sum\limits_p^{n_p} \omega_{p} \text{e}^{i 2\pi f_p t_1} & 0 \\ 0 & 1 & 0 & \sum\limits_{p=1}^{n_p} \omega_{p} \text{e}^{i 2\pi f_p t_2} \\ 1 & 0 & \sum\limits_p^{n_p} \omega_{p} \text{e}^{i 2\pi f_p t_3} & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 1 & 0 & \sum\limits_{p=1}^{n_p} \omega_{p} \text{e}^{i 2\pi f_p t_n} \end{bmatrix},$$
and $$$\rho=[\rho_w^+ \rho_w^- \rho_f^+ \rho_f^-]^T$$$, with $$$ +$$$ and $$$ - $$$ denoting the readout gradient polarity.
We solve the following optmization problem $$\begin{equation*} \begin{aligned} & \underset{\xi}{\mathrm{min}} & & \frac{1}{2}\sum\nolimits_{v \in V} ||{P(\xi_v)s}||_2^2 + \beta_1 \mathrm{TV}(\text{Im}(\xi))\\ & \mathrm{s.t.} & & \forall\,v\in V:\,\, ||{\nabla \text{Re}(\xi_v)}||_2 \leq \varepsilon_\Phi,\,\, 0 \leq \text{Im}(\xi_v) \end{aligned}\end{equation*},$$
where, $$$P(\xi) := W(\xi) (I_n - M M^+) W(-\xi)$$$, $$$M^+$$$ is the pseudo-inverse of $$$M$$$, $$$v$$$ denotes one voxel, the first constraint is an smoothing term for the field map to prevent swaps and the second one is the $$$R_2^*$$$ non-negativity constraint. This problem can be solve using Gauss Newton Trust Region⁷, combining ADMM⁸ and FISTA⁹.
Concentrations are obtained by solving the least square problem $$$ \rho(\xi) = M^+ W(-\xi) s$$$. Increasing the number of concentrations decreases the SNR of the estimations, deteriorating the PDFF. This is compensated by using all the concentrations to estimate the PDFF,
$$PDFF = \frac{|\rho_f^+| + |\rho_f^-|}{|\rho_f^+| + |\rho_f^-| + |\rho_w^+| + |\rho_w^-|}.$$

To validate our proposal, we prospectively acquired 8 healthy volunteers in a 1.5T Philips Achieva scanner. As ground truth, we used a 6-echoes gradient echo unipolar acquisition with $$$\Delta$$$TE/TE1 2.1/1.3, flip angle 10°, TR 30ms, voxel size 2x2x8 mm. Water/fat separation was performed using graph cuts¹⁰. Bipolar acquisitions were identical to the latter, except for the reduced $$$\Delta$$$TE to 1.1 ms.
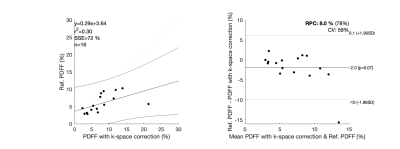
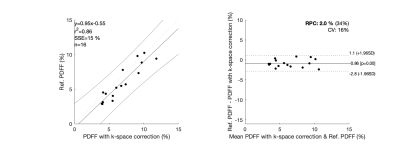
For statistical analysis we use linear regression, correlation and Bland Altman (BA) plots of the median PDFF, considering two regions of interest (ROIs), in the left and right hepatic lobes.

Results

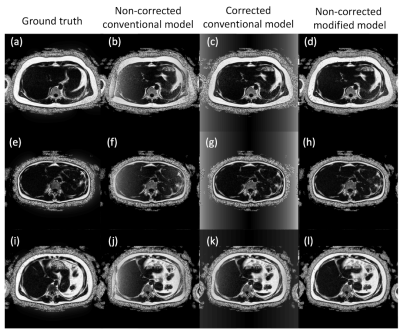
Non-corrected data lead to wrong PDFF estimations (Fig.1 (b), (f), (j)). Results with k-space correction (Fig. 1 (c), (g), (k)) showed an improvement in PDFF appealing, however, the performance was quantitively poor, with an $$$r^2$$$ correlation coefficient of 0.30 and BA plots showed a considerable bias and CV of 59%. Our new water-fat model (Fig. 1 (d), (h), (l)) improved the $$$r^2$$$ correlation coefficient to 0.86, reduced the bias to 0.86% of fat, showed a good LOA, and the CV was 16%.

Discussion

Our new water-fat separation model allows us for computing accurate PDFF without any concern about the phase inconsistencies produced by bipolar readout, and therefore, achieving shorter scan times assuring the necessary number of echoes for a good quantification¹¹. Instead of adding non-linear unknowns to the problem, we introduced additional concentrations, which are easier to estimate. In that sense, all the phase inconsistencies are expressed by the phase of these concentrations. A constraint that our model missed is that the concentrations have the same magnitude. We have not found a straightforward way to impose that constraint. The major cost paid by our model is the SNR decay for introducing more variables. We compensate that by combining the magnitudes of all variables in the final PDFF estimation.

Conclusion

Novel water-fat separation model allows for obtaining accurate PDFF with bipolar readout acquisitions and without any special concern about the phase of even and odd echoes. Future work includes analyzing subjects with higher-fat liver content.

Acknowledgements

This work was funded by ANID – Millennium Science Initiative Program – ICN2021_004, ANID Fondecyt 1181057, ANID Fondecyt 1191710, ANID Fondecyt 1231535, ANID–PIA–ACT 192064 and PUENTE grant 2022-14 VRI, PUC. C.A. was partially funded by ANID Fondecyt Postdoctorado 2019 #3190763. C.S-L was funded by ANID Fondecyt 1211643 and Centro Nacional de Inteligencia Artificial CENIA, FB210017, BASAL, ANID. J.M was funded by the National Agency for Research and Development (ANID) / Scholarship Program / DOCTORADO BECAS CHILE/2020 – 21210665. H. M. thankfully acknowledges thee financial support of the project ANID - FONDECYT Postdoctorado #3220266.