Synopsis

Keywords: Quantitative Imaging, Image Reconstruction

This work presents a simulation study on the differences between data from accelerated T2 mapping experiments vs T2w imaging studies. Subspace constrained and model-based reconstruction were tested on trajectories that exhibited narrow k-space sampling at each window, energy differences across echoes related to the k-space collected by each echo, and small total data size. Energy differences had the largest impact on T2 map reconstruction, and both methods were unsuitable for reconstructing T2w data that combined all features. This highlights the need for tailored reconstruction approaches, such as e-CAMP, to reconstruct T2 maps from T2w data.

Introduction

Reconstructing quantitative T2 maps from T2w image data could harmonize clinical images acquired at different sites for deep learning and other analyses. There are conceptual similarities between T2w data and accelerated T2 mapping data, so it is plausible that methods successful for generating T2 maps from the latter could be applied to T2w data. (1-4) However, reconstructing a T2 map from actual T2w image data presents significant novel challenges, and our results find that standard methods do not perform well on T2w data.

This work presents a simulation study on how sampling strategy across echoes impacts T2 map reconstruction. Accelerated T2 mapping experiments in the literature typically use sampling strategies that broadly and equitably sample k-space in each window. In contrast, clinical T2w image data provides a concentrated sampling pattern at each echo. When the pattern is concentrated near the center of k-space, the data is very high intensity. When the pattern is concentrated far from the center of k-space, the data is very low intensity. These biases in signal intensity are unrelated to TE-dependent magnetization brightness and obscure T2 decay. Finally, the total size of a T2w dataset is lower than many accelerated T2 mapping studies reported in the literature. Together, these features cause highly effective algorithms, including model-based and subspace-constrained reconstruction, to fail. However, it is unclear which aspect of T2w data contributes to the observed performance.

e-CAMP is a reconstruction algorithm designed to overcome these obstacles and to produce high quality T2 maps directly from a T2w image acquisition. (5-6) e-CAMP uses a linearized penalty term for model consistency, a phase conjugacy constraint, and a growing algorithm which gradually incorporates the edges of k-space. Isolating which features of the T2w sampling pattern are challenging for other methods may elucidate what drives the better performance of e-CAMP on T2w data.

Methods

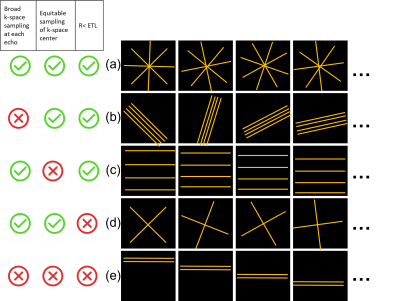
In this simulation study, two successful algorithms, namely model-based and subspace constrained reconstruction, are applied to:
(a) Data with interleaved radial sampling across echoes, which provides equtibale signal energy and a broad sampling of k-space at each echo, ETL=8, R=4
(b) Data that acquires a different blade at each echo, providing equitable signal energy but a narrow sampling of k-space at each echo, ETL=8, R=4
(c) Data with interleaved Cartesian sampling across echoes, which creates some signal energy differences across echoes despite the broad sampling of k-space, ETL=8, R=4
(d) Data with interleaved radial sampling, but where to total data size corresponds to a single k-space (ETL=8, R=8)
(e) T2w data, which combines all three challenges: a narrow sampling of k-space at echo, strong energy biases across echoes related to which part of k-space is sampled, and a minimal data size (ETL=8, R=8)

Figure 1 shows a schematic of the different sampling patterns. Model-based and subspace constrained reconstructions were performed using the Berkeley Advanced Reconstruction Tool (BART) package. (7-8) Subspace constrained reconstruction used 4 basis functions without regularization. Model-based reconstruction used the number of Newton steps (<12) and regularization (L1, L2, or none) which optimized performance for each trajectory. An unconstrained reconstruction was also performed as a reference.

Results

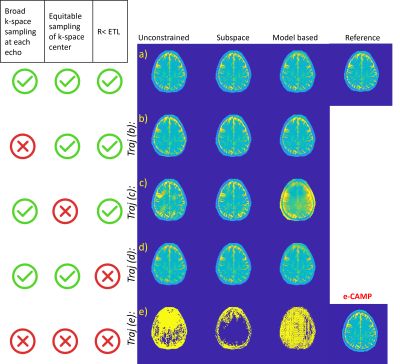
Figure 2 shows the T2 maps associated with each sampling pattern for unconstrained, subspace-constrained, and model-based reconstruction. Both interleaved spokes (a) and PROPELLER-like sampling (b) result in relatively good reconstructions, so sampling a limited span of k-space at each echo appears to not be a major challenge to these algorithms.

Panel 2c introduces slight energy biases in the data since k=0 is sampled only at echoes 3 and 7. This deviation from monoexponential decay is well handled by subspace constrained reconstruction, but is more problematic in model-based reconstruction. Reducing the dataset to the equivalent of a single radial k-space (2d) increases blur for constrained and unconstrained reconstructions but does not dramatically bias T2 maps.

Panel 2e shows the performance of each method on T2w data, which combines concentrated and energy-biased sampling with a minimal dataset. As can be seen, none of these methods are able to resolve a meaningful T2 map. An e-CAMP reconstruction of this data is shown for comparison.

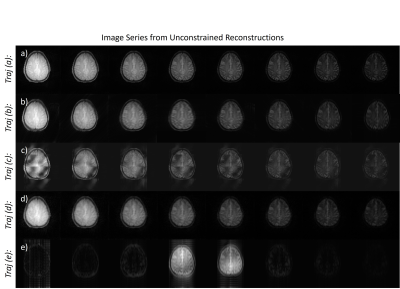
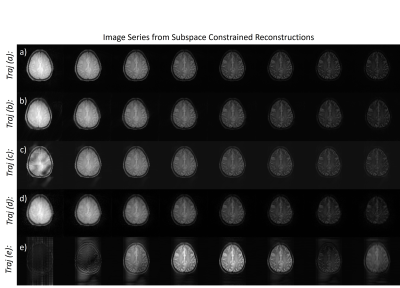
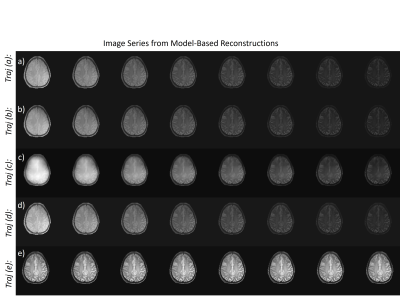
Figures 3-5 show the image series associated with each sampling pattern for unconstrained, subspace-constrained and model-based reconstruction, respectively. In particular, the unconstrained reconstruction of T2w data (3e) highlights the strong energy biases associated with this k-space sampling. The subspace constrained reconstruction (4e) allows for reasonable fitting of the natural brightness pattern inherent to T2w data, but the underlying T2 is still lost. Model-based reconstruction enforces strict monoexponential decay, so sampling patterns that do not equitably sample the center of k-space (5c and 5e), show the greatest inaccuracies in the image series.

Conclusion

From these simulations, it appears that patterns that do not equitably sample the center of k-space at each echo are more challenging for reconstruction. Taking this into account, e-CAMP initializes by taking only those echoes that are near the center of k-space and gradually grows the solution to incorporate all the data. Our simulation suggests this is a key reason for the accuracy of e-CAMP T2 maps generated from T2w data.

Acknowledgements

No acknowledgement found.