Synopsis

Keywords: Quantitative Imaging, Machine Learning/Artificial Intelligence

We proposed a new method that integrates an adapted generative network image prior and subspace modeling for accelerated MR parameter mapping. Specifically, a formulation is introduced to synergize a subspace constraint, a subject-specific generative model-based image representation and joint sparsity regularization. A pretraining using public database plus subjective specific network adaptation strategy is used to construct an accurate representation of the unknown contrast-weighted images. An efficient alternating minimization algorithm is used to solve the resulting optimization problem. The improved reconstruction performance achieved by the proposed method over subspace and sparsity constraints was demonstrated in a T₂ mapping experiment.

Introduction

Quantitative MR parameter mapping (qMR) is playing an ever-important role in tissue characterization and pathological analysis^1-2. One major challenge for clinical application of qMR is the prolonged acquisition due to the need to acquire multiple contrast-weighted images for parameter estimation. Image reconstruction from sparsely sampled data has demonstrated excellent potential in accelerating qMR. For example, constrained reconstructions using sparse representations^3-4, low-rank matrix/tensor models^5-8, and their combinations have been well recognized. Recently, deep learning (DL)-based methods have provided new ways to formulate qMR problems and to introduce data adaptive priors. The majority of existing DL methods rely on supervised training using a large number of fully-sampled datasets^9-10. To address the data scarcity issue, self-supervised learning strategies have also shown promise^11-12. In this work, we proposed a new method that integrates a state-of-the-art generative image model and subspace model for qMR reconstruction. We introduced a pretraining plus subject-specific adaptation strategy for learning an accurate generative adversarial network (GAN)-based image representation and used it as an adaptive spatial constraint in a subspace-based reconstruction. Our method does not require end-to-end supervised training and allows flexible integration of other constraints, e.g., joint-sparsity, to further improve the reconstruction. We demonstrated the effectiveness of our method using T₂ mapping experiments.

Theory and Methods

Generative prior constrained subspace reconstruction
We formulate the qMR reconstruction problem as follows:
$$\hat{\mathbf{U}},\hat{\mathbf{w}}_{\text {rec}}=\text{arg}\underset{\mathbf{U},\mathbf{w}}{\operatorname{min}}\sum_{c=1}^{N_c}\left\|\mathbf{d}_{\mathbf{c}}-\boldsymbol{\Omega}\left(\mathbf{F S}_{\mathbf{c}}\mathbf{U}\hat{\mathbf{V}}\right)\right\|_2^2+\lambda_1\left\|\mathbf{U} \hat{\mathbf{V}}-\boldsymbol{G}_{\boldsymbol{\hat{\theta}}}(\mathbf{w})\right\|_F^2+\lambda_2 R(\mathbf{U}\hat{\mathbf{V}}),\text{(1)}$$
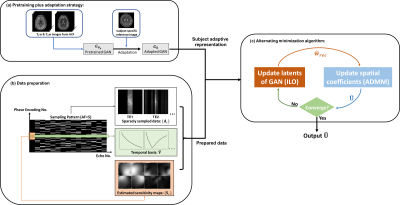
where $$$\boldsymbol{\Omega},\mathbf{F},\mathbf{S}_{\boldsymbol{c}},\mathbf{d}_{\mathbf{c}},\hat{\mathbf{V}}$$$ denote the $$$(\mathrm{k},\mathrm{p})$$$-space sparse sampling mask ( $$$\mathrm{p}$$$ denoting the parameter dimension, e.g., TE in T₂ mapping), Fourier operator, coil-dependent sensitivity maps, measured multichannel data, and a predetermined temporal basis, respectively. The first term in Eq. (1) is the well-established subspace/low-rank model, and $$$R(.)$$$ can be a hand-crafted regularization term, e.g., promoting joint sparsity^4,5. The second term introduces a GAN-based image-manifold constraint. One key assumption is that for a well-trained and adapted GAN-based image model with fixed parameter $$$\hat{\boldsymbol{\theta}}$$$, the contrast variations in the image sequence can be accurately accounted for by updating only the low-dimensional latent space variable $$$\mathbf{w}$$$ (referred to as the latents). Here, we propose a pretraining plus subject-specific adaptation strategy to construct $$$\boldsymbol{G}_{\hat{\boldsymbol{\theta}}}$$$ without needing a large scale T₂ mapping dataset for training.

Adaptive generative image model
To construct a generative model that can capture geometry and contrast variations in brain MRI, we first pretrain a StyleGAN2¹³(excellent high-resolution image generation capability), on the HCP database¹⁴ ( ~100K T₁w&T₂w images). Assume that a high-resolution reference image $$$\mathbf{x}_{\mathrm{p}}$$$ is available in a parameter mapping experiment (not necessarily the same contrast), we can adapt the pretrained $$$\boldsymbol{G}_{\boldsymbol{\theta}_{\mathbf{p}}}(.)\left(\boldsymbol{\theta}_{\mathbf{p}}\right.$$$ denotes the network parameters) to $$$\mathbf{x}_{\mathbf{p}}$$$ by updating both the network parameters and latents $$$\mathbf{w}$$$ as:
$$\hat{\mathbf{w}}, \hat{\boldsymbol{\theta}}=\text{arg}\underset{\mathbf{w},\boldsymbol{\theta}}{\operatorname{min}}\left\|G_{\boldsymbol{\theta}}(\mathbf{w})-\mathbf{x}_{\mathbf{p}}\right\|_2^2+\alpha\left\|\boldsymbol{\theta}-\boldsymbol{\theta}_{\mathbf{p}}\right\|_2^2.\text{(2)}$$
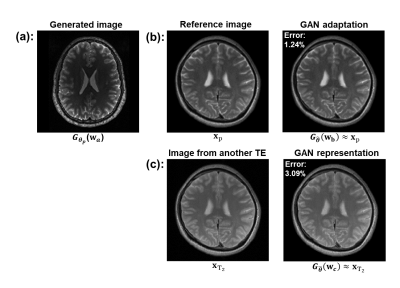
The second term penalizes large deviation of the adapted network from the pretrained one. This pretraining+adaptation strategy produces an effective GAN-based image prior for which updating only the low-dimensional latents can accurately account for contrast variations, as shown in Fig. 1. A strategy that uses a T₁-to-T₂ image translation network to generate reference image for constrained reconstruction was previously proposed¹⁵. In our method, the network serves as an image representation that is dynamically updated in a unified optimization process (Eq. (1)).

Algorithm
With the adapted $$$\boldsymbol{G}_{\hat{\boldsymbol{\theta}}}$$$ and $$$R(.)=\|\mathbf{D U \hat { V }}\|_{\mathbf{2,1}}$$$ ($$$\mathbf{D}$$$ being a finite difference operator⁵ ), we solve Eq. (1) using an alternating minimization algorithm. More specifically, the algorithm alternates between updating the latents $$$\mathbf{w}$$$ and spatial coefficients $$$\mathbf{U}$$$, i.e.,$$\begin{gathered}\hat{\mathbf{w}}_{rec}^{i+1}=\text{arg}\underset{\mathbf{w}}{\operatorname{min}}\left\|\hat{\mathbf{U}}^i\hat{\mathbf{V}}-G_{\hat{\boldsymbol{\theta}}}(\mathbf{w})\right\|_F^2;\text{(3)}\\\hat{\mathbf{U}}^{i+1}=\text{arg}\underset{\mathrm{U}}{\operatorname{min}} \sum_{c=1}^{N_c}\left\|\mathrm{~d}_{\mathbf{c}}-\Omega\left(\mathbf{F S}_{\mathrm{c}}\mathbf{U}\hat{\mathbf{V}}\right)\right\|_2^2+\lambda_1\left\|\mathbf{U} \hat{\mathbf{V}}-G_{\hat{\theta}}\left(\hat{\mathbf{w}}_{\text{rec }}^{i+1}\right)\right\|_F^2+\lambda_2\|\mathbf{X}\|_{2,1}, \text{s.t.}\mathbf{X}=\mathbf{DU\hat{\mathbf{V}}};\text{(4)}\end{gathered}$$
where $$$i$$$ is the iteration index and $$$\mathbf{X}$$$ an auxiliary variable for handling the $$$l_{2,1}$$$-norm. We used the intermediate layer optimization (ILO) algorithm¹⁶ to solve (3) and ADMM¹⁷ to solve (4). The algorithmic workflow is illustrated in Fig. 2.

Results

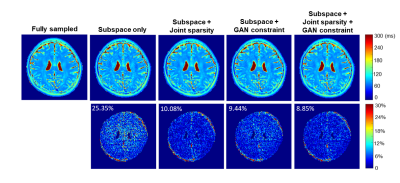
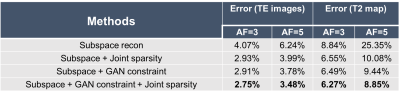
We evaluated the proposed method using in vivo T₂ mapping data (with local IRB approval). Data were acquired using a multi-spin-echo sequence on a 3T scanner using a 12-channel head coil: 16 echoes, $$$\mathrm{TE}_1=8.8 \mathrm{~ms}$$$ and echo spacing $$$\Delta \mathrm{TE}=8.8 \mathrm{~ms}$$$. The proposed method was benchmarked against a state-of-the-art joint subspace and sparsity constrained reconstruction using retrospectively under-sampled data at different acceleration factors (AFs). The central 8 k-space lines were acquired at all TEs for subspace determination^5,6, and the central k-space was fully sampled at 1^st TE (coverage depending on AFs, e.g., 32 $$$k_y$$$'s for AF = 4) for coil sensitivity estimation by ESPIRiT¹⁸.
For T₂ mapping, we used a sum-of-squares (SoS) combination of images across all TEs from an initial subspace reconstruction as $$$\mathbf{x}_{\mathrm{p}}$$$ for adapting the pretrained StyleGAN2 (Eq. (2)); note that the SoS image exhibits negligible aliasing even at high AFs. While a high-resolution T₁w image can also be used, the strategy here may eliminate additional acquisitions. Fig. 3 compares the reconstruction from different methods at AF=5, demonstrating the superior performance of the proposed method, especially when combining joint sparsity constraint. More quantitative comparisons are shown in Table 1. The proposed method consistently achieved lower errors at different AFs.

Conclusion

We proposed a novel reconstruction method for qMR that integrates subspace modeling and a subject-adaptive GAN-based image representation. We validated the accuracy of our pretrained and adapted StyleGAN2 in capturing contrast variations, and demonstrated improved reconstruction by the proposed method for accelerated T₂ mapping.

Acknowledgements

This work was supported in part by NSF-CBET-1944249 and NIH-NIBIB-1R21EB029076A