1619
B0 Dependence of Magnetization Transfer and Spin Relaxation Times1Dept. of Radiology, NYU Langone, New York, NY, United States
Synopsis
Keywords: Quantitative Imaging, CEST & MT, MR Fingerprinting, qMT, Low field, B0-field dependance
We demonstrate an approach to quantify unconstrained MT parameter mapping and utilized this approach to study the magnetic field dependence of the relaxation and MT parameters. The largest field dependence was observed in the longitudinal relaxation rate of the semi-solid spin pool.Introduction
The $$$T_1$$$-contrast is of tremendous clinical value, in particular for neuro-imaging. Recently publications1,2,3,4 have shifted our understanding of the underlying relaxation mechanisms by pointing at magnetization transfer (MT)5 as the main contributor. Key to this new understanding is Helm's1 observation that the semi-solid spin pool, i.e. the pool comprising all protons bound in macromolecules, has a longitudinal relaxation rate $$$R_1^f\approx3$$$/s, which is much faster than $$$R_1^f\approx0.5$$$/s of the free pool, and both those values differ substantially from the commonly assumed apparent $$$R_1^a\approx1$$$/s, all measured at 3T. Wang et al.6 explored the change $$$R_1^s$$$ over a range of clinical field strengths. Due to the challenging nature of the $$$R_1^s$$$-$$$R_1^f$$$-separation, they fixed $$$R_1^f=0.4$$$/s in their fits. The advent of MR-Fingerprinting7 and subsequent developments, such as the hybrid state8 have boosted the encoding potential of MRI pulse sequences, which enabled the voxel-wise disentanglement of individual relaxation mechanisms9. Here, we utilize those advances to replicate the work of Wang et al.6 w/o any constraints on $$$R_1^f$$$. We fit an unconstrained two-pool MT10 model to hybrid-state data measured at 0.55T, 1.5T, and 3T.Methods
For all three field strengths, a balanced hybrid-state sequence was used to encode the bio-physical parameters8,9. We numerically optimized the flip angle and duration of a train of rectangular RF-pulse to minimize the relative Cram\'er–Rao bound (CRB) of all bio-physical parameters as described in Ref. 9 and 12. Separate optimizations for each field strength were performed with their respective relaxation rates for white matter (WM)6 and the specific hardware limitations of each scanner, such as SAR and peak voltage. The sequence utilizes 3D radial k-space readout with a nominal isotropic resolution of 1.6mm and TR=3.5ms. Due to uncertainty in the expected signal-to-noise ratio (SNR) at lower fields, a long scan time of 36mins was chosen.The data was directly reconstructed in a low rank subspace14,15,16 using locally low-rank regularization16. Subsequent voxel-wise parameter fitting was performed with a neural network for time efficiency17.The fitted model describing the spin dynamics of the semi-solid spin pool utilized the generalized Bloch model12 assuming a super-Lorentzian lineshape. It fits a complex-valued scaling factor $$$M_0$$$ and the six biophysical parameters of the two-pool model. For 0.55T, homogeneous B$$$_0$$$ and B$$$_1$$$ fields were assumed, but at 1.5T and 3T we also fitted those field variations. In agreement with our institution's IRB, the same healthy volunteer was scanned at a 0.55T (ramped down Aera, Siemens), a 1.5T (Sola, Siemens) and a 3T (Prisma, Siemens) using the vendor-provided head coils. At 3T an additional MP-RAGE was acquired for as an anatomical reference, which was used for automated brain segmentation using FreeSurfer18 All scans were registered19,20 to the 3T scan during post-processing.
Results and Discussion
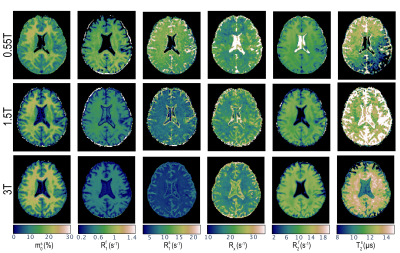
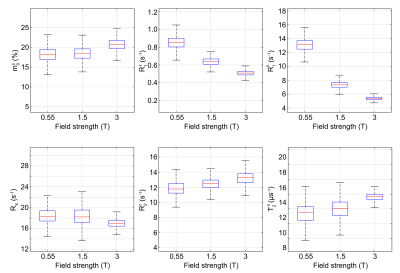
Fig.1 shows a transverse slice from the whole brain data set for all three field strengths and all 6 bio-physical parameters. The columns show the fractional size of the semi-solid spin pool (m$$$_0^s$$$), the respective longitudinal relaxation rates of the two pools ($$$R_1^f$$$,$$$R_1^s$$$), the exchange rate ($$$R_x$$$), and respective transverse relaxation rate/time ($$$R_2^f$$$,$$$R_2^s$$$). An entire-WM ROI is analyzed in Fig.2. Our principal finding is that $$$R_1^s$$$ shows the largest field strength dependence with $$$R_1^s \propto B_0^{-0.71}$$$. This largely confirms the findings in Ref. 6, though we measure a smaller exponent compared to the relation R$$$_1^s \propto B_0^{-1}$$$ reported by Wang et al.6. Our fits do not restrict $$$R_1^f$$$ and we do indeed observe a $$$B_0$$$ dependence of R$_1^f$, but this dependence is much weaker compared to R$$$_1^s$$$. The R$$$_1^f$$$-dependence was neglected in Ref. 6, which could explain the difference in the fitted exponent.The other parameters appear to be mostly independent of $$$B_0$$$ with the exception of $$$R_2^f$$$, where we do observe an approximately linear increase with $$$B_0$$$ in WM and an approximately quadratic increase in the iron-rich globus pallidus (not shown here). Estimates for cerebrospinal fluid are erroneous since the sequence was not tailored for the quantification relaxation times in this range. Lastly, a anterior-posterior gradient can be seen in $$$R_1^s$$$ and $$$T_2^s$$$ at 0.55T. These are likely artefacts cause by variation in the local $$$B_1$$$-field.
Conclusion
We demonstrated an approach to quantify unconstrained MT parameter mapping and utilized this approach to study the magnetic field dependence of the relaxation and MT parameters. The largest field dependence was observed in the longitudinal relaxation rate of the semi-solid spin pool. Future work will entail an analysis of the differing information content of $$$T_1$$$ weighted images at different field strengths.Acknowledgements
This work was supported by grant NIH/NIBIB R21 EB027241 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research, a NIBIB Biomedical Technology Resource Center (NIH~P41 EB017183).References
[1]Gunther Helms and Gisela E Hagberg. In vivo quantification of the bound pool T 1 in human white matter using the binary spin–bath model of progressive magnetization transfer saturation. Physics in Medicine and Biology, 2009.
[2] Peter van Gelderen, Xu Jiang, and Jeff H. Duyn. Effects of magnetization transfer on T1 contrast in human brain white matter. NeuroImage, 2016.
[3] Alan P. Manning, Alex L. MacKay, and Carl A. Michal. Understanding aqueous and non-aqueous proton T1 relaxation in brain. Journal of Magnetic Resonance, 2021.
[4] Alexey Samsonov and Aaron S. Field. Confounding of Macromolecularand Paramagnetic Tissue Content in Quantitative MTI Remedied by Explicit Estimation of Bound Pool Relaxation. In Proc. Intl. Soc. Mag. Reson. Med., 2021.
[5] Steven D. Wolff and Robert S. Balaban. Magnetization transfer contrast(MTC) and tissue water proton relaxation in vivo. Magnetic Resonancein Medicine, 10(1):135–144, 1989.
[6] Yicun Wang, Peter van Gelderen, Jacco A. de Zwart, and Jeff H. Duyn.B0-field dependence of mri T1 relaxation in human brain. NeuroImage, 2020.
[7] Dan Ma, V Gulani, N Seiberlich, K Liu, JL Sunshine, JL Duerk, and MA Griswold. Magnetic resonance fingerprinting. Nature, 2013.
[8] J Assländer, DS Novikov, R Lattanzi, DK Sodickson, and MA Cloos. Hybrid-state free precession in nuclear magnetic resonance. CommunPhys, 2019.
[9] Sebastian Flassbeck and Jakob Assländer. Quantitative magnetization transfer: Estimation of the Semi-Solid Spin Pool’s T1. In Proc. Intl. Soc. Mag. Reson. Med., 2019.
[10] R. Mark Henkelman, Xuemei Huang, Qing-San Xiang, G. J. Stanisz,Scott D. Swanson, and Michael J. Bronskill. Quantitative interpretation of magnetization transfer. Magnetic Resonance in Medicine, 1993.
[11] Jakob Assländer, Cem Gultekin, Andrew Mao, Xiaoxia Zhang, Quentin Duchemin, Kangning Liu, Robert W Charlson, Timothy Shepherd, Carlos Fernandez-Granda, and Sebastian Flassbeck. Rapid quantitative magnetization transfer imaging: utilizing the hybrid state and the generalized bloch model, 2022.
[12] Jakob Assländer, Cem Gultekin, Sebastian Flassbeck, Steffen J Glaser,and Daniel K Sodickson. Generalized Bloch model: a theory for pulsed magnetization transfer. Magn Reson Med, 2021.
[13] J Assländer, MA Cloos, F Knoll, DK Sodickson, J Hennig, and R Lat-tanzi. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn Reson Med, 2018.
[14] Jonathan I. Tamir, Martin Uecker, Weitian Chen, Peng Lai, Marcus T.Alley, Shreyas S. Vasanawala, and Michael Lustig. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med., 2017.
[15] Debra McGivney, Anagha Deshmane, Yun Jiang, Dan Ma, Chaitra Badve, Andrew Sloan, Vikas Gulani, and Mark Griswold. Bayesian estimation of multicomponent relaxation parameters in magnetic resonance fingerprinting. Magn. Reson. Med., 2017
[16] J. Trzasko and A. Manduca. Local versus Global Low-Rank Promotionin Dynamic MRI Series Reconstruction. Proc Intl Soc Mag Reson Med, 2011.
[17] Xiaoxia Zhang, Quentin Duchemin, Kangning Liu, Sebastian Flassbeck, Cem Gultekin, Carlos Fernandez-Granda, and Jakob Assländer. Cramer-Rao bound-informed training of neural networks for quantitative MRI.page ArXiV ID: 2109.10535, 2021.
[18] Bruce Fischl, David H. Salat, André J.W. van der Kouwe, Nikos Makris,Florent Ségonne, Brian T. Quinn, and Anders M. Dale. Sequence-independent segmentation of magnetic resonance images. NeuroImage, 2004. Mathematics in Brain Imaging.
[19] Martin Reuter, H. Diana Rosas, and Bruce Fischl. Highly accurate inverse consistent registration: A robust approach. NeuroImage, 2010.
[20] Andrew Hoopes, Jocelyn S. Mora, Adrian V. Dalca, Bruce Fischl, and Malte Hoffmann. Synthstrip: skull-stripping for any brain image. NeuroImage, 2022.
Figures