1605
Mask-free T2* and R2* mapping with dual multi-dimensional integration (dMDI)
Yongquan Ye1, Jian Xu1, Zhongqi Zhang1, Yan Zhang2, Qiang Zhao3, Jiajia Xu3, and Huishu Yuan3
1United Imaging, Houston, TX, United States, 2Beijing United Imaging Intelligent Imaging Technology Research Institute, Beijing, China, 3Radiology, Peking University Third Hospital, Beijing, China
1United Imaging, Houston, TX, United States, 2Beijing United Imaging Intelligent Imaging Technology Research Institute, Beijing, China, 3Radiology, Peking University Third Hospital, Beijing, China
Synopsis
Keywords: Quantitative Imaging, Quantitative Imaging
A dual MDI strategy was developed and demonstrated to achieve T2* and R2* mapping that are both highly delineated between noise backgrounds and normal tissues as well as spikes free, thus eliminating the need for routine noise masking or manual segmentation.Introduction
Noise-mask has always been necessary in T2* (T2 as well) mapping to spiking results related to low signal-to-noise ratio(SNR) such as background noise, and to long T2* species like cerebral spinal fluids (CSF). The need for noise-masking has been essential to model-based curve fitting methods1, as well as non-model based analytical methods2,3, as they share two common aspects that are rarely discussed or conveniently ignored. The first one is that their T2* mapping results are non-specific between long T2* and low signal-to-noise ratio (SNR) signals, both of which create a ‘flat’ signal-time curve that will always be interpreted with long T2* values, because T2* cannot be 0 in the exponential model. The second is processing with real signals, which shows noise distribution of Rician or Rayleigh4 with non-zero means, rather than the zero-mean Gaussian. This noise distribution change will lead to strong T2* variations in the form of spikes for long T2*, low SNR and noise signals.Recently, a multi-dimensional integration (MDI) method5 was proposed to yield well-delineated T2* maps, generating high T2* for CSF but low T2* for noise background with minimal spikes. However, this only applied to T2*, not R2* maps. Nevertheless, the MDI method provided a potential perspective for T2* mapping via complex signal processing with Gaussian noise.
In this work, we propose a dual MDI strategy, namely dMDI, to achieve independent T2*/R2* mapping without the need for noise masking or manual extraction.
Methods
Denote the complex signal of the ith echo and jth coil channel as Si,j. According to the MDI theory5, a signal function GMDI is defined as the signal ratio between consecutive echoes:$$G_{MDI}(i,j)\equiv \left | \frac{S_{i+1,j}}{S_{i,j}} \right |= e^{-\frac{\Delta TE}{T_{2}^{*}}} [1]$$
And by solving $$$\min_{\Theta }\sum_{i}^{N_{e}-1}\sum_{j}^{N_{c}}\left \| S_{i+1,j}-S_{i,j}\cdot \Theta \right \|_{2}^{2}$$$, the numeric solution of GMDI can be efficiently calculated as:
$$\Theta _{MDI}=\left | \frac{\sum_{i}^{N_{e}-1}\sum_{j}^{N_{c}}S_{i,j}^{*}\cdot S_{i+1,j}}{\sum_{i}^{N_{e}-1}\sum_{j}^{N_{c}}\left | S_{i,j} \right |^{2}} \right | [2]$$
And the corresponding R2* and T2* values can be calculated as:
$$R_{2MDI}^{*}=-\frac{ln(\Theta _{MDI})}{\Delta TE} [3] $$
$$T_{2MDI}^{*}=-\frac{\Delta TE}{ln(\Theta _{MDI})} [4] $$
Eqs.1~4 are described previously5 and thus denoted with the subscript ‘MDI’. Similarly, an inversed signal function GMDIinv can be defined as:
$$G_{MDIinv}(i,j)\equiv \left | \frac{S_{i,j}}{S_{i+1,j}} \right |= e^{\frac{\Delta TE}{T_{2}^{*}}} [5]$$
And similarly:
$$\Theta _{MDIinv}=\left | \frac{\sum_{i}^{N_{e}-1}\sum_{j}^{N_{c}}S_{i+1,j}^{*}\cdot S_{i,j}}{\sum_{i}^{N_{e}-1}\sum_{j}^{N_{c}}\left | S_{i+1,j} \right |^{2}} \right | [6]$$
$$R_{2MDIinv}^{*}=\frac{ln(\Theta _{MDIinv})}{\Delta TE} [7] $$
$$T_{2MDIinv}^{*}=-\frac{\Delta TE}{ln(\Theta _{MDIinv})} [8] $$
Finally, the proposed dMDI strategy for T2*/R2* is:
$$R_{2dMDI}^{*}=\frac{-ln(\Theta _{MDI})+ln(\Theta _{MDIinv})}{2\Delta TE} [9] $$
$$T_{2dMDI}^{*}=\left [ \frac{\left | ln(\Theta _{MDI}) \right |+\left | ln(\Theta _{MDIinv}) \right |}{2\Delta TE} \right ]^{-1} [10] $$
Computer simulation and 3T (uMR Omega, United Imaging, Shanghai, China) multi-echo GRE knee data were used for demonstration. Non-linear Levenberg–Marquardt (NLM) curve fitting using the model $$$S(t)=be^{-a\cdot t}$$$, as well as the analytic NumART2 and ARLO3 methods, were adopted for comparison.
Results
The simulated Θs and ln(Θ) combinations as functions of SNR are shown in Figure 1. The signal ratios ΘMDI and ΘMDIinv approach their respective true values at sufficiently high SNR, but towards zero as SNR decreases (Fig.1a). Among the ln(Θ) combinations, the $$$[-ln(\Theta _{MDI})+ln(\Theta _{MDIinv})]/2$$$(in Fig.1b) and $$$[|ln(\Theta _{MDI})|+|ln(\Theta _{MDIinv})|]/2$$$ (Fig.1c) would also approach zero as SNR decreases. This means the corresponding T2* and R2* values of dMDI (Eqs.9&10) will both approach zero at low SNR, while achieving accurate results for decent SNR.Figure 2 shows T2*/R2* maps of the knee from different methods. Spikes and high-value backgrounds can be seen on the R2* map of MDI and the T2* maps of NLM, NumART and ARLO, but are totally eliminated in both maps of dMDI.
Figure 3 shows the direct overlaid images of T2* maps on the PD weighted anatomy magnitude image. The dMDI T2* of the cartilage and ligaments are well displayed with excellent structure details, while the NLM overlaid results display unreliable visual quality with numerous spikes and inconsistent backgrounds.
Discussion
The original MDI method has shown that, by jointly processing the complex signals from both signal dimensions of echoes and coil channels, the background T2* values can be suppressed due to the intrinsic cancellation of Gaussian noise. However, its R2* maps are still calculated as the reciprocal, thus yielding high R2* values where T2* is low. Therefore, noise masking is still needed for MDI R2* maps instead of T2* maps, merely flipping the situation of previous methods (Fig.2).On the other hand, by additionally constructing a directionally reversed MDI, i.e. the nominal reciprocal of MDI, opposite trends of SNR response in ln(Θ) can be achieved between MDI and MDIinv, especially in the low SNR regime. These opposite trends can negate each other when properly combined (Figs.1b&1c, Eqs.9&10), which is the working principle of dMDI to achieve intrinsic SNR dependency and spike elimination in both T2*/R2* maps. With virtually zero artifacts, the T2* maps can be directly overlaid onto the anatomic images without noise masking or manual segmentation, greatly improving the workflow and evaluation reliability (Fig.3).
Conclusion
In conclusion, a dMDI method was proposed and demonstrated. To the best of our knowledge, this is the first demonstration of both T2* and R2* mapping that simultaneously offer exceptional quality and accuracy and as a result, require noise masking for neither.Acknowledgements
No acknowledgement found.References
1. Cohen-Adad J. What can we learn from T2* maps of the cortex? NeuroImage 2014;93 Pt 2:189-200.
2. Hagberg GE, Indovina I, Sanes JN, Posse S. Real-time quantification of T(2)(*) changes using multiecho planar imaging and numerical methods. Magn Reson Med 2002;48(5):877-882.
3. Pei M, Nguyen TD, Thimmappa ND, et al. Algorithm for fast monoexponential fitting based on Auto-Regression on Linear Operations (ARLO) of data. Magn Reson Med 2015;73(2):843-850.
4. Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magn Reson Med 1995;34(6):910-914.
5. Ye Y, Lyu J, Sun W, et al. A multi-dimensional integration (MDI) strategy for MR T2 * mapping. NMR Biomed 2021;34(7):e4529.
Figures
Figure 1 a) Simulated MDI signal ratios ΘMDI and ΘMDIinv. b) shows the natural logarithm of the Θ curves and their direct- and absolute-averaged curves,
and c) shows the reciprocal curves of the ln(Θ) and their direct-
and absolute-averaged curves. The true values of ΘMDI and ΘMDIinv are 0.5 and 2.0, respectively.
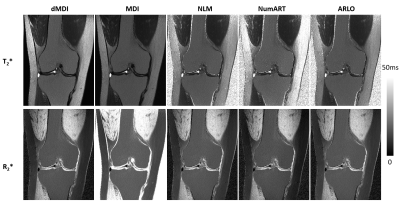
Figure 2 Comparison between T2* and R2* maps calculated with different methods. Note the backgrounds of each image, and that only dMDI has achieved background suppression and spike elimination in both maps.
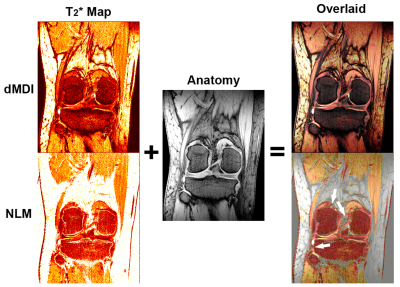
Figure 3 Illustration of the direct overlay of T2* maps onto the
anatomic magnitude images without the use of
any mask or segmentation on the T2*
maps. The display range of the T2* maps, by their own and in the
overlaid images, is all set to 0~50ms. The T2* maps are set with 50%
transparency in the overlaid images for optimal anatomy visualization. The very
high values in the NLM T2* maps appear transparent in its overlaid image were due to display settings, not masking. White
arrows indicate unreliable or indiscernible overlaying quality on cartilages or ligament.
DOI: https://doi.org/10.58530/2023/1605