Synopsis

Keywords: Machine Learning/Artificial Intelligence, Brain, Image Registration

Deep learning based affine registration is a fast and computationally efficient alternative to conventional iterative methods. However, existing solutions are not sensitive to local misalignments. We propose a non-rigid guided affine registration network with stochastic depth which was designed with an affine branch and an optional non-rigid branch. The probability of dropping the non-rigid branch was gradually increased over training epochs. During inference, the non-rigid branch was fully removed, thus making it a pure affine network guided by non-rigid transformations. Model training and quantitative evaluation was performed using a pre-registered multi-contrast brain MRI public dataset.

Introduction

Traditional iterative registration methods [1-4] are slow and cannot be easily implemented on hardware accelerators. Deep Learning (DL) based affine registration solutions [4] are a faster alternative but are not sensitive to local misalignments. Global affine alignments are mostly sufficient for non-deforming organs such as the brain, but are susceptible to local misalignments, especially when registering multi-contrast images. Designing a network to predict voxel-wise non-rigid parameters is too computationally expensive for the aforementioned applications. Therefore, we propose a hybrid approach through a novel affine registration DL network with stochastic depth. The stochastic depth comes from an optional branch that performs dense voxel-wise warping. The contribution of this branch is gradually decreased over training epochs, and at inference time we have a pure affine network but the predicted parameters were guided by the non-rigid branch.

Methods

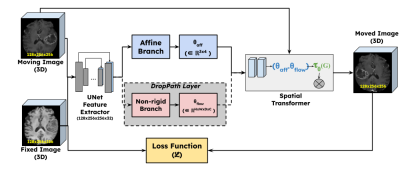
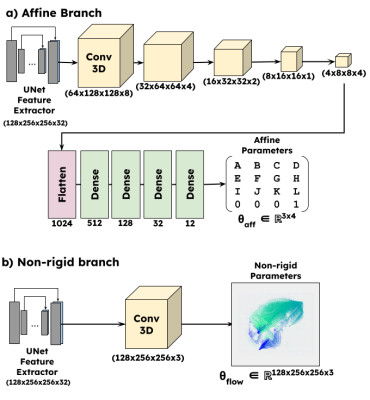
Network Design
Figure 1 shows the overall design of the proposed work. The premise of this work was based on an existing deformable registration framework Voxelmorph [6]. The input images (fixed and moving) were fed to a UNet style feature extractor. The network was then branched out into two parts: a) non-rigid branch, b) affine branch. The non-rigid branch is exactly the same as the Voxelmorph Dense network. The affine branch (Figure 2) was designed to downsample and flatten the feature space to predict an affine transformation matrix $$$\theta_{pred} \in \mathbb{R}^{n \times n+1}$$$ where $$$n$$$ is the dimensionality. The dense flow field and the affine parameters were concatenated and input as a composite transform to a differentiable spatial transformation layer [7]. The output of the spatial transformation layer (moved image) is subject to an objective function with respect to the fixed image.

Stochastic Depth and Probability Scheduling
The purpose of the non-rigid branch is purely to guide the affine transformation process. This is achieved by gradually reducing the contribution of the non-rigid branch over the training epochs. This was implemented as a DropPath layer [8] which is similar to Dropout, but it operates on a block of layers. The probability of the DropPath layer was gradually increased using a parameter scheduler. For the first few epochs, the non-rigid branch was always used; after this, for every epoch the probability was increased approximately by 5%. By the end of model training and during inference, the non-rigid branch was completely ignored. When the non-rigid branch was dropped, the corresponding input to the composite transformation was an identity transformation.

Dataset
We used the BraTS 2021 public dataset [9-11] having 1251 cases of T1, T1-CE, T2 and FLAIR images, along with ground truth tumor segmentations. 1126 cases of T1 and T1CE images, were used for training and 125 for validation and quantitative evaluation.

Training Pair Generation
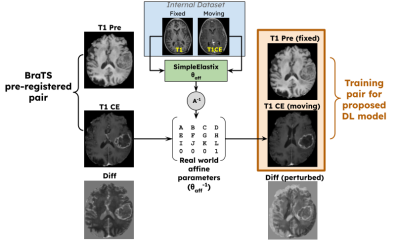
As the BraTS dataset was pre-registered, the perturbations had to be simulated. The training pair generation scheme is similar to [4], except that, instead of randomly generating affine transformations, they were extracted from a real-world multi-contrast internal dataset. As shown in Figure 3, the T1 and T1CE volumes from the internal dataset were affine registered using SimpleElastix[12], and the inverse of the affine matrix $$$\theta_{sim}$$$ was randomly applied on the BraTS dataset. This helped the BraTS dataset to have realistic perturbations. The ground truth tumor masks $$$M$$$ were also perturbed for quantitative using $$$\theta_{sim}$$$ and are referred to as $$$M_{sim}$$$.

Experiments
Two models were trained in addition to the proposed model, in order to perform a comparative analysis. The first model was trained using only the affine branch in the training phase while the second model was a recursive cascaded network proposed in [13]. All three models were trained with a weighted combination of normalized mutual information (NMI)[14], normalized cross-correlation (NCC)[15] and mean squared error (MSE) losses.

Quantitative Evaluation
All the models were quantitatively evaluated using MSE, structural similarity index metric (SSIM) and peak signal-to-noise ratio (PSNR) as described in [4]. The MSE was computed between the SimpleElastix predicted $$$(\theta_{sim})^{-1}$$$ and $$$\theta_{pred}$$$, while the PSNR and SSIM were computed between the images registered by the different models and the pre-registered images available in the BraTS dataset. Dice scores were computed as $$$Dice(M, \hat{M})$$$ where $$$\hat{M} = M_{sim} . \theta_{pred}$$$

Results

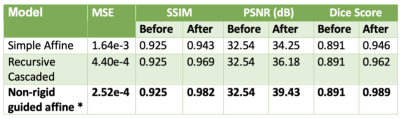
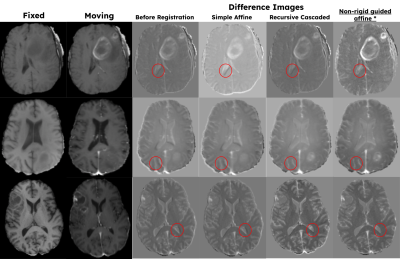
Figure 4 tabulates the quantitative metrics of the different models and shows that the proposed model performs the best. Figure 5 shows some qualitative examples on the validation cases. The highlighted areas in Figure 5 show that the proposed model is sensitive to local misalignments.

Discussions

Quantitative and qualitative assessments show that the proposed model performs better than the other competitive models for accurate affine registration of brain MRI images. The results also show that the proposed model is sensitive to local misalignments whereas conventional DL-based affine models are not. The same scheme can be extended to register multi-contrast MRI images (T2 and FLAIR) and cross-modal volumes (PET/CT or PET/MR). When applicable, the non-rigid path can be partially enabled during inference time to model non-rigid deformations.

Conclusion

We have proposed a unique DL network for affine registration where the parameters are guided by an optional non-rigid network branch.

Acknowledgements

We would like to acknowledge the grant support of NIH R44EB027560.