1375
Improved Bayesian Brain MR Image Segmentation by Incorporating Subspace-Based Spatial Prior into Deep Neural Networks
Yunpeng Zhang1, Huixiang Zhuang1, Ziyu Meng1, Ruihao Liu1,2, Wen Jin2,3, Wenli Li1, Zhi-Pei Liang2,3, and Yao Li1
1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States
1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Segmentation
Accurate segmentation of brain tissues is important for brain imaging applications. Learning the high-dimensional spatial-intensity distributions of brain tissues is challenging for classical Bayesian classification and deep learning-based methods. This paper presents a new method that synergistically integrate a tissue spatial prior in the form of a mixture-of-eigenmodes with deep learning-based classification. Leveraging the spatial prior, a Bayesian classifier and a cluster of patch-based position-dependent neural networks were built to capture global and local spatial-intensity distributions, respectively. By combining the spatial prior, Bayesian classifier, and the proposed networks, our method significantly improved the segmentation performance compared with the state-of-the-art methods.Introduction
Accurate segmentation of brain MR images is important for assessment of brain development, aging, and various brain disorders. Although varieties of methods have been developed, including Bayesian classification-based methods1-4 and deep learning-based methods5-8, segmentation accuracy needs further improvement for general practical applications. A fundamental challenge is the learning of the underlying high-dimensional spatial-intensity distributions of brain tissues. Classical mixture of Gaussian (MOG) modeling of intensity distribution of brain tissues could not effectively capture the spatial information and showed poor performance in segmenting subtle image details. Deep learning-based methods have shown good potential to capture the spatial-intensity distribution but require large amounts of training data to avoid the overfitting problem. In this study, we proposed a new Bayesian segmentation method by incorporating a subspace-based spatial prior in the form of a mixture-of-eigenmodes into deep learning-based classification to effectively capture the spatial-intensity distribution of brain tissues. The proposed method achieved significantly improved segmentation performance across multiple public datasets and images with distortions, in comparison with the state-of-the-art methods.Methods
The proposed method effectively captures the spatial-intensity distribution of brain tissues by integrating subspace-based modeling to capture global spatial distribution and deep neural network for local spatial-intensity distribution learning. The overall pipeline of the methodology is shown in Fig. 1, which contains four integral components: 1) a subspace model to capture the spatial prior of brain tissues, 2) a Bayesian classifier to capture the global spatial-intensity distribution, 3) a position-dependent patch-based neural network (PDNN) to capture the local spatial-intensity distribution, and 4) a fusion network that integrates above three components for final decision.Subspace model of spatial-intensity distribution of brain tissues
The probability of observing tissue label $$${k}$$$ at voxel $$${i}$$$ is denoted as $$${p}({x}_{i}={k})={\pi}_{k}({x}_{i})$$$, where $$${i}{\in}\{1,2,...,{d}\}$$$. For each tissue class $$${k}{\in}\{1,2,...,{K}\}$$$, we represent the spatial distribution $$${\pi}_{k}$$$ using a low-dimensional subspace model as: $${\pi}_{k}({x}_{1},{x}_{2},...,{x}_{d}){\approx}{\sum}_{r=1}^R{\alpha}_{r,k}{\phi}_{r,k}(\boldsymbol{x})$$ where $$$\{{\phi}_{r,k}(\boldsymbol{x})\}$$$ are the spatial-population basis functions (or eigen modes) obtained by applying principal component analysis to the tissue probability maps $$$\{{\pi}_{k}(\boldsymbol{x})\}$$$ over the training images, and $$$\{{\alpha}_{r,k}\}$$$ are the subspace probability model coefficients. Given that $$$\sum_{k=1}^{K}{\pi}_{k}({x}_{i})={1}$$$ for all $$${i}$$$, the normalized prior tissue probability map $$$\{{\hat \pi}_{k}(\boldsymbol{x})\}$$$ can be obtained as: $${\hat \pi}_{k}({x}_{i})=\frac{\sum_{r=1}^{R}{\alpha}_{r,k}{\phi}_{r,k}({x}_{i})}{\sum_{j=1}^{K}\sum_{r=1}^{R}{\alpha}_{r,j}{\phi}_{r,j}({x}_{i})}$$
Bayesian classifier
Given the subspace-based spatial prior, a Bayesian classifier is built to capture the global spatial-intensity distribution. Specifically, the likelihood function is modeled by MOG: $${p}({y}_{i}|{x}_{i}={k},{\boldsymbol \mu}_{k},{\boldsymbol \sigma}_{k},{\boldsymbol \lambda}_{k}) = \sum_{m=1}^{{M}_{k}}\frac{{\lambda}_{k_m}}{\sqrt{2{\pi}{\sigma}_{k_m}^2}}\text{exp}(-\frac{({y}_{i}-{\mu}_{k_m})^2}{2{\sigma}_{k_m}^2})$$ where $$${y_i}$$$ and $$${x_i}$$$ represent the image intensity and tissue label at $$${i}$$$-th voxel, and $$$\{{\boldsymbol \mu}_{k},{\boldsymbol \sigma}_{k},{\boldsymbol \lambda}_{k})\}$$$ are the model parameters estimated from training data using the Levenberg-Marquardt algorithm. Leveraging the likelihood function and subspace-based spatial prior, a Bayesian classifier is built using Maximum-A-Posteriori estimation.
PDNN classifier
To capture the local joint spatial-intensity distributions, a cluster of PDNNs were trained to model $$$p({x}_{i}|{\boldsymbol{y}}_{{\boldsymbol{s}}_{i}})$$$, where $$${\boldsymbol{y}}_{{\boldsymbol{s}}_{i}}$$$ is the sub-volume centered at the $$${i}$$$ -th voxel. Here $$${p}({x}_{i}|{\boldsymbol{y}}_{{\boldsymbol{s}}_{i}})$$$ serves as an approximation of $$${p}({x}_{i}|{\boldsymbol y})$$$. This cluster of PDNNs could be viewed as a generalization of the classical Markov random field model without spatial stationarity and Gaussianity. Specifically, the prior spatial probability of each voxel obtained from previous step could be quantized into $$${L}$$$ levels. The collection of voxels with the same quantized probability are assumed to have the same spatial-intensity distribution and modeled by a single network. The parameters of each network $$$f({\boldsymbol y}_{{\boldsymbol s}_{i}};{\boldsymbol \theta})$$$ was optimized by minimizing the cross-entropy loss based on the training data pair $$$\{{\boldsymbol y}_{{\boldsymbol{s}}_{{m}_{l}}},{b}_{m_{l}}\}$$$ selected for the corresponding probability level: $$\mathop{min}\limits_{\boldsymbol\theta}\{-\frac{1}{M}\sum_{m=1}^{M}{b}_{m_{l}}\text{log}(f({\boldsymbol{y}}_{{\boldsymbol{s}}_{m}};{\boldsymbol\theta}))+(1-{b}_{{m}_{l}})\text{log}(1-f({\boldsymbol{y}}_{{\boldsymbol{s}}_{m}};{\boldsymbol\theta}))\}$$
where $$$b_{m_l}$$$ denotes the real tissue label of the $$${m}$$$-th voxel at the $$${l}$$$-th level. In this way, the spatial heterogeneity of local spatial-intensity distribution is well learned.
Fusion network
The final classification is determined by fusing the subspace-based spatial prior, Bayesian classification and PDNN classification using a 3D UNet-based fusion network.
Results
The performance of the proposed method was compared with 3D-UNet and VoxResNet7. To obtain the spatial prior, we used 2819 T1w brain MR images, including HCP9 (N = 1000), ADNI10 (N = 1269), and CamCAN11 (N = 550) datasets. For network training, we used the labeled data from MALC 2012 challenge. The performance of our proposed method was evaluated on MALC 2012 challenge data and HCP T1w images, respectively. As can be seen from the results in Fig. 2, our proposed method achieved the best results in both MALC 2012 challenge and HCP datasets. We also investigated the performance of our method in images with motion artifacts and field inhomogeneity distortions. As shown in Fig. 3, our proposed method outperformed other deep learning-based methods in both cases. Figure 4 shows the advantage of using our proposed subspace-based prior compared to the traditional SPM prior. Quantitative analysis also indicates that the proposed method had improved performance compared with the state-of-the-art methods, as shown in Table 1.Conclusions
This paper presents a new method for improved brain tissue segmentation by incorporating subspace-based spatial prior into deep learning-based Bayesian classification. The proposed method showed significantly improved accuracy and robustness across multiple public brain MR image datasets in comparison with the state-of-the-art methods. With further development, the method may provide a useful tool for accurate segmentation of brain tissues for brain image processing applications.Acknowledgements
This work was supported by Shanghai Pilot Program for Basic Research—Shanghai Jiao Tong University (21TQ1400203); the National Natural Science Foundation of China (81871083); and Key Program of Multidisciplinary Cross Research Foundation of Shanghai Jiao Tong University (YG2021ZD28).References
- Ashburner J, Friston KJ. Unified segmentation. Neuroimage, 2005; 26(3), 839-851.
- Fischl Bruce, et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002; 33(3): 341-355.
- Zhang Y, Brady M, and Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001; 20(1): 45-57.
- Tu Z, Narr KL, Dollár P, et al. Toga AW. Brain anatomical structure segmentation by hybrid discriminative/generative models. IEEE Trans Med Imaging. 2008; 27(4): 495-508.
- Sun L, Ma W, Ding X, Huang Y, et al. A 3D spatially weighted network for segmentation of brain tissue from MRI. IEEE Trans Med Imaging, 2019; 39(4): 898-909.
- Moeskops P, Viergever MA, Mendrik AM, et al. Automatic segmentation of MR brain images with a convolutional neural network. IEEE Trans Med Imaging. 2016; 35(5): 1252-1261.
- Chen H, Dou Q, Yu L, Qin J, et al. VoxResNet: Deep voxel-wise residual networks for brain segmentation from 3D MR images. NeuroImage. 2018; 170:446-55.
- Sun L, Shao W, Zhang D, et al. Anatomical attention guided deep networks for ROI segmentation of brain MR images. IEEE Trans Med Imaging, 2019; 39(6):2000-12.
- Van Essen DC, Smith SM, Barch DM, et al. The WU-Minn human connectome project: an overview. Neuroimage. 2013; 80:62-79.
- Jack Jr CR, Bernstein MA, Fox NC, et al. The Alzheimer's disease neuroimaging initiative (ADNI): MRI methods. J Magn Reson. 2008;27(4):685-91.
- Taylor, J.R., et al., The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. Neuroimage, 2017; 144: 262-269.
Figures
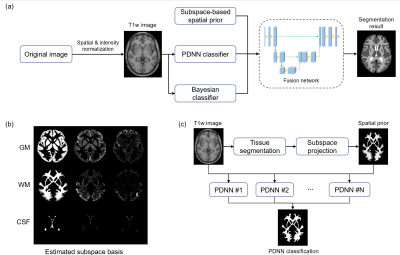
Figure 1. Illustration of the proposed segmentation framework. (a)
Overall pipeline of the method. (b) Estimated spatial subspace basis. (c) Pipeline
of the position-dependent neural network (PDNN) classifier.
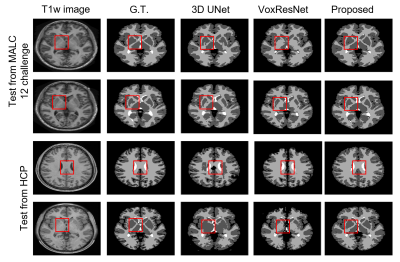
Figure 2.
Tissue segmentation results on MALC 12 challenge and HCP data. For in-site MALC 12 challenge
data, the proposed method achieved the best performance in the regions with
ambiguity in image intensity, e.g., the deep gray matter area. For out-of-site HCP
data, the proposed method showed robust segmentation performance, while both 3D
UNet and VoxResNet showed obvious segmentation errors.
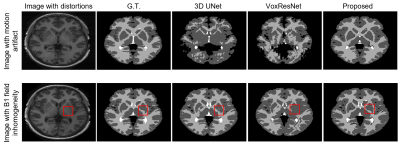
Figure 3.
Tissue segmentation results on images with simulated motion artifacts and B1 field inhomogeneity distortions.
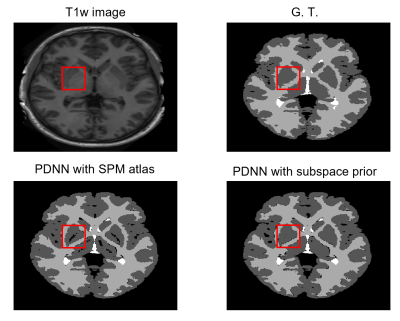
Figure 4. Comparison
of segmentation performance using the statistical atlas from SPM toolbox and
our proposed subspace-based prior.
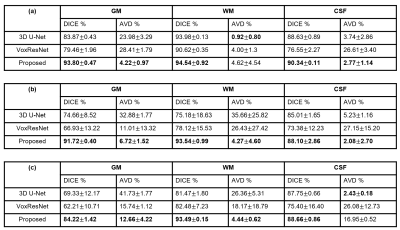
Table 1. Comparison
of segmentation performance on (a) MALC 12 challenge data, (b) T1w images with
motion artifacts, and (c) HCP T1w images. Our proposed method shows the best
accuracy in all three cases.
DOI: https://doi.org/10.58530/2023/1375