1363

Disentangling T1 relaxation from MT effects in the MP2RAGE sequence
Lucas Soustelle1,2, Andreea Hertanu1,2, Thomas Troalen3, Maxime Guye1,2, Jean-Philippe Ranjeva1,2, Guillaume Duhamel1,2, and Olivier M. Girard1,2
1Aix-Marseille Univ, CNRS, CRMBM, Marseille, France, 2APHM, Hôpital Universitaire Timone, CEMEREM, Marseille, France, 3Siemens Healthcare SAS, Marseille, France

Synopsis

Keywords: Relaxometry, Modelling, Microstructure, Nervous System

Common T1 mapping methods are dependent on the biophysical model assumptions. Previous work based on a qMT-SPGR framework demonstrated the influence of magnetization transfer effects and the importance of appropriate sequence design and signal modelling for T1 estimation. In this work, we expanded upon this optimized framework using an MP2RAGE sequence and demonstrated that quantitative T1 values in agreement with VFA-based experiments can be obtained in the human brain.

Introduction

Brain in vivo mapping of the longitudinal relaxation time (T1) has demonstrated interest in neuroimaging due to its quantitative feature and sensitivity to microstructure1–3. Three techniques have been commonly used, namely the Variable Flip Angle (VFA)4, Look-Locker5 and inversion-recovery spin-echo6 (IR-SE; historically referred to as the gold-standard). Nowadays, the Magnetization Prepared 2 RApid Gradient Echo (MP2RAGE)7 sequence becomes widely used thanks to its reproducibility8,9 and beneficial trade-offs between spatial coverage, acquisition time, resolution and signal-to-noise ratio.

Although the MP2RAGE sequence was validated against the IR-SE method7,10 on aqueous phantoms (i.e., without magnetization transfer [MT] effects), theory and observations indicate that MT effects occur in biological tissues, hence invalidating the classical single-pool models6,7. The resulting multi-exponential relaxation11–14 makes usual T1 estimations dependent on the respective acquisition parameters.

To address this issue, a recently optimized framework combining appropriate sequence design and signal modelling accounting for MT effects in SPGR-VFA data was used to remove biases on the free pool T1 (T1,f) estimator15. In this work, we propose to adapt this framework to the MP2RAGE sequence and compare the estimated T1,f values with those obtained with the VFA sequence.

Methods

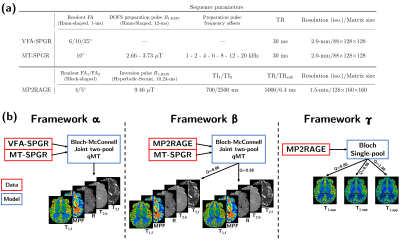
Experiments were performed on three healthy volunteers on a 3T clinical system (MAGNETOM Vida, Siemens Healthineers, Erlangen, Germany) with body coil transmission and a 32-channel receive head coil. The protocol included anatomical MPRAGE, B1+ mapping, the constructor 3D-MP2RAGE and prototype 3D non-selective VFA-SPGR and MT-SPGR sequences. Optimized dual-offset saturation pulses were used for Z-spectra MT-SPGR acquisitions15. A summary of the sequence parameters is provided in Figure 1a.

As in Ref.15, the two-pool model was adapted into general matrix equations16 accounting for any on/off-resonance saturation, relaxation and exchanges, and allows for a joint fitting of MT-SPGR and VFA-SPGR data (framework α). The MP2RAGE-UNI data were modelled in a similar fashion for a joint fitting with MT-SPGR data (framework β). Finally, the classical single-pool model introduced by Marques et al.7 was used to derive apparent T1 (T1,app) maps (framework γ). All frameworks included B1+ correction regarding the flip angles and saturation terms. For framework β, the inversion efficiency (Q) of the MP2RAGE’s inversion pulse was set to mean values previously estimated in white matter (WM) and grey matter (GM)17, i.e. Q=0.86/0.88, respectively; these values are consistent with Bloch simulations of the employed hyperbolic-secant inversion pulse (Q=0.87 for a single-pool T1/T2=50/1000 ms and on resonance; not shown). For framework γ, Q was set to 0.86, 0.967,18 and 1.00. Quantitative MT parameters of bound (b) and free (f) pools T2,f, T2,b, T1,f (assuming T1,b=T1,f), macromolecular proton fraction (MPF) and exchange rate R were estimated for frameworks α and β. A description of the different frameworks is provided in Figure 1b.

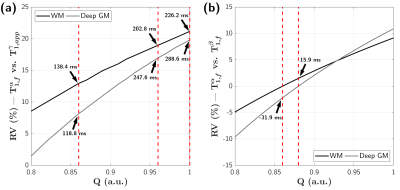
The biases of all quantitative parameters in frameworks β and γ were simulated as a function of Q by fitting synthetic MP2RAGE-UNI signals accounting for MT effects and based on qMT parameters of GM and WM estimated by framework α and for fixed Q spanning from 0.80 to 1.00. Relative variations (RV(Q)=(T1,fα-T1,estβ/γ(Q))/T1,fα) were then calculated.

Quantitative parameters were evaluated in WM and deep GM regions of interest (ROI), respectively retrieved from the JHU probabilistic atlas19 using ANTs20 and FreeSurfer21. Bland-Altman analyses were performed.

Results

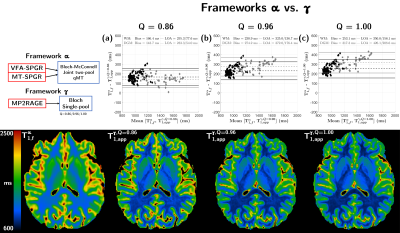
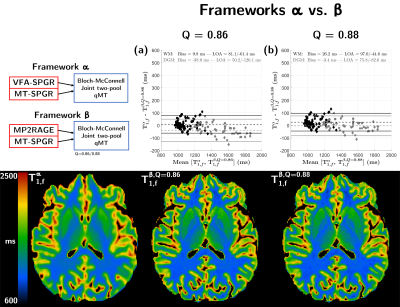
Figure 2a shows simulation results indicating an increasing underestimation of T1,f in framework γ compared to framework α as Q increases, yielding ΔT1=T1,fα-T1,appγ of 138.4/202.8/226.2 ms in WM and 118.8/247.6/288.6 ms in GM for Q=0.86, 0.88 and 1.00, respectively. These results are consistent with the experimental biases found in Bland-Altman analyses (Figure 3a-c; ΔT1=166.4/230.9/253.1 ms in WM, and ΔT1=143.7/274.2/317.3 ms in GM for Q=0.86/0.96/1.00). Representative axial views of T1,fα and T1,appγ maps are provided in Figure 3.

Figure 2b presents simulation results comparing frameworks α and β, and indicates an increasing trend of RV as a function of Q. Low T1,f biases were found, with ΔT1=‑31.9 ms in GM at Q=0.86 and ΔT1=15.9 ms in WM at Q=0.88. Experimental results (Figure 4a-b) are again consistent with simulations, with low ΔT1=9.8 ms in WM for Q=0.86 and mild ΔT1=-38.0 ms in GM. Conversely for Q=0.88, ΔT1 becomes very low in GM (ΔT1=-3.4 ms) while increasing for WM (ΔT1=26.2 ms). Representative axial views of T1,fα and T1,fβ maps are provided in Figure 4.

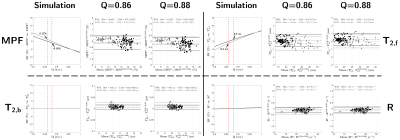
Comparison of other qMT parameters between frameworks α and β are provided in Figure 5, with close-to-zero values at both Q=0.86/0.88 for T2,f, T2,b and R. MPF shares the same trend as T1,f (Figure 4), presumably due to the inter-parameter correlation22. Overall, experimental results are still in accordance with simulations (Figure 5).

Discussion and conclusion

We demonstrated that accounting for MT effects by adapting the signal model dramatically reduces the bias on the estimated T1 from combined MP2RAGE and MT-SPGR data, yielding T1 and qMT parameters close to those estimated with the VFA-qMT method (framework α). The resulting T1 nonetheless depends on pre-set Q values, highlighting the interest of either disposing of an external Q map or to estimate Q as it is performed by the MP3RAGE method17. Overall, our results indicate that MP2RAGE-T1 can be disentangled from MT effects, hence holding promises for reproducible quantitative MRI protocols independent from sequence parameters.

Acknowledgements

This work was supported by the French National Research Agency ANR [ANR‐22‐CE17‐0041] and ARSEP 2020.

References

1. Does MD. Inferring brain tissue composition and microstructure via MR relaxometry. Neuroimage. 2018;(October 2017):1-13. doi:10.1016/j.neuroimage.2017.12.087

2. Margaret Cheng H-L, Stikov N, Ghugre NR, Wright GA. Practical medical applications of quantitative MR relaxometry. J Magn Reson Imaging. 2012;36(4):805-824. doi:10.1002/jmri.23718

3. Harkins KD, Xu J, Dula AN, et al. The microstructural correlates of T1 in white matter. Magn Reson Med. 2015;00(February):n/a-n/a. doi:10.1002/mrm.25709

4. Fram EK, Herfkens RJ, Johnson GA, et al. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magn Reson Imaging. 1987;5(3):201-208. doi:10.1016/0730-725X(87)90021-X

5. Look DC, Locker DR. Time Saving in Measurement of NMR and EPR Relaxation Times. Rev Sci Instrum. 1970;41(2):250-251. doi:10.1063/1.1684482

6. Hahn EL. An Accurate Nuclear Magnetic Resonance Method for Measuring Spin-Lattice Relaxation Times. Phys Rev. 1949;76(1):145-146. doi:10.1103/PhysRev.76.145

7. Marques JP, Kober T, Krueger G, van der Zwaag W, Van de Moortele P-F, Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage. 2010;49(2):1271-1281. doi:10.1016/j.neuroimage.2009.10.002

8. Mussard E, Hilbert T, Forman C, Meuli R, Thiran J, Kober T. Accelerated MP2RAGE imaging using Cartesian phyllotaxis readout and compressed sensing reconstruction. Magn Reson Med. 2020;84(4):1881-1894. doi:10.1002/mrm.28244

9. Hilbert T, Soustelle L, Piredda GF, et al. On Comparability and Reproducibility of Myelin Sensitive Imaging Techniques. In: Proceedings 30th Scientific Meeting, International Society for Magnetic Resonance in Medicine. Online; 2021.

10. Rasoanandrianina H, Massire A, Taso M, et al. Regional T 1 mapping of the whole cervical spinal cord using an optimized MP2RAGE sequence. NMR Biomed. 2019;32(11):1-17. doi:10.1002/nbm.4142

11. Dortch RD, Li K, Gochberg DF, et al. Quantitative magnetization transfer imaging in human brain at 3 T via selective inversion recovery. Magn Reson Med. 2011;66(5):1346-1352. doi:10.1002/mrm.22928

12. Dortch RD, Moore J, Li K, et al. Quantitative magnetization transfer imaging of human brain at 7T. Neuroimage. 2013;64(1):640-649. doi:10.1016/j.neuroimage.2012.08.047

13. van Gelderen P, Jiang X, Duyn JH. Effects of magnetization transfer on T 1 contrast in human brain white matter. Neuroimage. 2016;128:85-95. doi:10.1016/j.neuroimage.2015.12.032

14. Manning AP, MacKay AL, Michal CA. Understanding aqueous and non-aqueous proton T1 relaxation in brain. J Magn Reson. 2021;323:106909. doi:10.1016/j.jmr.2020.106909

15. Soustelle L, Troalen T, Hertanu A, et al. Quantitative Magnetization Transfer parametric mapping unbiased by on-resonance saturation and dipolar order contributions. In: Proceedings of the 31st Annual Meeting of ISMRM. London; 2022:2709.

16. Malik SJ, Teixeira RPAG, West DJ, Wood TC, Hajnal J V. Steady‐state imaging with inhomogeneous magnetization transfer contrast using multiband radiofrequency pulses. Magn Reson Med. 2020;83(3):935-949. doi:10.1002/mrm.27984

17. Olsson H, Andersen M, Kadhim M, Helms G. MP3RAGE: Simultaneous mapping of T 1 and B1+ in human brain at 7T. Magn Reson Med. 2022;87(6):2637-2649. doi:10.1002/mrm.29151

18. O’Brien KR, Magill AW, Delacoste J, et al. Dielectric pads and low- B1+ adiabatic pulses: Complementary techniques to optimize structural T 1 w whole-brain MP2RAGE scans at 7 tesla. J Magn Reson Imaging. 2014;40(4):804-812. doi:10.1002/jmri.24435

19. Wakana S, Caprihan A, Panzenboeck MM, et al. Reproducibility of quantitative tractography methods applied to cerebral white matter. Neuroimage. 2007;36(3):630-644. doi:10.1016/j.neuroimage.2007.02.049

20. Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. Neuroimage. 2011;54(3):2033-2044. doi:10.1016/j.neuroimage.2010.09.025

21. Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis. Neuroimage. 1999;9(2):179-194. doi:10.1006/nimg.1998.0395

22. Yarnykh VL, Bowen JD, Samsonov A, et al. Fast Whole-Brain Three-dimensional Macromolecular Proton Fraction Mapping in Multiple Sclerosis. Radiology. 2015;274(1):210-220. doi:10.1148/radiol.14140528


Figures

Figure 1: Summary of SPGR and MP2RAGE sequence parameters (a) and description of frameworks α, β and γ (b). MT-SPGR sequences were prepared using symmetric and simultaneous dual offset frequency saturation (DOFS) pulses, as described in Ref. 15. TRsub in the MP2RAGE refers to the inter-echo time in the RAGE modules.

Figure 2: Simulation of the relative variations of T1,fα vs. T1,appγ (a) and T1,fα vs. T1,fβ (b). The synthetic UNI signal of the MP2RAGE sequence was generated using representative qMT parameters as estimated experimentally with framework α (WM: T1,f=1069.8 ms, T2,b=10.4 µs, R=22.8 s-1, T2,f=18.9 ms, MPF=15.5%; deep GM: T1,f=1458.3 ms, T2,b=10.0 µs, R=22.9 s-1, T2,f=29.4 ms, MPF=9.4%). ΔT1=T1,fα- T1,estβ/γ values are reported for remarkable Q values depicted by the consecutive red dashed vertical lines (Q=0.86/0.96/1.00 for (a) and Q=0.86/0.88 for (b)).

Figure 3: Bland-Altman plots of T1 values in WM and deep GM ROIs comparing frameworks α and γ for estimation at Q=0.86 (a), Q=0.96 (b) and Q=1.00 (c). Biases and limits of agreements (LOA) are respectively indicated in dashed and solid lines. Each subject is depicted by a different symbol (circle, diamond and square). Representative axial views T1,fα and T1,appγ are also shown (bottom).

Figure 4: Bland-Altman plots of T1 values in WM and deep GM ROIs comparing frameworks α and β for estimation at Q=0.86 (a) and Q=0.88 (b). Biases and limits of agreements (LOA) are respectively indicated in dashed and solid lines. Each subject is depicted by a different symbol (circle, diamond and square). Representative axial views T1,fα and T1,fβ are also shown (bottom).

Figure 5: Simulation of the relative variations and Bland-Altman plots from WM and deep GM ROIs comparing frameworks α and β for Q=0.86 and Q=0.88 for MPF (top left), T2,f (top right), T2,b (bottom left) and R (bottom right). The synthetic MP2RAGE-UNI signal was generated using representative qMT parameters estimated with framework α. Biases and limits of agreements (LOA) are respectively indicated in dashed and solid lines. ΔMPF=MPFα-MPFβ and ΔT2,f=T2,fα-T2,fβ values are reported for remarkable Q values depicted by the consecutive red dashed vertical lines Q=0.86/0.88.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
1363
DOI: https://doi.org/10.58530/2023/1363