Synopsis

Keywords: Relaxometry, Data Analysis, phase-cycled bSSFP, T1-quantification, T2-quantification, B0 quantification, proton-density quantification, multi-parameter quantification

A novel analytical method for off-resonance encoded parameter quantification of voxel-wise phase-cycled bSSFP signal profiles was developed. The approach conserves both magnitude and phase information in a complete, linearized, and compact way. A framework for ultra-rapid and simultaneous $$$T_1$$$, $$$T_2$$$, $$$B_0$$$ inhomogeneity and proton density quantification were developed. The approach was validated in simulations, phantom and in vivo knee experiments and compared with gold-standard reference measurements when available. Simulations and experiments validated the proposed method for multi-parameter quantification with high accuracy and precision, providing the first step towards novel analytical quantification possibilities with phase-cycled bSSFP.

Introduction

Phase-cycled (PC) balanced steady-state free-precession (bSSFP) acquisitions enable a simultaneous quantification of $$$T_1$$$ and $$$T_2$$$ [1,2]. In prior methods, off-resonance effects were corrected after dismissing valuable parts of the phase information [1,2,3], requiring lengthy iterative processes to retrieve the underlying quantitative information.
This study aims to develop an Off-Resonant encoded Analytical parameter quantification using Complex Linearized Equations (ORACLE) from PC-bSSFP signal-profiles. We demonstrate that by using the entirety of encoded information, $$$T_1$$$, $$$T_2$$$, proton-density (PD) and magnetic field inhomogeneity ($$$B_0$$$) quantification of single-compartment systems is possible, and a clear visual separation of tissues by chemical-shift.

Methods

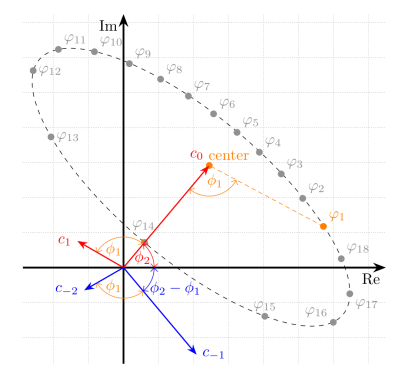
PC-bSSFP Fourier-space
PC-bSSFP equations have been represented in spatial magnetization-space [1,4]. For independent $$$T_1$$$ and $$$T_2$$$ quantification it is required to use complex data i.e., independent $$$M_x$$$ and $$$M_y$$$ information. Since the signal-evolution along the PC-dimension is exhibiting $$$\text{mod}(2\pi)$$$-ambiguities and non-linear dynamics due to off-resonance effects, information is challenging to extract. This problem is simplified by transforming the signal $$$S(\varphi)$$$ into Fourier-space [2,3]:
$$c_n=\sum_{j=0}^{N-1}S(\varphi_j)\cdot \text{e}^{\text{i}\,n\,\varphi_j}\, , \quad \varphi_j = \frac{2\,\pi}{N}\cdot j\,,\quad j =[0,N-1]\; ,$$
where $$$N$$$ is the number of phase-cycles, $$$c_n$$$ the $$$\text{n}^\text{th}$$$-mode, and $$$\varphi$$$ the RF-pulse phase-cycle increment. Discrete Fourier-transformation has three mathematical advantages: First, it generates a new complex space that provides a phase-quantification without $$$\text{mod}(2\pi)$$$-ambiguity. Second, it handles off-resonance effects as constant linear phase-factors, linearizing the problem. Finally, it compresses almost all information in the center of the Fourier-mode-space, summarizing the entire system in three modes $$$c_{-1}$$$, $$$c_0$$$ and $$$c_1$$$ similar to the relation between k-space and image-space (Figure 1). These three central modes form the basis of our proposed approach and are an irreducible and complete representation of the system, comprising $$$T_1$$$, $$$T_2$$$, PD and $$$B_0$$$-inhomogeneity.
Simulations and Experiments
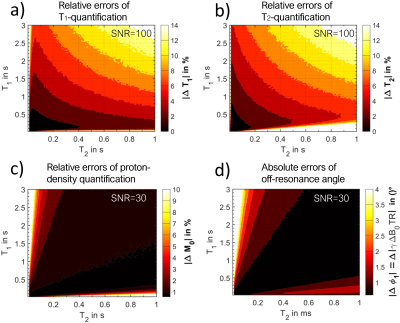
Simulations: The accuracy and precision of multi-parameter quantification is dependent on ($$$T_1$$$,$$$T_2$$$)-value-pairs and SNR. To investigate the quantification-error of $$$T_1$$$, $$$T_2$$$, $$$\Delta B_0$$$ and PD values, Monte-Carlo-simulations of the Bloch-equations for PC-bSSFP (5000 for each ($$$T_1$$$,$$$T_2$$$)-value-pair) with an SNR of 100 for $$$T_1$$$ and $$$T_2$$$ and 30 for $$$\Delta B_0$$$ and PD quantification were performed, while varying $$$T_1$$$ and $$$T_2$$$. The latter SNR was chosen, to demonstrate the high robustness of parameter quantification with ORACLE. $$$N=18$$$, $$$\alpha=15^\circ$$$, and $$$\text{TR}=5\,\text{ms}$$$ were used to be sensitive to biological plausible $$$T_1<1500\,\text{ms}$$$ and $$$T_2<400\,\text{ms}$$$ values. Next, the obtained profiles were processed with ORACLE and the root-mean-square-error of $$$T_1$$$, $$$T_2$$$, $$$\Delta B_0$$$ and PD was determined and plotted as function of $$$T_1$$$ and $$$T_2$$$.
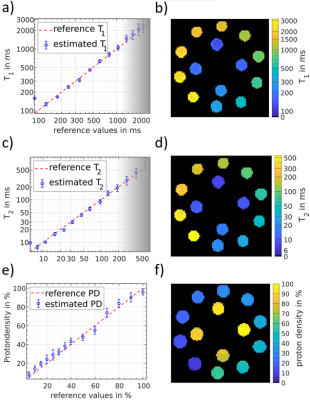
Phantom-experiments: 3 separate PC-bSSFP experiments on a standardized NIST-phantom [5] were performed at 3T (PRISMA, Siemens Healthineers). Scan parameters were equal to simulation parameters, with FOV of (223x223x202)mm with (1.4mm)³ isotropic resolution and BW=975kHz. To obtain a reference for $$$\Delta B_0$$$-mapping and to check for B0-drift, multi-echo-gradient-echo (ME-GRE) acquisitions were performed before each PC-bSSFP-acquisition and after the last PC-bSSFP-acquisition, resulting in four ME-GRE scans in total. For $$$B_1$$$-correction GRE-acquisitions were performed using the double-flip-angle-method [6]. For accuracy the coefficient-of-determination ($$$R^2$$$) w.r.t. the reference [5], for precision the coefficient-of-variation (COV) or the standard-deviation ($$$\sigma$$$) was calculated.
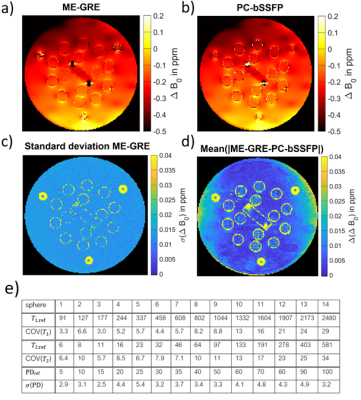
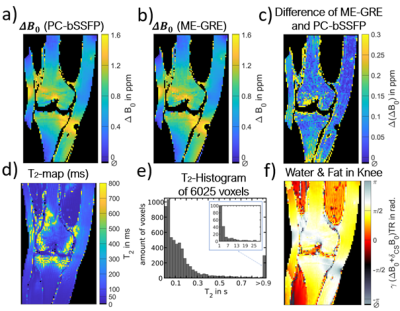
In-vivo-imaging: Knee data of a volunteer was acquired with ME-GRE and PC-bSSFP as described before [7]. Off-resonance ($$$\Delta B_0$$$ and chemical-shift) and $$$T_2$$$-quantification was performed using ORACLE and evaluated. ME-GRE and PC-bSSFP $$$\Delta B_0$$$-maps were masked for muscle-tissue to get a better comparison.

Results and Discussion

Simulations verified the high accuracy of multi-parameter quantification using ORACLE with errors below 5% for biological $$$T_1$$$ and $$$T_2$$$ (Figure 2a,b). PD and $$$\Delta B_0$$$ quantification exhibits high robustness against noise (Figure 2c,d). Parameter quantification was performed on a simple computer(2.80GHz, 32GB) for 10⁶ voxels within a second, compared with current methods that require over 2 min[8]. Experimentally estimated $$$T_1$$$ and $$$T_2$$$ values as well as PD-quantification agreed well with reference-values from the NIST-phantom with $$$R^2=[0.986, 0.993]$$$ and $$$R^2=0.986$$$, respectively (Figure 3). The COVs of $$$T_1$$$ and $$$T_2$$$ for the chosen sensitivity-range were below 10% (Figure 4e). $$$\sigma$$$ of the PD-estimation was below 5%. The $$$\Delta B_0$$$-maps extracted from PC-bSSFP compared well with neighboring $$$\Delta B_0$$$-maps obtained with ME-GRE (Figure 4). $$$\sigma$$$ of $$$\Delta B_0$$$-maps of four ME-GRE experiments performed over a 3-hour period was globally higher than the three averaged differences between neighboring ME-GRE and PC-bSSFP $$$\Delta B_0$$$-maps. Thus, $$$\Delta B_0$$$-quantification with PC-bSSFP exhibited high precision and accuracy, equivalent to ME-GRE $$$\Delta B_0$$$-quantification, whose difference was notably below $$$B_0$$$-drift-effects.
The knee $$$\Delta B_0$$$-maps obtained with ME-GRE and PC-bSSFP were in good agreement with an average error of 0.085ppm, which is in a plausible range for $$$\Delta B_0$$$-drift, susceptibility and motion (Figure 5abc). $$$\Delta B_0$$$-values of the knee were in a reasonable range of 30-250ms (Figure 5de). Outliers are attributed to the single-compartment assumption of ORACLE, which overestimates $$$T_2$$$ in the presence of other chemical species within the voxel [9]. Chemical-shift-effects allowed a visual separation between muscle and subcutaneous fat/bone-marrow with PC-bSSFP (Figure 5f). Off-resonance quantifications and chemical-shift-effects were completely decoupled from $$$T_2$$$-quantifications, making off-resonance-corrections expendable.

Conclusion

ORACLE was developed for ultra-rapid, and simultaneous $$$T_1$$$, $$$T_2$$$, $$$\Delta B_0$$$ and PD quantification. $$$T_1$$$, $$$T_2$$$, $$$\Delta B_0$$$ and PD could be quantified with high accuracy and precision. ORACLE compactifies all information content of experimental data, enabling the first PC-bSSFP signal-analysis-framework for multi-parameter quantification, while making off-resonance corrections redundant.

Acknowledgements

This study was supported by the Swiss National Science Foundation (grant number PCEFP2_194296).