Synopsis

Keywords: Quantitative Imaging, Magnetization transfer

Macromolecular proton fraction (MPF) represents the relative amount of semi-solid macromolecules involved in magnetization transfer with free water protons. In this work, we reported a novel MPF quantification method based on spin-lock for rapid MPF mapping. The total scan time for 3D brain MPF measurement can be achieved within five minutes. We demonstrated the proposed method via simulation, phantom and in vivo experiments.

Introduction

Magnetization transfer (MT) involves protons of mobile water and protons with semi-solid macromolecules¹. Macromolecular proton fraction (MPF) is one of the key parameters in quantitative MT (qMT) model², which represents the relative amount of macromolecules involved in magnetization exchange with free water protons. Several methods have been proposed to quantify MPF^3–6. Recently, a novel MPF imaging method based on spin-lock (SL), termed MPF-SL, was proposed⁶. Here we reported a novel acquisition approach for fast MPF quantification based on spin-lock which can achieve significantly reduced scan time compared to MPF-SL. We demonstrated our fast MPF-SL method via simulation, phantom and in vivo experiments.

Methods

MPF contrast using MPF-SL approach can be obtained from the difference of two groups of off-resonance spin-lock R1ρ with certain SL amplitude ω1 and frequency offset Δω⁶: $$Rmpfsl = R1ρ(ω1(2),Δω(2))-R1ρ(ω1(1),Δω(1))$$
under the condition of $$Δω(2)/ω1(2)=Δω(1)/ω1(1); Δω(i) »ω1(i)(i=1,2)$$. The magnetization during SL can be expressed as:M=M_inie^-R1ρTSL+M₀R₁cosθ/R1ρ(1-e^-R1ρTSL), where M_ini is initial magnetization before SL, M₀ is the equilibrium magnetization, R₁(=1/T₁) is the longitudinal relaxation rate of water protons, TSL is time of spin-lock, and θ=atan(ω1/Δω) . As a magnetization reset RF pulse is commonly applied for nulling magnetization at the beginning of a SL pulse sequence, M_ini can be expressed as M_ini=M₀(1-e^-R₁T_1rec), where T_1rec is recovery time after magnetization reset RF pulse.
By applying T_1rec>T₁ under the conditions of MPF-SL listed above, we can have: M₀(1-e^-R₁T_1rec)e^-R1ρTSL»M₀R₁cosθ/R1ρ(1-e^-R1ρTSL).
Accordingly, the SL signal equation can be simplified to a mono-exponential model: M≈M_inie^-R1ρTSL. As a result, MPF contrast can be obtained by only 2 acquisitions: $$Rmpfsl = R1ρ(ω1(2),Δω(2))-R1ρ(ω1(1),Δω(1))=-log(M(2)/M(1)) /TSL$$
We demonstrate our approach in brain applications. Figure 1 shows the sequence diagram. Following the ω1 and Δω selection principles in MPF-SL approach⁶, the SL parameters to quantify brain MPF are selected as: TSL 50 ms; ω1(i) 100 Hz and 500 Hz; Δω(i) 800 Hz and 4000 Hz for i = 1;2, respectively.
For the simulation study, Bloch-McConnell simulation was performed to investigate Rmpfsl using our proposed method as a function of MPF for brain tissue⁷.
All MRI scans were conducted using a 3.0 T MRI scanner (Philips Achieva, Philips Healthcare, Best, Netherlands) equipped with a 8-channel head coil (Invivo Corp, Gainesville, USA). In addition, the SL parameters used for all MRI scans were same as those mentioned above for brain MPF measurement.
Two phantom experiments were performed. The first experiment was used to validate that our proposed fast MPF-SL approach is sensitive to MPF using five agarose phantoms with concentration from 1% to 5%. The second experiment was used to validate that the proposed fast MPF-SL method is insensitive to the relaxation of water protons using agarose phantoms with and without MnCl₂ added. Imaging parameters of the fast MPF-SL method for these two phantom experiments include: resolution 2mm×2mm, slice thickness 7mm, TR/TE 2500/30 ms. Conventional MPF-SL method was also performed on phantom experiments to compare the MPF results.
In vivo study was conducted after approval by local institutional review board. MRI data was collected from two healthy volunteers and one Relapsing-Remitting Multiple Sclerosis (RRMS) patient. Imaging parameters include: FOV 250 × 250 × 144mm³, resolution 1.5 ×1.5 ×4mm³, SENSE was used in two phase-encoding directions with acceleration factors 2 and 1. B1 map was collected to quantify MPF.

Results

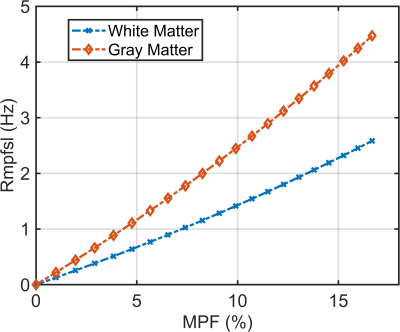
Figure 2 shows the simulation results. It shows that Rmpfsl obtained by our proposed fast MPF-SL approach is approximately a linear function of MPF. Figure 3 shows the results from first phantom study. Note Rmpfsl obtained by the fast MPF-SL method increases with agarose concentration. Figure 4 shows the results from second phantom study. Note Rmpfsl results are comparable when the agarose concentration was same, regardless of MnCl₂ concentration. Besides, Rmpfsl results are comparable when using conventional and fast MPF-SL method. Figure 5 shows the in vivo results. Note the MPF decreases at the lesions from the RRMS patient, which suggests the demyelination at these lesions. Compared to two healthy volunteers, the brain MPF value of this RRMS patient shows overall decreases.

Discussion & Conclusion

We proposed a fast MPF imaging method based on spin-lock, and demonstrated it by simulation, phantom and in vivo experiments. In contrast to the conventional MPF-SL method, imaging data can be collected using only two acquisitions under reasonable assumptions. Compared to the saturation RF pulse based approaches, spin-lock based methods do not require acquisition of T₁ map as prior knowledge for MPF calculation. Only a B1 map is needed in addition to imaging data to quantify MPF. The MPF measurement of the whole brain can be achieved within 5 minutes scan time using the proposed method. Future work includes further validation of this promising MPF mapping technique and evaluate its clinical applications in neuro diseases⁸ and beyond⁹.

Acknowledgements

This study was supported by a grant from the Innovation and Technology Commission of the Hong Kong SAR (Project MRP/046/20X).