1240
Universal modes: Calibration-free TIAMO for B1+ inhomogeneity mitigation1Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
Keywords: High-Field MRI, Body
In this work we introduce the concept of universal modes, which consists of the application of the universal pulse concept to time interleaved acquisition of modes (TIAMO). Based on simulated B1+ maps of a 16-channel body array at 10.5T, the ability to mitigate B1+ inhomogeneities is successfully demonstrated in six different human body models, targeting the pelvis.
Introduction
Ultrahigh-field MRI offers unique opportunities but also faces many challenges, such as the inhomogeneity of the transmit B1+ field due to decreased RF wavelengths. One way to overcome this limitation is to use parallel transmission (pTx) techniques which usually require the acquisition of subject-specific calibration data and the application of subsequent optimization strategies. This additional effort poses an immense challenge with respect to the widespread application of pTx, which is why the concept of universal pulses (UP) was introduced1. Originally developed for head imaging, the UP concept has been extended to the human heart at 7T2 and although most applications of UPs have focused on the use of kT-points3, the method was shown to be applicable to other RF pulse design strategies, such as multi-spokes RF pulses4,5 or SPINS6,7. In this work, we introduce the concept of universal modes (UM), which results from the application of the UP concept to time interleaved acquisition of modes (TIAMO)8, to address B1+ inhomogeneity in the human body at 10.5T.Methods
The subject-specific B1+ maps used for pulse optimization were generated from the electromagnetic simulations of a body-array consisting of 16 fractionated dipoles tuned to 447MHz using Sim4Life (Zurich Medtech, Switzerland). Six different human body models (Duke, Ella, Fats29, Glenn, Jeduk, Yoon-sun) were used with the body-array positioned around the pelvis (Figure 1). Following the non-localized least-squares TIAMO design9, subject-specific solutions were calculated according to the following minimization problem:$$\min_{x_1,~x_2,~...,~X_{N_m}}\left\{{\left\lVert\sqrt{\sum_{m=1}^{N_m}{\mid{S\cdot{x_m}}\mid}^2}-\mid\alpha\mid\right\lVert}^2\right\}$$
where $$$x_m$$$ is the $$$N_c\times1$$$ complex shimming vector (phase and magnitude) of mode $$$m$$$ with a total of $$$N_c$$$ transmit channels, $$$S$$$ is a $$$N_s\times{N_c}$$$ matrix of transmit sensitivities within a slice containing $$$N_s$$$ voxels, and $$$\alpha$$$ the target B1+ distribution.
To generate UMs, the above stated optimization was extended to include transmit sensitivities from multiple subjects by minimizing the Euclidian norm of the objective functions across different subjects.
Subject-specific as well as UMs were computed for different number of modes of up to $$${N_m}=5$$$ in MATLAB (The MathWorks, USA) with a spatially uniform target B1+ of 5.87μT. In addition, $$$N_m$$$ “default” modes were defined as shimming vectors with constant amplitude and a phase increment of $$$m\cdot{22.5^{\circ}}$$$ for the $$$m^{th}$$$ mode.
The subject-specific solutions were evaluated both for the subjects for whom they were optimized and for the other five subjects. Using a leave-one-subject-out strategy, UMs were calculated for all permutations of five subject-specific B1+ maps and consecutively applied to the unseen subject. While the subject-specific solutions when applied to the subject for whom they were optimized are inherently power-calibrated, this is not true when applying them to the other five subjects. Therefore, in these cases a simple power-calibration was performed to match the average B1+ to the target value. The same power-calibration was performed for the default modes and the UMs.
The performance of the different solutions was evaluated using the normalized root mean squared error (NRMSE).
Results
Figure 2A shows the NRMSE of the default modes, yielding a median NRMSE of 0.17 for the 1-mode case, while not showing a clear performance increase when using a higher number of modes. The subject-specific 1-mode solution reduces the median NRMSE to 0.07, which can be further improved to 0.04 by increasing the number of modes (Figure 2B). However, using more than three modes, does not yield further improvements. The performance of the subject-specific solutions applied to the other five subjects are summarized in Figure 2D, showing large variations and leading to worst-case NRMSE values of 0.20 and 0.19 for the 1-mode and 3-mode case, respectively. In contrast, the UMs (Figure 2C) reduce the worst-case values to 0.17 and 0.12 while yielding median NRMSE values of 0.11 and 0.07 for the 1-mode and 3-mode case, respectively.B1+ maps of all subjects, corresponding to the 1-mode and 3-mode cases are displayed in Figure 3. In general, the 1-mode cases fail to produce B1+ maps free of severe destructive interferences, which also holds true for the 3-mode case when using default modes (Figure 3A). While the subject-specific 3-mode solutions (Figure 3B) successfully mitigate B1+ inhomogeneities, the universal 3-mode solutions (Figure 3C) avoid severe destructive interference in the center of the body at the cost of elevated B1+ values close to the transmit elements. Quantitatively this can be seen in Figure 4, when comparing the 5th and 95th percentiles of the B1+ distributions.
Conclusion
This study shows the successful application of the UP concept to TIAMO and demonstrates the feasibility of the proposed technique to mitigate B1+ inhomogeneities. While only based on pelvis data simulated for 10.5T, UMs are expected to be applicable to other body regions such as the heart, which are more challenging in terms of acquisition of calibration data10. In addition, application at 7T should yield further improved B1+ inhomogeneity mitigation. The limitation of this study is the exclusive use of simulation data, which should be supported by in vivo measurements in the future. Furthermore, it remains to be shown that UMs can also be used for the recently proposed AMORE11 approach for mode optimization and how they can be leveraged to enhance the intrinsic SAR efficiency of TIAMO9 for improved scan efficiency.Acknowledgements
Funding was provided by NIH P41 EB027061 and NIH R01 EB029985.References
[1] Gras, V, Vignaud, A, Amadon, A, Le Bihan, D, Boulant, N (2017), Universal pulses: A new concept for calibration-free parallel transmission. Magn. Reson. Med., 77: 635-643.
[2] , , , (2021), Calibration-free pTx of the human heart at 7T via 3D universal pulses. Magn. Reson. Med., 87: 70-84.
[3] Cloos, MA, Boulant, N, Luong, M, Ferrand, G, Giacomini, E, Le Bihan, D, Amadon, A (2012), kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magn. Reson. Med., 67: 72-80.
[4] Saekho, S, Yip, C, Noll, DC, Boada, FE, Stenger, VA (2006), Fast-kz tree-dimensional tailored radiofrequency pulses for reduced B1 inhomogeneity. Magn. Reson. Med., 55: 719-724.
[5] Gras, V, Boland, M, Vignaud, A, Gerrand, G, Amadon, A, Mauconduit, F, Le Bihan, D, Stoecker, T, Boulant, N (2017), Homogeneous non-selective and slice-selective parallel-transmit excitations at 7 Tesla with universal pulses: A validation study on two commercial RF coils. PLOS ONE 12(8): e0183562.
[6] Malik, SJ, Keihaninejad, S, Hammers, A, Hajnal, JV (2012), Tailored excitation in 3D with spiral nonselective (SPINS) RF pulses. Magn. Reson. Med., 67: 1303-1315.
[7] Mooiweer, R, Clark, IA, Maguire, EA, Callaghan, MF, Hajnal, JV, Malik, SJ (2022), Universal pulses for homogeneous excitation using single channel coils. Mag. Reson. Imag., 92: 180-186.
[8] Orzada, S, Maderwald, S, Poser, BA, Bitz, AK, Quick, HH, Ladd, ME (2010), RF excitation using time interleaved acquisition of modes (TIAMO) to address B1 inhomogeneity in high-field MRI. Mag. Reson. Med., 64: 327-333.
[9] Orzada, S, Maderwald, S, Poser, BA, Johst, S, Kannengiesser, S, Ladd, ME, Bitz, AK (2012), Time interleaved acquisition of modes: An analysis of SAR and image contrast implications. Magn. Reson. Med., 67: 1033-1041.
[10] Dietrich, S, Aigner, CS, Kolbitsch, C, Mayer, J, Ludwig, J, Schmidt, S, Schaeffter, T, Schmitter, S (2021), 3D Free-breathing multichannel absolute B1+ mapping in the human body at 7T. Mag. Reson. Med., 85: 2552-2567
[11] He, X, Schmidt, S, Zbyn, S, Heluptzok, T, Moeller, S, Metzger, GJ (2022), Improved TSE imaging at ultrahigh field using nonlocalized efficiency shimming and acquisition modes optimized for refocused echoes (AMORE). Mag. Reson. Med., 88: 1702-1719.
Figures
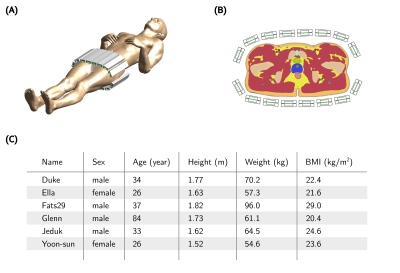
Figure 1:
(A) simulation setup of the 16-channel body-array positioned around the pelvis of the Duke model with corresponding cross-section centered on the array (B). The fractionated dipoles are positioned with a center-to-center distance of 6cm. (C) Overview of the properties of the six body models used in this study.

Figure 2:
Performance of the default modes (A), subject-specific solutions (B) and universal modes (C) in all six subjects for different number of modes. Application of the subject-specific solutions of each subject to the other five subjects (D) leads to a high variability in performance as a consequence of inter-subject variability.

Figure 3:
B1+ maps of the 1-mode and 3-mode cases of the default modes (A), the subject specific solutions (B), and the universal modes (C) displayed for all six subjects. While all 1-mode cases fail to prevent severe destructive interference, the subject-specific 3-mode solutions successfully mitigate B1+ inhomogeneities. Similarly, the universal 3-mode solutions avoid severe destructive interference in the center of the body at the cost of elevated B1+ values close to the transmit elements.

Figure 4:
Violin plots of the B1+ distributions of the 3-mode cases displayed in Figure 3. The red lines indicate the 5th and 95th percentiles. In all cases the universal modes clearly outperform the default modes leading to tighter B1+ distributions and especially avoiding severe destructive interferences.