1164
VORTEX-SS: Encoding Physics-Driven Data Priors for Robust Self-Supervised MRI Reconstruction1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Computer Science, Stanford University, Stanford, CA, United States, 4Biomedical Data Science, Stanford University, Stanford, CA, United States
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Artifacts
Deep learning (DL) has demonstrated promise for fast, high quality accelerated MRI reconstruction. However, current supervised methods require access to fully-sampled training data, and self-supervised methods are sensitive to out-of-distribution data (e.g. low-SNR, anatomy shifts, motion artifacts). In this work, we propose a self-supervised, consistency-based method for robust accelerated MRI reconstruction using physics-driven data priors (termed VORTEX-SS). We demonstrate that without any fully-sampled training data, VORTEX-SS 1) achieves high performance on in-distribution, artifact-free scans, 2) improves reconstructions for scans with physics-driven perturbations (e.g. noise, motion artifacts), and 3) generalizes to distribution shifts not modeled during training.Introduction
Deep learning (DL)-based MRI reconstruction methods have shown promise for improved image quality at higher acceleration rates and faster inference times compared to parallel imaging and compressed sensing1–3. However, DL methods are predominantly supervised and strictly require fully-sampled datasets during training4. While self-supervised approaches (e.g. SSDU5) have alleviated the need for fully-sampled scans, these methods are sensitive to distribution shifts resulting from routine acquisition-related perturbations (e.g. changes in SNR, motion artifacts) or changes in scan protocol and hardware6–8. Semi-supervised methods that leverage both fully-sampled and undersampled-only datasets like VORTEX9,10 use consistency training to reduce the requisite amount of fully-sampled training data and to improve robustness to physics-driven distribution shifts. However, these methods require access to some fully-sampled references, which cannot always be acquired.In this work, we propose VORTEX-SS, a self-supervised method for robust accelerated MRI reconstruction. VORTEX-SS combines SSDU and VORTEX to train robust networks without fully-sampled references. We demonstrate VORTEX-SS can generalize to reconstructing scans with multiple sources of distribution shift, including changes in SNR, patient motion, and anatomy.
Theory
VORTEX-SS complements the masked training strategy in SSDU with physics-aware, augmentation-based consistency training to encode physics-driven data priors (schematic-Fig.1).Training Strategy: Consider dataset $$$D$$$ without any fully-sampled scans. $$$y^i_\Omega$$$ is the k-space for example $$$i$$$ acquired with undersampling mask $$$\Omega$$$ and encoding operator $$$A_\Omega^i$$$. Following SSDU, VORTEX-SS splits the acquired k-space into two disjoint sets — $$$y_\Theta^i=\Theta y_\Omega^i$$$ and $$$y_\Lambda^i=\Lambda y_\Omega^i$$$ (where $$$\Theta\cup\Lambda=\Omega,\;\Theta\cap\Lambda=\emptyset$$$), which are used for data consistency in the model and the training loss, respectively. The masked loss is$$L_{masked}^i=\mathcal{L}\Bigl(y_\Lambda^i,A_\Lambda^i\bigl(f_\theta(y_\Theta,A_\Theta^i)\bigl)\Bigl)\;\;\;\;\;\text{(1)}$$where $$$\mathcal{L}$$$ is the training loss and $$$f_\theta$$$ is the DL model. Additionally, VORTEX-SS augments the k-space with physics-driven augmentations $$$g$$$ and generates reconstructions for both the non-augmented and augmented k-space. Consistency between these reconstructions is enforced to build invariance to the modeled perturbations (Eq.2).$$L_{consistency}^i=\mathcal{L}\Bigl(f_\theta\bigl(y^i_\Omega,A^i_\Omega\bigl),f_\theta\bigl(g(y_\Omega^i,A_\Omega^i),A^i_\Omega\bigl)\Bigl)\;\;\;\;\;\text{(2)}$$The total loss is the weighted sum of the masked and consistency losses (Eq.3).$$\min_\theta\sum_i^{|D|}L^i_{masked}+\lambda L^i_{consistency}\;\;\;\;\;\text{(3)}$$Augmentations ($$$g$$$): Augmentations modeled after MRI physics can emulate real-world distribution shifts and reduce overfitting to the training data distribution. We model two physics-based distribution shifts: 1) noise artifacts with additive complex-valued Gaussian noise with standard deviation $$$\sigma$$$ and 2) motion artifacts for 1D translational motion perturbations with phase-shift amplitude $$$\alpha$$$ (Fig.2). VORTEX-SS also supports composing multiple augmentations (e.g. noise+motion).
Methods
19 fully-sampled 3D fast-spin-echo scans (mridata.org11) were split into 14, 2, and 3 scans (4480, 640, and 960 slices) for training, validation, and testing, respectively. Data was retrospectively accelerated at 12x using Poisson Disc undersampling with a 20x20 calibration region to simulate undersampled scans.We compared VORTEX-SS to self-supervised method SSDU5 and supervised training with noise (Supervised+Aug (Noise)) and motion (Supervised+Aug (Motion)) augmentations. VORTEX-SS variants were trained with noise (VORTEX-SS (Noise)), motion (VORTEX-SS (Motion)), and both noise and motion (VORTEX-SS (Physics)) augmentations. Supervised networks were trained on the dataset where all scans were fully-sampled; VORTEX-SS and SSDU were trained on undersampled-only data. All models used a proximal-gradient-descent unrolled architecture with eight residual blocks12. Loss function, learning rate, masking ratio, and augmentation hyperparameters for baseline models were tuned with the validation dataset. Image quality was measured using complex peak-signal-to-noise ratio (cPSNR), structural similarity (SSIM), and normalized root-mean-square error (nRMSE).
We evaluated VORTEX-SS on distribution shifts that were both seen and unseen during training. First, we simulated perturbations among test scans at multiple noise ($$$\sigma_{test}$$$) and motion ($$$\alpha_{test}$$$) levels. Second, to understand how methods generalize to unseen sources of distribution shifts, self-supervised methods, which were trained on the mridata 3D FSE knee dataset, were evaluated on the 2D fastMRI brain dataset13,14. This cross-dataset evaluation considers the scenario of multiple sources of distribution shift, including anatomy (knee→brain), field strength (3T→1.5T), acceleration factor (12x→4x), sequence type (3D FSE→2D FSE), undersampling pattern (Poisson Disc→random 1D), among others.
Results
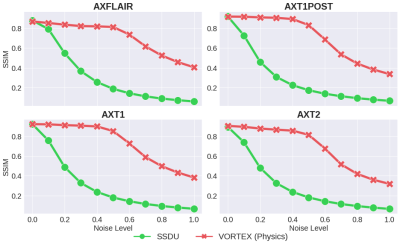
Compared to SSDU, VORTEX-SS substantially improved performance in low-SNR ($$$\sigma_{test}>0$$$) and motion-corrupted ($$$\alpha_{test}>0$$$) settings across all metrics without reducing performance on in-distribution ($$$\sigma_{test}=\alpha_{test}=0$$$) scans (Fig.3). VORTEX-SS matched the performance of augmentation-based supervised methods among low-SNR scans and recovered >70% of the performance of supervised models among motion-corrupted scans (Fig.3). VORTEX-SS maintained similar visual image quality to supervised methods in low-SNR and motion-corrupted settings (Fig.4). VORTEX-SS trained with both noise and motion augmentations performed comparably to VORTEX-SS models trained separately on these augmentations (Fig.3,4). VORTEX-SS also generalized to high-SNR and low-SNR settings among all acquisition types in the fastMRI brain dataset (Fig.5).Discussion
Expectedly, incorporating physics-driven augmentations during training increases robustness for reconstructing scans under these perturbations. However, VORTEX-SS also generalized between datasets, which consisted of distribution shifts that were not modeled during training. These results suggest that physics-driven augmentations for consistency regularization may be beneficial for generalizing to distribution shifts that are difficult to model.Despite being trained with only undersampled training data, VORTEX-SS matched the performance of supervised augmentation methods in out-of-distribution settings. VORTEX-SS also demonstrated that physics-driven augmentations can be composed to increase robustness to multiple distribution shifts without sacrificing performance on in-distribution scans. This is critical for reconstructing scans where the extent of distribution shift is unknown.
Conclusion
We propose VORTEX-SS, a self-supervised, consistency-based reconstruction method capable of reconstructing scans under multiple sources of distribution shift without any fully-sampled training data.Acknowledgements
Research support provided by NIH R01 AR077604, NIH R01 EB002524, NIH K24 AR062068, NSF-GRFP 1656518, DOD-NDSEG ARO, Precision Health and Integrated Diagnostics Seed Grant from Stanford University, Stanford Artificial Intelligence in Medicine and Imaging GCP grant, Stanford Human-Centered Artificial Intelligence GCP grant, GE Healthcare, and Philips.References
1. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated {MRI} data. Magn Reson Med. 2017;79(6):3055-3071. doi:10.1002/mrm.26977
2. Sandino CM, Lai P, Vasanawala SS, Cheng JY. Accelerating cardiac cine MRI using a deep learning‐based ESPIRiT reconstruction. Magn Reson Med. 2021;85(1):152-167. doi:10.1002/mrm.28420
3. Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: Proceedings - International Symposium on Biomedical Imaging. Vol 2016-June. ; 2016. doi:10.1109/ISBI.2016.7493320
4. Hammernik K, Schlemper J, Qin C, Duan J, Summers RM, Rueckert D. Systematic evaluation of iterative deep neural networks for fast parallel MRI reconstruction with sensitivity-weighted coil combination. Magn Reson Med. 2021;86(4). doi:10.1002/mrm.28827
5. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med. 2020;84(6). doi:10.1002/mrm.28378
6. Darestani MZ, Chaudhari AS, Heckel R. Measuring Robustness in Deep Learning Based Compressive Sensing. In: Meila M, Zhang T, eds. Proceedings of the 38th International Conference on Machine Learning. Vol 139. Proceedings of Machine Learning Research. PMLR; 2021:2433-2444. https://proceedings.mlr.press/v139/darestani21a.html.
7. Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, Sodickson DK. Assessment of the generalization of learned image reconstruction and the potential for transfer learning. Magn Reson Med. 2019;81(1):116-128. doi:10.1002/mrm.27355
8. Chaudhari AS, Sandino CM, Cole EK, et al. Prospective Deployment of Deep Learning in MRI: A Framework for Important Considerations, Challenges, and Recommendations for Best Practices. J Magn Reson Imaging. 2021;54(2):357-371. doi:10.1002/jmri.27331
9. Desai AD, Gunel B, Ozturkler B, et al. VORTEX: Physics-Driven Data Augmentations Using Consistency Training for Robust Accelerated {MRI} Reconstruction. In: Medical Imaging with Deep Learning. ; 2022. https://arxiv.org/abs/2111.02549.
10. Desai AD, Ozturkler BM, Sandino CM, et al. Noise2Recon: Enabling Joint MRI Reconstruction and Denoising with Semi-Supervised and Self-Supervised Learning. arXiv Prepr arXiv211000075. 2021. https://arxiv.org/abs/2110.00075.
11. Ong F, Amin S, Vasanawala S, Lustig M. Mridata. org: An open archive for sharing MRI raw data. In: Proc. Intl. Soc. Mag. Reson. Med. Vol 26. ; 2018:1.
12. Sandino CM, Cheng JY, Chen F, Mardani M, Pauly JM, Vasanawala SS. Compressed Sensing: From Research to Clinical Practice with Deep Neural Networks: Shortening Scan Times for Magnetic Resonance Imaging. IEEE Signal Process Mag. 2020;37(1):117-127. doi:10.1109/MSP.2019.2950433
13. Muckley MJ, Riemenschneider B, Radmanesh A, et al. Results of the 2020 {fastMRI} Challenge for Machine Learning {MR} Image Reconstruction. {IEEE} Trans Med Imaging. 2021:1. doi:10.1109/tmi.2021.3075856
14. Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. 2018:1-29. http://arxiv.org/abs/1811.08839.
Figures
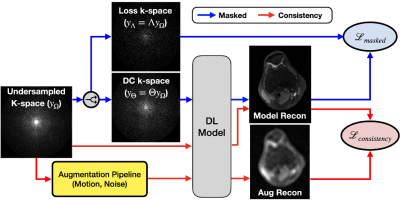
Fig.1: The VORTEX-SS schematic. VORTEX-SS complements the masked training strategy in SSDU (blue pathway) with self-supervised training (red pathway) which enforces consistency between reconstructions of unsupervised k-space and their augmented counterparts. Data augmentations, such as additive noise and patient motion, are designed to be consistent with the physics of the imaging systems. The total loss is the weighted sum of the masked ($$$L_{masked}$$$) and ($$$L_{consistency}$$$) losses.
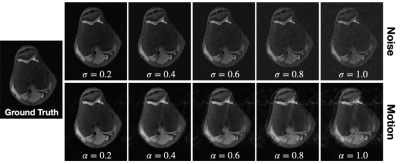
Fig.2: Examples of physics-based noise (top) and 1D translational motion (bottom) perturbations applied at different extents (noise: $$$\sigma$$$, motion: $$$\alpha$$$) to a fully-sampled image. Acquired k-space samples are corrupted with additive complex-valued Gaussian noise with standard deviation $$$\sigma$$$. Multi-shot 1D translational motion perturbations are modeled as random phase shifts with maximum amplitude $$$\alpha$$$.
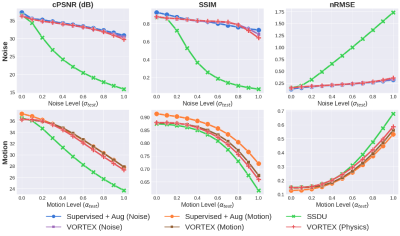
Fig.3: Model performance at varying noise (top) and motion (bottom) extents. All VORTEX-SS models outperformed SSDU in out-of-distribution settings ($$$\sigma_{test}$$$, $$$\alpha_{test}$$$) and matched performance of augmentation-based supervised methods (Supervised+Aug), which are trained with fully-sampled scans. Noise and motion augmentations can be combined in VORTEX-SS (i.e. VORTEX-SS (Physics)) without reducing performance on in-distribution scans or sacrificing robustness to either perturbation.
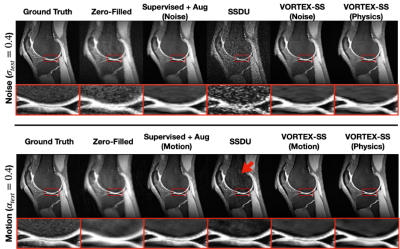
Fig.4: Sample reconstructions (sagittal reformat) for scans with low-SNR (top) and motion artifacts (bottom) using zero-filled SENSE, augmentation-based supervised methods, SSDU, and VORTEX-SS. VORTEX-SS (Physics) uses noise and motion augmentations. SSDU amplified noise and suffered from residual motion ghosting (red arrow). VORTEX-SS suppressed these artifacts, recovered fine structures, such as the femoral-tibial cartilage boundary (inset images), and had similar image quality metrics to supervised baselines.