1163
Simultaneous Motion Compensation and Image Reconstruction During Acquisition of 3D Radial MRI
Fatih Calakli1,2, Tess E. Wallace1,2, and Simon K. Warfield1,2
1Computational Radiology Laboratory, Boston Children's Hospital, Boston, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States
1Computational Radiology Laboratory, Boston Children's Hospital, Boston, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States
Synopsis
Keywords: Motion Correction, Brain
High-resolution, 3D structural scans are susceptible to patient motion as they take several minutes or more to acquire. Radial MRI acquisitions are emerging as a motion-robust alternative to Cartesian trajectories. Most approaches involve co-registration of navigator images once the acquisition is complete. However, the time needed for co-registration of navigator images, coupled with the long reconstruction times required for high-resolution NUFFT, is a challenge for integration of motion-compensated non-Cartesian imaging into clinical protocols. In this work we developed a motion-compensated online gridding algorithm to perform adaptive motion compensated reconstruction overlapped with the acquisition.Introduction
Head motion during MRI poses a challenge for acquiring high-quality diagnostic images, often necessitating repeat scans or the use of sedation in patients who have difficulty holding still. Radial MRI acquisitions are emerging as a motion-robust alternative to Cartesian trajectories as motion artifacts are less severe and they provide an opportunity for rigid-body head motion tracking from the data1. Most approaches for radial self-navigation involve binning data into fixed-width subsets of spokes and estimating motion parameters via co-registration of navigator images once the acquisition is complete. However, the time needed for reconstruction and co-registration of navigator images, coupled with the long reconstruction times required for high-resolution NUFFT2, is a challenge for integration of motion-compensated non-Cartesian imaging into clinical protocols. In this work we (i) develop a method for real-time motion monitoring during radial MRI acquisitions; (ii) use a fast gridding algorithm that does not require prior knowledge of the trajectory; and (iii) update the motion-compensated gridding reconstruction during the acquisition, in order to perform adaptive motion compensated reconstruction overlapped with the acquisition.Methods
Estimation of motion parameters:It is well known that a set of radial spokes can be used to estimate center of mass (CoM) using the Fourier Slice theorem. Instead of calculating only one CoM signal based on a short duration fixed size running window, we generate another CoM signal based on a long duration window of variable size. The difference of the short and long term CoM estimates gives a distinguishing motion score for every spoke as shown in Figure 1c. As the motion signal is generated, motion state changes are detected and that information is used to adaptively split spokes into mutually exclusive subsets. Each subset is reconstructed (via NUFFT) to generate a low resolution image, and registered with respect to the image reconstructed from the first subset.
Simultaneous gridding:
The gridding problem can be formulated as the solution of the following linear system:
\begin{equation}\Phi^\mathsf{T}\Phi\mathrm{\hat{X}}=\Phi^\mathsf{T}\mathrm{X},\end{equation}
where $$$\Phi$$$ is the gridding operator, and unknown $$$\mathrm{\hat{X}}$$$ is the Cartesian approximation to the non-uniform k-space measurements $$$\mathrm{X}$$$. The left and the right hand side of the linear system can be updated using the motion information estimated in the previous step as k-space samples are acquired. The solution of the linear system is only needed at the end of the scan.
Validation:
To validate the proposed approach, three volunteers were scanned at 3T (MAGNETOM Prisma; Siemens Healthcare, Erlangen, Germany) using a 64-channel head coil after obtaining informed consent. A product GRE sequence was modified to acquire radial data with a pseudo-random 3D golden angle sampling pattern to generate a set of spatially and temporally uniformly distributed spokes, which allows images to be reconstructed from arbitrary numbers of k-space lines. A T1-weighted structural image was acquired with TR/TE = 8/2.7 ms; FA = 30°; FOV = 240 mm; 1 mm isotropic resolution; RBW = 300 Hz/px; 48k spokes; total acquisition time 6.4 minutes. The volunteer was instructed to reposition their head every 60 s during the scan to create a motion-corrupted dataset. Images were reconstructed with (i) no motion compensation; (ii) fixed-subset alignment of spokes and (iii) the proposed adaptive method.
Results
Figure 1 shows the motion signals generated during data acquisition. The short term (Fig. 1a) fixed window size CoM estimates signal abrupt changes in motion state when compared to the long term (Fig. 1b) variable window size CoM estimates (motion score/signal in Fig. 1c). Figure 2 shows the images reconstructed by the method where only motion compensation overlaps with the acquisition. That is, motion parameters are estimated by co-registering navigator images during the scan, and image reconstruction is performed after the scan is complete (via conventional NUFFT). Figure 3 shows the images reconstructed by the method where motion compensation and image reconstruction are simultaneously performed during the acquisition. The method which uses conventional NUFFT (applied retrospectively with density compensation weights) performs slightly better, but comes with 2.2 minutes extra computation time (Table 1 - 2nd vs 3rd column) on average. However, this is still 2.7 minutes faster than the conventional pipeline (Table 1 - 1st column) where motion compensation and image reconstruction are both performed after the scan ends.Discussion
In this work, we have proposed methods to perform motion compensated reconstruction overlapped with the acquisition using a fast gridding algorithm that does not require prior knowledge of the non-Cartesian trajectory. The ability to readily generate a target image accelerates the integration of motion-compensated non-Cartesian imaging into clinical protocols. In addition, we have presented a practical method to generate a real-time motion signal during 3D radial data acquisition using CoM estimation to prospectively split the data into adaptive subsets for alignment. The proposed adaptive method provides improved motion compensation compared to aligning fixed-size subsets of spokes.Conclusion
Our proposed method for overlapping motion compensation and reconstruction with the MRI acquisition may be deployed on the scanner to achieve real-time motion monitoring and adaptive motion-compensated reconstruction during the scan. Increasing the clinical utility of motion-compensated radial imaging could, in turn, improve scan efficiency and clinical workflows and could help reduce patient rescans, recalls and the use of sedation.Acknowledgements
This work was supported in part by the NIH under award numbers S10 OD025111 and R01 EB019483.References
- Kecskemeti, S. et al. Robust motion correction strategy for structural MRI in unsedated children demonstrated with 3D radial MPnRAGE. Radiology 289, 509–516 (2018).
- Fessler, Jeffrey A., and Bradley P. Sutton. "Nonuniform fast Fourier transforms using min-max interpolation." IEEE transactions on signal processing 51.2 (2003): 560-574.
Figures
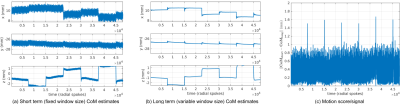
Figure 1. (a) Short term CoM estimates based on using 50 past spokes, (b) Long term CoM estimates based on using past spokes after the last detected motion incidence, (c) Motion monitoring based on the difference of short and long term CoM estimates (6 peaks 7 motion states are detected successfully, and spokes associated with each state are used to estimate 6dof motion parameters)
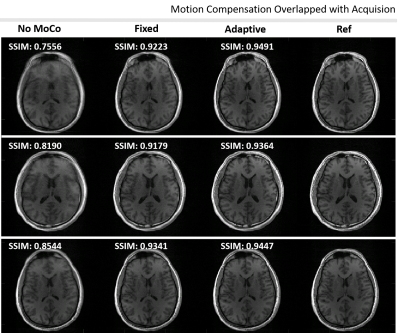
Figure 2. Quality assessment of images reconstructed. Motion parameters are estimated by co-registering navigator images during the scan, and reconstruction is performed retrospectively via conventional NUFFT. (a) Image reconstruction with no motion compensation. (b) Image reconstruction based on aligning ten low resolution images reconstructed from fixed-size subsets of spokes, (c) Image reconstruction based on aligning seven low resolution images reconstructed from automatically generated variable size subsets, (d) Ground truth reconstruction.
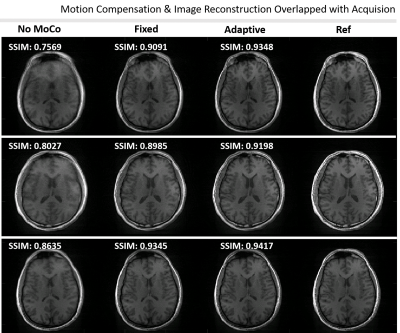
Figure 3. Quality assessment of images reconstructed. Motion compensation and image reconstruction are performed simultaneously with acquisitions by the proposed gridding strategy. From left to right: Image reconstruction with no motion compensation; Image reconstruction based on aligning ten low resolution images reconstructed from fixed-size subsets of spokes; Image reconstruction based on aligning seven low resolution images reconstructed from automatically generated variable size subsets; Ground truth reconstruction.
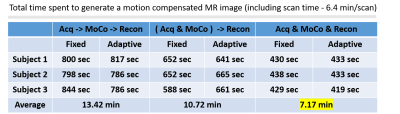
Table 1. Timing comparison of motion compensated image generation pipelines including the scan time - 6.4 min/scan. First column is the traditional pipeline where motion compensation and image reconstruction are performed sequentially after the scan. Second column shows the timings where the motion compensation overlapped with the acquisition. The last column shows where both the motion compensation and image reconstruction are overlapped with the acquisition.
DOI: https://doi.org/10.58530/2023/1163