1158
Using SMASH Spatial Harmonics to Slice-Encode Outflow Artefacts in bSSFP Imaging1Radiology, The University of California, Los Angeles, Los Angeles, CA, United States
Synopsis
Keywords: Artifacts, Cardiovascular, bSSFP, parallel imaging, spatial harmonics, Cine, Outflow effects
In the present of through plane flow in 2D bSSFP imaging, we used the variation coil sensitivity profile along the through-slice direction to estimate the spatial harmonics needed to slice-encode for outflowing spins. Estimating the outer partitions unfolded the outflowing spins from the target center slice with a faster acquisition time than our previous slice-encoding technique.INTRODUCTION
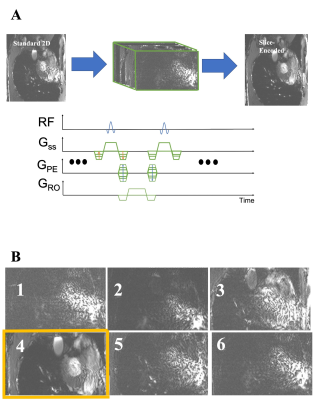
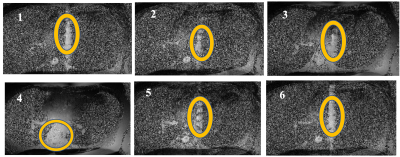
The sensitivity of 2D-bSSFP to flow effects has been extensively explored over the past two decades[ 1-4]. These effects have been shown to represent the coherent sum of off-resonant outflowing spins, ultimately leaving a 3D signal footprint on a 2D acquisition. By default, the outflowing spins project onto the 2D slice of interest and may introduce confounding signal. We previously treated this as an aliasing problem along the slice’s direction and applied a through-slice phase encoding (“slice-encoding”) scheme to encode the space beyond the excited slice [5]. This effectively unfolds the outflowing spins out of the target slice. A summary of our slice-encoded method is illustrated in Figure 1, inspired by Lu et al’s slice encoding method for metal artifacts[6]. Our previous work experimentally verified the outflowing signal profile that Markl et al initially showed when introducing this problem. Unfortunately, the scan time scales linearly with the number of acquired slice-encoding steps. For example: experiments with six encoding steps require a 20 second breath-holds to localize for outflowing spins. The location outflowing spins is encoded by the coil-sensitivity variation along the slice-select’s direction, with an example being shown in Figure 2. As such this can be exploited when trying to localize for the outflow effects as an alternative to phase encoding. Prior work has demonstrated acceleration using a combination of phase-encoding and SENSE parallel imaging [7]. In the present abstract, we propose carrying out the standard 2D bSSFP scan with no additional slice-encoding steps, relying on the slice-encoded coil calibration scan to create a small number of spatial harmonics. This approach is inspired by the SMASH-based methods [8], including VD-AUTO-SMASH [9], Coil-by-coil SMASH reconstruction[ 10], and GRAPPA[11].METHODS
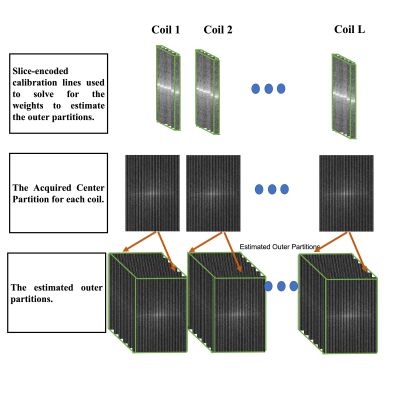
Measurements were performed on a 3T system (Prisma; Siemens) with informed consent that was approved by an internal review board. 2D cardiac cines were acquired in the horizontal long axis (HLA) orientation with the following parameters: TE/TR = 1.58/3.61 ms, 977 Hz/pixel readout bandwidth, FA = 60°, a 1.6x1.6 mm in-plane resolution, a 256x184 in-plane matrix, GRAPPA-2X, and 12 views-per-segment. A phased array and table coil, totaling to 34 channels, was used. In addition to the segmented 2D bSSFP cine, a low-resolution calibration scan with six slice-encoding steps was also acquired, with 12 in-plane fully sampled PE steps. Acquisition parameters were the same otherwise. The calibration scan was used to solve for the weights needed to estimate spatial harmonics. The resolution of the estimated k-space lines along the slice-encoding axis was $$$\Delta k_z = \frac{1}{N_s S_T}$$$ , with $$$S_T$$$ being the slice thickness and $$$N_s$$$ is the number of desired slice-encoding steps. With a total of $$$L$$$ coils, the encoding step of a coil $$$j$$$ was solved for using $$$\sum_{l=1} ^{L} {n^{m, j}_l S_l(k_x, k_y)} = S_j(k_x, k_y, m \Delta k_z)$$$, where $$$m$$$ indicates the desired spatial harmonics along the slice’s direction. With the acquired 2D scan serving as the $$$k_z = 0$$$ plane, the reference lines were used to solve for the $$$m = \pm 1, \pm 2, and -3 $$$ harmonics, as illustrated in Figure 3. Both acquisitions were acquired in a single eight-second breath-hold.RESULTS
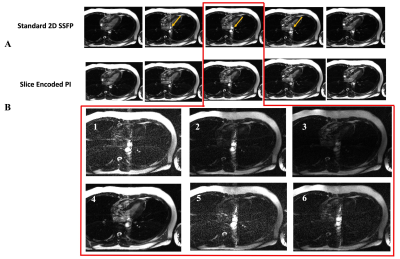
Figure 4 displays our results. Part A shows five of the sixteen acquired frames that capture the peak systolic period of the cardiac cycle, which is when outflow effects are most pronounced. The top array shows the standard 2D images while the bottom shows the corresponding center images of the estimated slice-encoding data. The golden arrow on the top images point to the outflow artifacts that are significantly reduced after estimating for the slice-encoding steps. Part B shows the estimated outer partitionsDISCUSSION AND CONCLUSION
To reduce the acquisition time of our slice-encoding anti-aliasing method in bSSFP imaging, we estimated the outer slice-encoding steps by exploiting the variable array coil sensitivity profile along the slice direction. A calibration scan is required that features slice-encoding steps along with the standard 2D acquisition in a single eight-second breath-hold. With the outer partitions estimated, a significant portion of the outflowing spins were able to be unfolded from the target center slice. Compared to the our previous approach, the new method achieves a four-fold reduction in acquisition time, making the method practical for clinical applications.Acknowledgements
No acknowledgement found.References
1. Markl M, Alley M, Elkins C, and Pelc N. Flow Effects in Balanced Steady State Free Precession Imaging. Magnetic Resonance in Medicine. 2003; 50(5): 982-903.
2. Markl M and Pelc NJ. On Flow Effects in Balanced Steady-State Free Precession Imaging: Pictorial Description, Parameter Dependence, and Clinicial Implications. Journal of Magnetic Resonance Imaging. 2004; 20(4): 697-705.
3. Storey P, Li W, Chen Q, and Edelman RR. Flow Artifacts in Steady-State Free Precession Cine Imaging. Magnetic Resonance in Medicine. 2004; 51(1): 115-122.
4. Schar M, Kozerke S, Fischer S, and Boesiger P. Cardiac SSFP Imaging at 3 Tesla. Magnetic Resonance in Medicine. 2004; 51 (4): 799-806.
5. Ali F, Bydder M, Han H, Wang D, Ghodrati V, Gao C, Prosper A, Nguyen KL, Finn JP, Hu P. Slice encoding for the reduction of outflow signal artifacts in cine balanced SSFP imaging. Magn Reson Med. 2021 Oct;86(4):2034-2048. doi: 10.1002/mrm.28858. Epub 2021 May 31. PMID: 34056755.
6. Lu W, Pauly KB, Gold GE, Pauly JM, and Hargreaves BA. SEMAC: Slice Encoding for Metal Artifact Correction in MRI. Magnetic Resonance in Medicine. 2009; 62(1): 66-76.
7. Otazo, R., Nittka, M., Bruno, M., Raithel, E., Geppert, C., Gyftopoulos, S., Recht, M. and Rybak, L. (2017), Sparse-SEMAC: rapid and improved SEMAC metal implant imaging using SPARSE-SENSE acceleration. Magn. Reson. Med., 78: 79-87. https://doi.org/10.1002/mrm.26342
8. Sodickson, D.K. and Manning, W.J. (1997), Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radiofrequency coil arrays. Magn. Reson. Med., 38: 591-603. https://doi.org/10.1002/mrm.1910380414
9. Heidemann RM, Griswold MA, Haase A, Jakob PM. VD-AUTO-SMASH imaging. Magn Reson Med. 2001 Jun;45(6):1066-74. doi: 10.1002/mrm.1141. PMID: 11378885.
10. McKenzie CA, Ohliger MA, Yeh EN, Price MD, Sodickson DK. Coil-by-coil image reconstruction with SMASH. Magn Reson Med. 2001 Sep;46(3):619-23. doi: 10.1002/mrm.1236. PMID: 11550258.
11. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002 Jun;47(6):1202-10. doi: 10.1002/mrm.10171. PMID: 12111967.
Figures