Synopsis

Keywords: Artifacts, Relaxometry

Cardiac pulsation enhances the noise level in MR images of the brain and reduces the sensitivity of the data in studies of brain disease. We propose two data acquisition strategies that mitigate cardiac-induced noise in quantitative brain maps of the MRI parameter R₂*. The first strategy sets the number of samples at each k-space location according to the local level of cardiac-induced noise. The second strategy adjusts data acquisition in real-time to acquire the data most sensitive to cardiac-induced noise during the diastolic period of the cardiac cycle.

Introduction

The transverse relaxation rate R₂* correlates with e.g. iron and myelin concentration in brain tissue and enables the monitoring of microscopic disease-related changes in patients^1-3. However cardiac pulsation enhances the noise level in R₂* maps of the brain and reduces the sensitivity of the data to brain tissue changes⁴. No data acquisition strategy has been shown to mitigate cardiac-induced noise in R₂* maps of the brain. Raynaud et al.⁵ quantified the effect of cardiac-related noise on R₂* estimates and identified the affected k-space regions. From these characteristics, we propose data acquisition strategies optimized to mitigate cardiac-induced noise in R₂* maps of the brain. The first mitigation strategy sets the number of samples at each k-space location according to the local level of cardiac-induced noise⁶. The alternative strategy synchronizes prospectively in real-time the acquisition of the most cardiac-sensitive data around the diastolic period of the cardiac cycle^7-10.

Methods

Multi-echo data was acquired on 5 participants using a 3T scanner (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) and a customized 3D Cartesian FLASH sequence (repetition time TR =40ms; echo times =2.34ms to 35.10ms with 2.34ms spacing). The pixel size was 2mm and 4mm along the readout and phase-encode directions. Data was acquired continuously for one hour using a sampling kernel optimized to mitigate spurious non-cardiac noise. The data were retrospectively distributed across 12 bins according to the phase of the cardiac cycle at which they were acquired, resulting in a fully sampled five-dimensional datasets (three spatial dimensions, echo time, phase of the cardiac cycle) that enabled the analysis of cardiac pulsation effects on brain R₂* maps⁵.
We conducted numerical simulations of cardiac pulsation effects in multi-echo 3D (i.e. 4D) data normally acquired to compute brain R₂* maps. This data was obtained by picking data from the 5D model of cardiac-induced noise according to the k-space sampling trajectory (i.e. k-space coordinates of the data acquired consecutively in time) and a log of cardiac pulsation obtained experimentally using a pulse-oximeter. The ability of the sampling trajectories to mitigate cardiac-induced noise was assessed from the standard deviation of the R₂* maps and their goodness of fit (RMSE) across repetitions with the same acquisition but different recordings of cardiac pulsation.
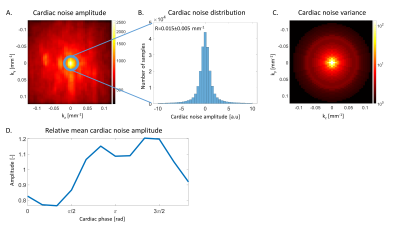
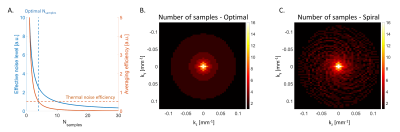
Figure 1 shows characteristics of cardiac-induced noise in k-space data. The amplitude of cardiac-induced noise is radially distributed and is highest around the origin⁵ (Figure 1A). Within a given radius, cardiac-induced noise follows a Gaussian distribution (Figure 1B). Figure 1C shows the variance of this distribution, estimated within all circles centred on the origin. From this result, we defined a mitigation strategy from the number of samples averaged at each k-space location (N_samples) that produces the most efficient reduction in effective noise level. This is illustrated in figure 2A for a voxel with cardiac-induced noise variance 10 times that from thermal noise (decrease in effective noise level ~1/N_samples). At N_samples =4 an additional sample decreases the effective noise level by 0.5 (‘efficiency’), identical to a voxel dominated by thermal noise where only 1 sample is acquired. The most efficient number of samples in this case is therefore N_samples =4. Figure 2B shows the distribution of the number of samples for efficient reduction in the effective noise level, which can be best reproduced with a Cartesian pseudo-spiral trajectory with 68 spiral arms with 63 multi-echoes readouts each, and a radial sampling density matched to the optimal number of samples (Figure 2C).
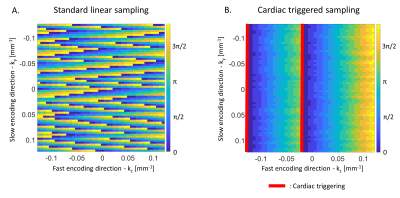
With a standard 2D linear trajectory the k-space centre, most sensitive to cardiac-induced noise, is acquired across all phases of the cardiac cycle (Figure 3A). While the cardiac phase varies smoothly along the fast encoding direction where data points are acquired consecutively every TR =40ms, abrupt changes in the cardiac phase take place along the slow encoding direction, which leads to aliasing in the reconstructed images^11,12. However, cardiac-induced noise is strongest around the systolic period of the cardiac cycle ($$$\phi_c=[\pi/2,3\pi/2]$$$) and lowest around the diastolic period ($$$\phi_c=[3\pi/2,\pi/2]$$$, Figure 1D). From this, we defined a real-time mitigation strategy in which the k-space centre data is acquired during the diastole (Figure 3B), minimizing both the level of cardiac-induced noise and aliasing.

Results

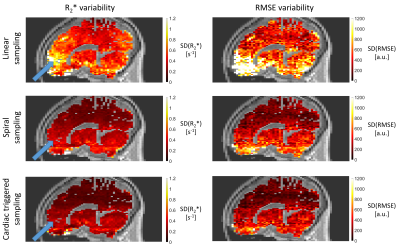
Compared to standard linear sampling, the spiral and cardiac-triggered trajectories reduce the variability of R₂* by 31% and 52% and of RMSE by 30% and 50% respectively, on average over the whole brain (Figure 4). The increase in scan time for the two mitigation strategies was 72% and 29%. Both strategies lead to a strong reduction in aliasing of cardiac-induced noise from blood vessels (e.g., circle of Willis) into the brain (Figure 4, blue arrows).

Discussion & conclusion

From the characteristics of cardiac-induced noise in k-space, we propose two sampling strategies to mitigate cardiac pulsation effects on brain R₂* maps. The first strategy adjusts the number of samples at each k-space location to reduce the effective noise level efficiently. The alternative strategy restricts the acquisition of the sensitive k-space regions during the diastolic period of the cardiac cycle. Our results suggest that the cardiac-triggered strategy reduces cardiac-induced noise in brain R₂* maps most efficiently.

Acknowledgements

No acknowledgement found.