Synopsis

Keywords: Quantitative Imaging, Quantitative Imaging

MR spectroscopic imaging (MRSI) without water suppression provides a unique opportunity to use the unsuppressed water spectroscopic signals for T₁ and T₂ mapping. This work presents a new image reconstruction method for reconstructing the T₁/T₂ maps from the highly sparse MRSI data. This method uses a novel generalized series-assisted low-rank tensor model to absorb the high-quality reference MRSI images to constrain the spatial-spectral-parametric variations. Experimental results demonstrated very encouraging reconstruction performance.

Introduction

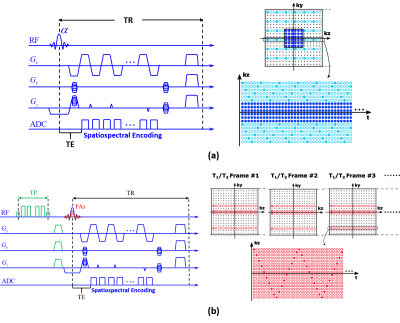
MR spectroscopic imaging (MRSI) and quantitative parametric mapping are common imaging tools that provide complementary insights into tissue properties and disease changes^1,2. In practice, these two imaging modalities are performed using different sequences, leading to prohibitively long scan time (> 30 min). Recently, an emerging MRSI technique called SPICE has demonstrated a unique capability of simultaneous acquisition of tissue metabolites and relaxation parameters³. As shown in Fig. 1, in addition to the backbone non-water-suppressed MRSI data for metabolic imaging^4-8, SPICE acquires a series of additional data frames with varying flip angles and T₂ preparation pulses for T₁/T₂ mapping³. These auxiliary data sample the $$$(\boldsymbol{k},t)$$$-space very sparsely (with an acceleration factor of 388), thereby only adding a tiny amount of scan time (1 min). However, the extreme sparse sampling poses great challenge for image reconstruction. This work addresses this problem using a model-based approach. A novel generalized series (GS)-assisted low-rank tensor model is proposed to effectively incorporate the spectral and spatial priors in the metabolic imaging signals, enabling high-quality T₁/T₂ reconstruction from highly sparse data. The proposed method has been evaluated using both simulated and experimental data, producing impressive results.

Methods

Problem Formulation
The specific image reconstruction problem addressed here can be formulated as follows:
$$\hspace{10em}\text{Given }d(\boldsymbol{k},t,T)=\int\rho(\boldsymbol{x},t,T)e^{-i2\pi\boldsymbol{k}\boldsymbol{x}}d\boldsymbol{x}+\xi(\boldsymbol{k},t,T)\text{ and }\rho_{\text{ref}}(\boldsymbol{x},t),\\{\hspace{15em}}\text{determine }\rho(\boldsymbol{x},t,T).\hspace{23em}(1)$$
In Eq. (1), $$$\rho(\boldsymbol{x},t,T)$$$ denotes the desired image function of spatial ($$$\boldsymbol{x}$$$), spectroscopic ($$$t$$$), and parametric ($$$T$$$) variations, $$$d(\boldsymbol{k},t,T)$$$ the acquired T₁/T₂ imaging data, $$$\xi(\boldsymbol{k},t,T)$$$ the measurement noise, and $$$\rho_{\text{ref}}(\boldsymbol{x},t)$$$ the reference MRSI signal reconstructed from the companion metabolic imaging data. Note the parametric variations along $$$T$$$ account for the signal changes due to different flip angles and T₂ preparation pulses.
In this work, $$$d(\boldsymbol{k},t,T)$$$ samples the $$$(\boldsymbol{k},t)$$$-space very sparsely (Fig. 1b); so the inverse problem in Eq. (1) is highly under-determined. We solve this problem using a constrained signal model that effectively incorporates the spatiospectral priors in $$$\rho_{\text{ref}}(\boldsymbol{x},t)$$$.

GS-Assisted Low-Rank Tensor Model
In this work, we express $$$\rho(\boldsymbol{x},t,T)$$$ as the following low-rank tensor:
$$\hspace{-5em}\rho(\boldsymbol{x},t,T)=\rho(\boldsymbol{x},T)\rho_{\text{ref}}(\boldsymbol{x},t)\\{\hspace{2.3em}}=\sum_{q=1}^{Q}a_{q}(\boldsymbol{x})\phi_{q}(T)\rho_{\text{ref}}(\boldsymbol{x},t)\\{\hspace{15.5em}}\text{subject to }\|a_{q}(\boldsymbol{x})-\sum_{n}c_{n}e^{i2\pi{n}\Delta{\boldsymbol{k}}{\boldsymbol{x}}}\rho_{\text{ref}}(\boldsymbol{x},0)\|_2^2\leq\delta^2.\hspace{9em}(2)$$
This signal model has several key innovative features. First, it represents the temporal-parametric variations as a rank-1 subspace: $$$\rho(\boldsymbol{x},t,T)=\rho(\boldsymbol{x},t)\rho_{\text{ref}}(\boldsymbol{x},t)$$$. This is based on the fact that the spectroscopic signals collected at different $$$T$$$ share the same acquisition sequence as $$$\rho_{\text{ref}}(\boldsymbol{x},t)$$$ except for different flip angles and T₂ preparation times; as a result, they have the same evolution pattern along $$$t$$$ except for T₁/T₂-weighting. Second, the proposed model expresses the spatial-parametric variations as a rank-$$$Q$$$ subspace: $$$\rho(\boldsymbol{x},T)=\sum_{q=1}^{Q}a_{q}(\boldsymbol{x})\phi_{q}(T)$$$. This exploits the fact that $$$\{\rho(\boldsymbol{x},T)\}$$$ for different voxels, viewed as functions of $$$T$$$, are strongly correlated such that their distributions can be captured by a low-dimensional subspace. Finally, the spatial coefficient, $$$a_{q}(\boldsymbol{x})$$$, is enforced to be well approximated by a GS model: $$$\sum_{n}c_{n}e^{i2\pi{n}\Delta{\boldsymbol{k}}{\boldsymbol{x}}}\rho_{\text{ref}}(\boldsymbol{x},0)$$$.⁹ This GS model absorbs $$$\rho_{\text{ref}}(\boldsymbol{x},0)$$$ into the spatial basis functions to effectively constrain the spatial variations.
As compared to the conventional Fourier series model, the proposed low-rank tensor model has two orders of magnitude fewer parameters (1.9×10⁶ vs. 2.8×10⁸), thereby enabling high-quality image reconstruction from highly sparse data. The GS model further imposes spatial a priori constraints, providing additional performance improvement.

Constrained Image Reconstruction
With the proposed image model, image reconstruction was done by solving the following constrained optimization problem:
$$\hspace{13em}\hat{a},\hat{c}=\arg\min_{a,c}=\|d-\Omega{F}S(\Phi{a}\otimes\rho_{\text{ref}})\|_2^2+\lambda\|a-Gc\|_2^2,\hspace{9em}(3)$$
where $$$d,a,c,\rho_{\text{ref}}$$$ are the vector forms of the measured data, $$$\{a_{q}(\boldsymbol{x})\}$$$, $$$\{c_{n}\}$$$, and $$$\rho_{\text{ref}}(\boldsymbol{x},t)$$$, respectively; $$$\Omega,F,S,\Phi,G$$$ are the operators associated with $$$(\boldsymbol{k},t)$$$-space sampling, Fourier transform, sensitivity encoding, parametric basis functions, and GS model. After $$$\hat{a}$$$ was determined, the reconstructed signal $$$\hat{\rho}(\boldsymbol{x},t,T)$$$ was synthesized using Eq. (2), and T₁/T₂ maps were then estimated by fitting the relaxation models.

Results

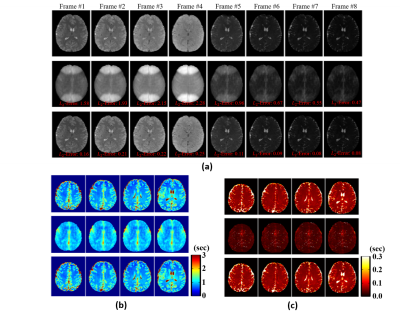
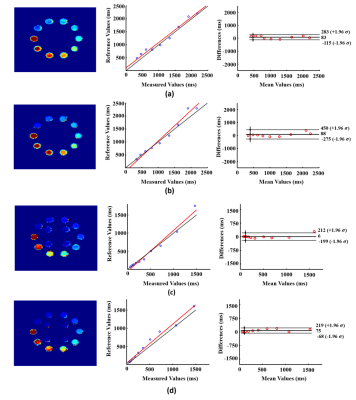
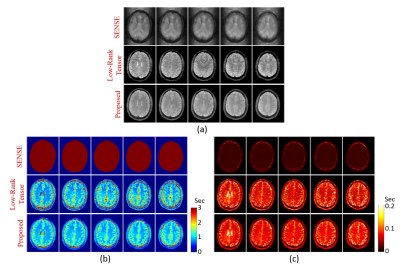
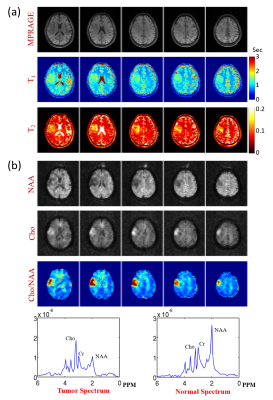
The proposed method has been evaluated using both simulated and experimental data. Simulated data were constructed based on Eq. (2) with true parameters determined from an in vivo dataset plus Gaussian noise. Experimental data were obtained from both phantom and human subjects on 3T systems (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) using the following imaging parameters: TR/TE=160/1.6ms, FOV=230×230×72mm³, matrix size=216×122×72, FA=12/17/22/27/32°, TP=0/20/40/60/80ms, scan time=8.5min. Figure 2 shows the simulation results, which compare our method with conventional SENSE reconstruction. As shown, the proposed method significantly improved the reconstruction accuracy. Figure 3 shows the phantom results, which demonstrate that our imaging method achieved comparable accuracy as standard T₁/T₂ imaging methods (VFA-FLASH¹⁰ and multi-TE-TSE¹¹). Figure 4 shows the in vivo results, where we compared SENSE-based, low-rank tensor-based (i.e., using the proposed model in Eq. (2) but without GS-based constraint), and the proposed reconstruction. As shown, the low-rank tensor model significantly reduced the aliasing artifacts over traditional model, while the GS-based constraint further improved the spatial quality. We have also tested the proposed method on one brain tumor patient. As can be seen in Fig. 5, high-quality T₁/T₂ and metabolic maps were obtained from SPICE data, characterizing the tissue abnormality within the tumor.

Conclusions

This paper presents a novel model-based method for reconstruction of T₁/T₂ maps from unsuppressed water signals acquired in MRSI scans supplemented with highly sparse T₁/T₂-encoded data. The proposed method utilizes the low-rank tensor and GS model to effectively absorb the spectral and spatial priors. Reconstructions results from both simulated and experimental data demonstrated the potential of the proposed method to support rapid simultaneous metabolic and parametric imaging.

Acknowledgements

No acknowledgement found.