Synopsis

Keywords: Quantitative Imaging, Quantitative Imaging

The 3D-quantification using an interleaved Look-Locker acquisition sequence with T₂ preparation pulse (3D-QALAS) has been developed and used for acquiring high-resolution T₁, T₂, and PD maps from five measurements within each repetition time. However, it assumes that each k-space data is acquired instantly at the first echo train length index neglecting T₁ and T₂ relaxation during the acquisition, which might cause blurring and biases in the reconstructed maps. In this study, we propose to reconstruct accurate quantitative T₁ and T₂ maps with reduced blurring compared to the conventional QALAS method using our proposed zero-shot deep subspace reconstruction method (i.e., Zero-DeepSub).

Introduction

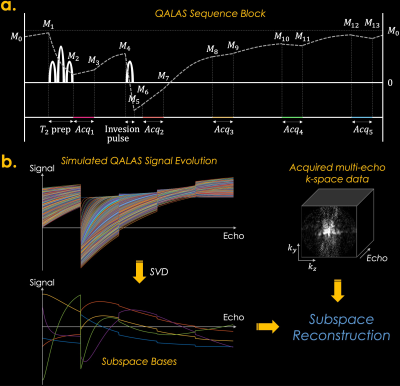
Low-rank subspace/shuffling methods have been powerful for reconstructing time-resolved MRI data and quantitative MRI (qMRI) since they incorporate subspace bases that are calculated from Bloch equations^1-3. The 3D-quantification using an interleaved Look-Locker acquisition sequence with T₂ preparation pulse (3D-QALAS) has been developed and used for acquiring high-resolution T₁, T₂, and PD maps from five measurements within each repetition time (TR)^4-6. However, when fitting the quantitative maps using a Bloch-simulated dictionary, it assumes that each k-space data is acquired instantly at the first echo of the lengthy echo train, thus neglecting T₁ and T₂ relaxation during the acquisition, which might cause blurring and biases in the reconstructed T₁ and T₂ maps. Thus, in this study, we propose to reconstruct QALAS time-series data using a low-rank subspace method and enable more accurate T₁ and T₂ mapping with reduced blurring compared to the conventional QALAS method. The overall scheme is presented in Fig. 1. Furthermore, we propose a novel zero-shot deep-learning subspace method (i.e., Zero-DeepSub), which combines a scan-specific deep-learning-based reconstruction method^7-9 with a low-rank subspace, to further improve the fidelity of multiparametric quantitative MRI.

Example Code: https://anonymous.4open.science/r/Zero-DeepSub/

Methods & Experiments

Problem Formulation:
Subspace reconstruction can be formulated as follows:
$$\begin{aligned}\underset{\mathbf{x}}{\operatorname{min}}\left\|\mathbf{y}-\mathbf{Ax}\right\|^2_2+\lambda\cal{R}\mathrm{(}\mathbf{x}\mathrm{)}\,,&&(1)\end{aligned}$$
with
$$\begin{aligned}\mathbf{A}=\mathbf{MFC{\Phi}}:\mathbb{C}^{N\times{K}}\to\mathbb{C}^{N\times{C}\times{T}}\,,&&(2)\end{aligned}$$
where $$$\mathbf{y}$$$ denotes the acquired multi-echo and multi-coil k-space data, $$$\mathbf{x}$$$ the denotes the desired subspace coefficient images, and $$$\mathbf{A}$$$ denotes the forward operator that has a k-space sampling matrix $$$\mathbf{M}$$$, Fourier transform $$$\mathbf{F}$$$, coil sensitivity map $$$\mathbf{C}$$$, and subspace bases $$$\mathbf{\Phi}$$$, which transforms the subspace coefficients ($$$\mathbb{C}^{N\times{K}}$$$) into multi-echo and multi-coil k-space data ($$$\mathbb{C}^{N\times{C}\times{T}}$$$). $$$N$$$, $$$K$$$, $$$C$$$, and $$$T$$$ denote the matrix size of the image, number of bases, coils, and echoes. $$$\cal{R\mathrm{(}\cdot\mathrm{)}}$$$ denotes the regularization term and $$$\lambda$$$ denotes the regularization parameter. The l₁-wavelet-based regularization is generally used for a subspace reconstruction.

Proposed Model: We propose to use a zero-shot self-supervised learning scheme⁸ for subspace reconstruction where Eq. 1 with the deep-learning-based regularization¹⁰ can be represented as follows:
$$\begin{aligned}\underset{\mathbf{x}}{\operatorname{min}}\left\|\mathbf{y}-\mathbf{MFC{\Phi}x}\right\|^2_2+\lambda\left\|\mathbf{x}-\mathbf{\mathcal{D\mathrm{(}\mathbf{x};\boldsymbol{\theta}\mathrm{)}}}\right\|^2_2\,,&&(3)\end{aligned}$$
where $$$\mathcal{D}$$$ is the convolutional neural network (CNN)-based denoiser with trainable parameters $$$\boldsymbol{\theta}$$$, which can be optimized by minimizing the training loss $$$\mathcal{L_{train}}$$$:
$$\begin{aligned}\underset{\mathbf{\boldsymbol{\theta}}}{\operatorname{min}}\sum_{p=1}^{P}\mathcal{L_{train}}\Big({\mathbf{y}}_{\mathrm{\Lambda}_{p}},\:{\mathbf{A}}_{\mathrm{\Lambda}_{p}}\cal{H}\mathrm{(}{\mathbf{y}}_{\mathrm{\Theta}_{p}},{\mathbf{A}}_{\mathrm{\Theta}_{p}};{\boldsymbol{\theta}}\mathrm{)}\Big)\,,&&(4)\end{aligned}$$
and optimal parameters $$$\boldsymbol{\theta}$$$ can be determined by observing the validation loss $$$\mathcal{L_{val}}$$$:
$$\begin{aligned}\mathcal{L_{val}}\Big({\mathbf{y}}_{\mathrm{\Gamma}},\:{\mathbf{A}}_{\mathrm{\Gamma}}\cal{H}\mathrm{(}{\mathbf{y}}_{\mathrm{\Omega\backslash\Gamma}},{\mathbf{A}}_{\mathrm{\Omega\backslash\Gamma}};{\boldsymbol{\theta}_p}\mathrm{)}\Big)\,,&&(5)\end{aligned}$$
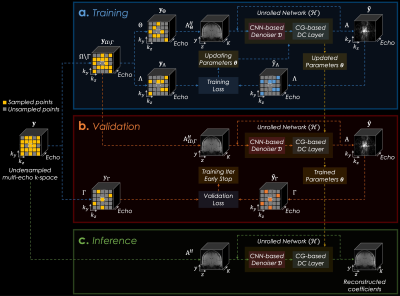
where $$$\cal{H}\mathrm{(}{\mathbf{y}}_{\mathrm{(\cdot)}},{\mathbf{A}}_{\mathrm{(\cdot)}};{\boldsymbol{\theta}_{\mathrm{(\cdot)}}}\mathrm{)}$$$ is the function of the unrolled network using the k-space data $$$\mathbf{y}_{\mathrm{(\cdot)}}$$$, forward model $$$\mathbf{A}_{\mathrm{(\cdot)}}$$$, and trainable parameters $$$\boldsymbol{\theta}_{\mathrm{(\cdot)}}$$$. Here, a k-space sampling strategy is used, which splits the original k-space sampling mask into three different subsets without overlap (i.e., $$$\Omega=\Theta\sqcup\Lambda\sqcup\Gamma$$$) for model training $$$\Theta$$$, training loss $$$\Lambda$$$, and validation loss $$$\Gamma$$$ in each epoch $$$p$$$ ($$$p=1,...,P$$$). The detailed architecture of our proposed model is presented in Fig. 2.

Implementation Details: The CNN-based denoiser consists of 5 layers where each layer has a 3x3 convolutional layer with 128 channels and a leaky ReLU activation with 0.05 negative slope coefficient. The trainable parameter $$$\lambda$$$ was initialized as 0.05. We used conjugate gradients for a data consistency layer with 10 iterations. A total of 4 iterations were performed in the unrolled network. A loss function $$$\cal{L}$$$ was defined as the summation of l₁ and l₂ norm of the difference between the reconstructed and acquired k-space, which were multiplied with the calculated sampling mask. We made different subsets of sampling masks in each epoch without pre-determined ones using $$$\left|\Omega\right|/\left|\Gamma\right|$$$=0.2 and $$$\left|\Lambda\right|/\left|{\Omega\backslash\Gamma}\right|$$$=0.4. The model was trained with Adam and implemented using Tensorflow.

Acquisition and Simulation: We acquired data from a volunteer using 3D-QALAS sequence on a 3T Prisma scanner with a 32ch head receive array. The parameters are as follows: FOV=240x240x202mm³, matrix size=206x206x176, BW=330Hz/pixel, echo-spacing=5.76ms, turbo factor=128, TR=4.5s, TE=2.29ms, acceleration R=2, and scan time=8m 24s. We retrospectively conducted undersampling with R=2x5 for further validation. For the simulation, we also generated the k-space data using QALAS Bloch-simulation with the same scan parameters.

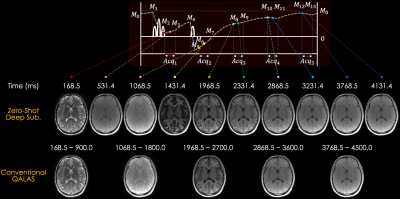
Experiments: We evaluated our proposed Zero-DeepSub by comparing it with 1) conventional QALAS that fits the T₁ and T₂ maps using original five measurements, 2) subspace reconstruction without regularization, and 3) subspace reconstruction with l₁-wavelet regularization. The dictionary was generated with the following T₁, and T₂ ranges: T₁=[300–5000ms] and T₂=[10–500ms]. We used 4 bases that could generate the simulated signals within 1.25% errors. The sequence diagram of QALAS is presented in Fig. 1b. We used BART toolbox for estimating coil sensitivity maps and comparison subspace methods¹¹.

Results

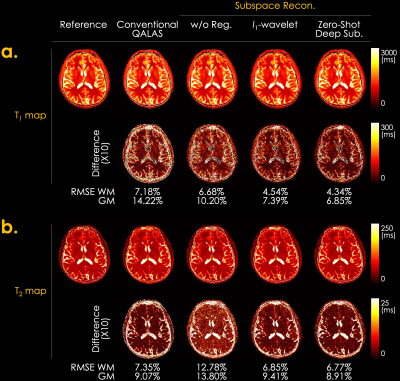
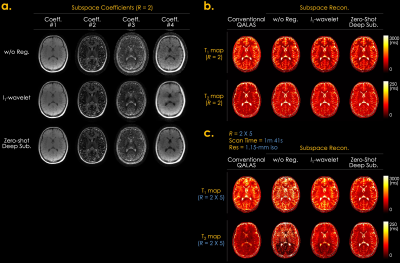
Fig. 3 shows the simulation results of T₁ and T₂ maps reconstructed using the conventional QALAS and subspace methods without regularization, l₁-wavelet regularization, and proposed Zero-DeepSub. The proposed method shows reduced T₁ and T₂ biases compared to other methods as quantified by root mean squared error (RMSE) of white and gray matter. Fig. 4 presents in vivo subspace coefficients and T₁ and T₂ maps reconstructed using three different subspace methods. The proposed method shows noise-reduced and sharper coefficients, especially for the third and fourth ones, which result in better T₁ and T₂ maps. Furthermore, we can resolve interim images within each acquisition with virtual inversion times (TIs) while conventional QALAS only has five reconstructed volumes (Fig. 5).

Discussion & Conclusion

In this study, we demonstrated that accurate T₁ and T₂ maps with reduced blurring can be obtained using the proposed Zero-DeepSub, which combines scan-specific deep-learning reconstruction with low-rank subspace, from 3D-QALAS measurements.

Acknowledgements

This work was supported by research grants NIH R01 EB032378, R01 EB028797, R03 EB031175, U01 EB025162, P41 EB030006, U01 EB026996, and the NVidia Corporation for computing support.