Synopsis

Keywords: Quantitative Imaging, Data Acquisition

We demonstrate a new extension of Selective Encoding through Nutation and Fingerprinting (SENF) which is a RF spatial encoding technique that also encodes quantitative information. This SENF method uses quadratic RF phase modulation sequence with an off-resonant Bloch-Siegert pulse to induce the Bloch-Siegert shift to simultaneously encode spatial and quantitative information. We validate this method on a 47.5mT low-field scanner and in simulation.

Introduction

Conventional MRI uses B₀ gradients for spatial encoding, which are expensive, bulky, noisy, prone to breakage, and induce PNS. Several spatial encoding methods have been proposed that use RF gradients^1-4 instead of B₀ gradients, but none enable quantitative imaging of T₁ and T₂ relaxation times. Selective Encoding through Nutation and Fingerprinting (SENF)^5,6, can accomplish RF spatial encoding and quantitative imaging simultaneously using MR Fingerprinting⁷-like sequences that encode space as additional dimensions. Here we describe a SENF method that uses quadratic RF phase modulation sequence^8,9 which enables resonance frequency and relaxation mapping simultaneously. Off-resonant Bloch-Siegert pulses transmitted through a RF gradient coil induce the Bloch-Siegert shift to map the resonance frequency to B₁ (Figure 1). The known B₁ map of the RF gradient coil allows us to map B₁ to space. We validate this method on a 47.5mT low-field scanner and in simulation.

Methods

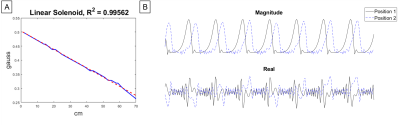
A linear solenoid with r=6cm and L=20cm was constructed with a uniform saddle coil with r=1.75cm and L=12cm on a coil holder positioning it in the center of the solenoid (Figure 3). The coils were geometrically decoupled by 30dB and a further 40dB with a Reed relay TR switch. The phantom holder was used for positioning a 2.5cm ball phantom of mineral oil (T₁=104ms, T₂=96ms). The setup was placed in a shielded box to reduce EMI. The experiments were performed on a 47.5mT low-field scanner.

The linear solenoid allows us to map B₁ to space with a known B₁ map (Figure 1A). An off-resonance Bloch-Seigert pulse is applied after each excitation in the pulse sequence to produce a resonance frequency shift and consequently a phase shift across the FOV that is proportional to B₁ according to the Bloch-Siegert shift. Using quadratically incremented phase and constant flip excitation pulses we are able to encode the resonance frequency in the signal time courses (Figure 1B).

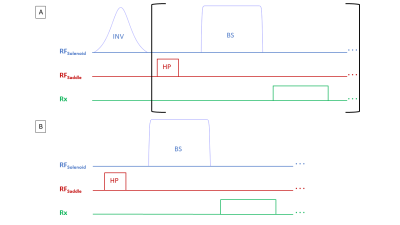
The pulse sequence (Figure 2B) consists of a series of hard pulse excitations with a constant flip angle of 10° with a quadratically incremented phase updated at each TR. The hard pulses were transmitted through the saddle coil and immediately followed by an 10kHz off-resonance 9ms Bloch-Seigert pulse that was transmitted through the linear solenoid to produce a resonance frequency shift that resulted in a 2π phase shift across the FOV. The sequence consisted of N=250 TRs 20ms each in length and a 1 second delay between the 16 averages taken for a total scan time of 96 seconds.

For the experiment a mineral oil phantom was placed in the phantom holder and slid through the 8cm FOV in 0.5cm steps and data were collected at each location. A Bloch simulation was used to simulate signal time courses across B₁ amplitudes for an 8cm FOV for mineral oil at a spatial resolution of 1mm. These signal time courses were used to populate a dictionary and the collected data were reconstructed with a regularized pseudo inverse.

Additionally we simulated an experiment with mineral oil and doped water balls (T₁=330ms, T₂=220ms). An inversion pulse was added and the flip angle of the excitation pulses was increased to 50° to improve encoding of T₁ and T₂ (Figure 2A). A Bloch simulation was used to simulate signal time courses across B₁ for an 8cm FOV for mineral oil and dope water at a spatial resolution of 1mm. Signal time courses for the data were constructed from the dictionary by taking a weighted sum across entries using the expected ball phantom positions and adding Gaussian noise to each data set (SNR= 50). The data were constructed for mineral oil and doped water phantoms placed adjacent to each other and slid through the FOV. If a ball phantom would be outside the FOV it was removed. The data were then reconstructed with a regularized pseudo inverse.

Results

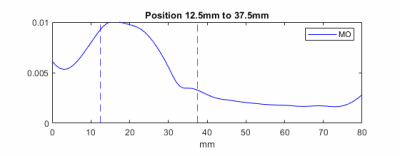
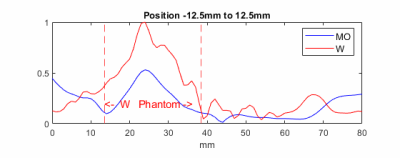
The 1mm resolution reconstructions for the mineral oil experiment match the expected positions (Figure 4), demonstrating that SENF can resolve objects both spatially and through relaxation differences. The peaks may be broadened due to the B₀ distribution within the ball phantoms due to inhomogeneity of the magnet. The amplitude of the reconstruction coefficients remain consistent for different positions implying that they reflect spin density.

The simulated mineral oil and doped water reconstructions show the coefficients match the expected ball positions. The coefficients are also higher for the correct T₁ and T₂ at each position showing they were encoded sufficiently (Figure 5).

Discussion

The presented experimental/simulated results validate this novel embodiment of the SENF concept for 1mm 1D reconstructions of two materials on a 47.5mT low-field scanner. We have shown that spatial and quantitative encoding of these NMR signals can be done without B₀ gradients using SENF. This method could enable decoupling of spatial encoding from the T₁ and T₂ encoding dimensions for independent optimization of spatial and quantitative resolution. We will further integrate low cost on-board RF power amplifiers^10,11 and a parallel transmit array to perform these experiments in 2D. Finally, we will extend this method with B1+-Selective excitations^12,13.

Acknowledgements

This work was supported by NIH grant R01 EB 032709.