1083
Free-running 3D-CINE MRI of patients with congenital heart disease using inter-bin compensation of cardiac motion
Bastien Milani1, Christopher Roy1, Jean-Baptist Ledoux1, David C. Rotzinger1, Salim Si-mohamed1,2,3, Ambra Masi1, Jerome Yerly1,4, Tobias Rutz1, Milan Prsa1, Jurg Schwitter1, and Matthias Stuber1,4
1Lausanne University Hospital (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 2INSA-Lyon, CNRS, Inserm, CREATIS, Université de Lyon,, Villeurbanne, France, 3Louis Pradel Hospital, Hospices Civils de Lyon, Bron, France, 4Center for Biomedical Imaging (CIBM), Lausanne, Switzerland
1Lausanne University Hospital (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 2INSA-Lyon, CNRS, Inserm, CREATIS, Université de Lyon,, Villeurbanne, France, 3Louis Pradel Hospital, Hospices Civils de Lyon, Bron, France, 4Center for Biomedical Imaging (CIBM), Lausanne, Switzerland
Synopsis
Keywords: Heart, Cardiovascular, ejection fraction
We present in this work a 3D-CINE whole-heart reconstruction that we developed for free-running 3D‑radial fully self-gated acquisitions. The reconstruction is compressed-sensing-based with temporal-total-variation (tTV) regularization, which is known to corrupt or compress motion and to blur moving structures. In order to solve these drawbacks, we regularize by an improved tTV equal to the one-norm of the sum of the motion-corrected-residuals between adjacent frames. While this strategy has already been applied for various trajectories, it has never been applied for 3D-radial in free-running. In this study, we demonstrate quantitatively and qualitatively that this strategy in fact improves image quality.Background
Cardiac motion-resolved images acquired with 3D-radial free-running MRI sequences promote a high degree of sparsity in the difference between adjacent frames, that lends itself to compressed-sensing (CS) with temporal-total-variation (tTV) regularization. In order to solve motion-related problems inherent to tTV regularization, such as movement compression and blurring of structures, CS-reconstruction including deformation-fields in the tTV-regularization term have been implemented [1]–[6], [7], [8]. However, untapped potential remains in that it has not been exploited for 3D-radial free running data. We implemented such a solution and tested the hypothesis that image quality can thus be further improved. Moreover, we show that the ejection fraction (EF) can be accurately measured on our reconstructed images.Methods
Fully self-gated data were acquired with a 3D-radial free-running gradient echo sequence after injection of 2mg/kg dose of ferumoxitol contrast medium in 12 congenital heart disease patients (age = 22±9 years). Informed consent was obtained from all individuals or representatives. Data were binned into motion-consistent sets of lines in k-space [9], called bins, to resolve respiratory and cardiac motion. Only the end-expiratory bin was used in order to resolve respiratory motion. The cardiac bins were then used to reconstruct 3D-CINE images. A first reconstruction (recon-nonDF_01) without use of DF but with regularization along the cardiac dimension ( λ=0.1, optimized empirically on one dataset) was performed by solvingargminx ½∑i=1:nFR ||F(i)C x(i) - y(i)||22 - λ/2 ||T(i)x(i) - x(i-1)||1
where index i runs over the frames, nFR is the total number of frames, x is the image, x(i) stands for the i-th frame, C for coil-sensitivity, F(i) for non-uniform Fourier transform, y(i) for the raw-data vector of i-th frame and each T(i) was set equal to identity. It was assumed that x(0)=x(nFR) in a circular fashion. Note that the name "recon-nonDF_01" referse to λ=0.1.
Motion between adjacent frames was then estimated using non-rigid registration [10]. A second reconstruction (recon-DF_03, λ=0.3) including DF was performed by setting each T(i) equal to the linear map that deforms frame x(i) into x(i-1) by utilizing the previously estimated DF. Another reconstruction (recon_nonDF_03, λ=0.3) without DF was then performed in order to decouple the effects of regularization weights from the inclusion/exclusion of DF. Quantitative end-points were compared between recon-nonDF_01 and recon-DF_03 in mid-diastole (when movement is the slowest) including sharpness of RCA, LAD [11] and blood-myocardium interface sharpness [12]. A region in the blood pool with homogeneous signal was selected and the spatial-total-variation (sTV), as well as the average signal divided by its standard deviation, were extracted as surrogate end-points for signal-to-noise ratio. A blinded experienced radiologist (DR) performed qualitative comparison based on the following comparison criteria: Sharpness of aortic branch vessels interface, aortic valve leaflets, LCA, LAD, LCx and RCA, perceived noise, and overall diagnostic confidence. EF was quantified by a threshold-segmentation of left-ventricle on end-diastolic and end-systolic images from recon-DF_03 and the result was compared to the standard EF as obtained by conventional 2D-CINE acquisition. Analysis was performed by a blinded reader with CMR analysis experience (AM). Ejection fractions were rounded to the closest integer for consistent comparison with those from cardiology reports. The significance of the average-difference between any two lists of values was assessed by a two-tailed t-test.
Results
As compared to recon-nonDF_01, Recon-DF_03 led to a 6.0%±5.2% improvement in RCA sharpness (p<0.01), to a 3.8%±3.8% improvement for that of the LAD (p<0.01) and the blood-myocardium interface sharpness improvement amounted of 24.5%±23.8% (p<0.01). In a homogeneous region of the blood pool, the ratio average/standard-deviation was improved by 8.8%±4.8% (p<0.01) for recon_DF_03 and the spatial total variation was reduced by 12.6%±7.9% (p<0.01). Table 1 shows the results of the blinded qualitative analysis performed by the radiologist. It corroborates the quantitative analyses where the majority of anatomical features where better visualized using recon_DF_03. Figure 2 is consistent with these findings and a comparison between recon-nonDF_01 (left column), recon-nonDF_03 (middle column) and recon-DF_03 (right column) is provided. Figures 3 shows the same for an other patient. In Figure 4, a reformat of the right coronary artery obtained from recon_nonDF_01 (figure 4A), recon_nonDF_03 (figure 4B), and recon_DF_03 (figure 4C) is displayed. Figure 4D, 4E and 4F visualize the same type of reformats obtained from a different time-point in the cardiac cycle. The EF was evaluated in 8 of the 12 patients because 4 had a single-ventricle physiology after Fontan reconstruction of a single ventricle pathology. The measured EF in recon-DF_03 and conventional 2D-CINE were not significantly different and their averaged difference was smaller than 1%. Figure 5A shows EF measured on recon-DF_03 versus EF measured on conventional 2D-CINE while figure 5B shows EF measured on conventional 2D-CINE by one observer versus another observer for comparison.Conclusion
By incorporating frame-to-frame deformation fields into the compressed sensing reconstruction, anatomical structures become more conspicuous, which is supported by both quantitative and qualitative findings. This enables the use of a higher temporal regularization without additional blurring, which advances the hypothesis that reconstruction informed by DF may also be exploited to abbreviate scanning times. We also show that the ejection fraction, one of the most critical values for clinical decision making, can be accurately measured on fully self-gated 3D-radial free-running images.Acknowledgements
No acknowledgement found.References
[1] S. G. Lingala, E. DiBella, et M. Jacob, « Deformation Corrected Compressed Sensing (DC-CS): A Novel Framework for Accelerated Dynamic MRI », IEEE Trans. Med. Imaging, vol. 34, no 1, p. 72‑85, janv. 2015, doi: 10.1109/TMI.2014.2343953. [2] M. S. Asif, L. Hamilton, M. Brummer, et J. Romberg, « Motion-adaptive spatio-temporal regularization for accelerated dynamic MRI », Magn. Reson. Med., vol. 70, no 3, p. 800‑812, sept. 2013, doi: 10.1002/mrm.24524. [3] N. Zhao, D. O’Connor, A. Basarab, D. Ruan, et K. Sheng, « Motion Compensated Dynamic MRI Reconstruction With Local Affine Optical Flow Estimation », IEEE Trans. Biomed. Eng., vol. 66, no 11, p. 3050‑3059, nov. 2019, doi: 10.1109/TBME.2019.2900037. [4] J. Royuela-del-Val, L. Cordero-Grande, F. Simmross-Wattenberg, M. Martín-Fernández, et C. Alberola-López, « Jacobian weighted temporal total variation for motion compensated compressed sensing reconstruction of dynamic MRI: Jacobian Weighted temporal Total Variation », Magn. Reson. Med., vol. 77, no 3, p. 1208‑1215, mars 2017, doi: 10.1002/mrm.26198. [5] R.-M. Menchón-Lara et al., « An Efficient Multi-resolution Reconstruction Scheme with Motion Compensation for 5D Free-Breathing Whole-Heart MRI », in Molecular Imaging, Reconstruction and Analysis of Moving Body Organs, and Stroke Imaging and Treatment, vol. 10555, M. J. Cardoso, T. Arbel, F. Gao, B. Kainz, T. van Walsum, K. Shi, K. K. Bhatia, R. Peter, T. Vercauteren, M. Reyes, A. Dalca, R. Wiest, W. Niessen, et B. J. Emmer, Éd. Cham: Springer International Publishing, 2017, p. 136‑145. doi: 10.1007/978-3-319-67564-0_14. [6] J. Royuela-del-Val, L. Cordero-Grande, F. Simmross-Wattenberg, M. Martín-Fernández, et C. Alberola-López, « Nonrigid groupwise registration for motion estimation and compensation in compressed sensing reconstruction of breath-hold cardiac cine MRI: Groupwise ME/MC in CS Reconstruction of Cardiac Cine MRI », Magn. Reson. Med., vol. 75, no 4, p. 1525‑1536, avr. 2016, doi: 10.1002/mrm.25733. [7] S. Sridi et al., « Improved myocardial scar visualization with fast free-breathing motion-compensated black-blood T1-rho-prepared late gadolinium enhancement MRI », Diagnostic and Interventional Imaging, p. S2211568422001425, août 2022, doi: 10.1016/j.diii.2022.07.003. [8] A. Bustin et al., « 3D whole-heart isotropic sub-millimeter resolution coronary magnetic resonance angiography with non-rigid motion-compensated PROST », J Cardiovasc Magn Reson, vol. 22, no 1, p. 24, déc. 2020, doi: 10.1186/s12968-020-00611-5. [9] L. Di Sopra, D. Piccini, S. Coppo, M. Stuber, et J. Yerly, « An automated approach to fully self‐gated free‐running cardiac and respiratory motion‐resolved 5D whole‐heart MRI », Magn Reson Med, vol. 82, no 6, p. 2118‑2132, déc. 2019, doi: 10.1002/mrm.27898. [10] M. Modat et al., « Fast free-form deformation using graphics processing units », Computer Methods and Programs in Biomedicine, vol. 98, no 3, p. 278‑284, juin 2010, doi: 10.1016/j.cmpb.2009.09.002. [11] A. Etienne, R. M. Botnar, A. M. C. van Muiswinkel, P. Boesiger, W. J. Manning, et M. Stuber, « “Soap-Bubble” visualization and quantitative analysis of 3D coronary magnetic resonance angiograms », Magn. Reson. Med., vol. 48, no 4, p. 658‑666, oct. 2002, doi: 10.1002/mrm.10253. [12] R. Ahmad, Y. Ding, et O. P. Simonetti, « Edge sharpness assessment by parametric modeling: Application to magnetic resonance imaging: EDGE SHARPNESS ASSESSMENT FOR MRI », Concepts Magn. Reson., vol. 44, no 3, p. 138‑149, mai 2015, doi: 10.1002/cmr.a.21339.Figures
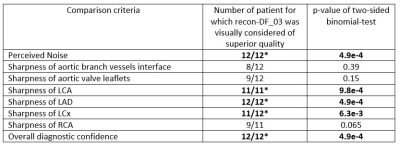
Table 1: Blinded qualitative analysis by a radiologist.
The left column describes the comparison criteria. The middle column counts the
number of patients were recon-DF_03 was preferred according to the criteria given
on the left and the right column shows the p-values according to a two-sided
binomial test.
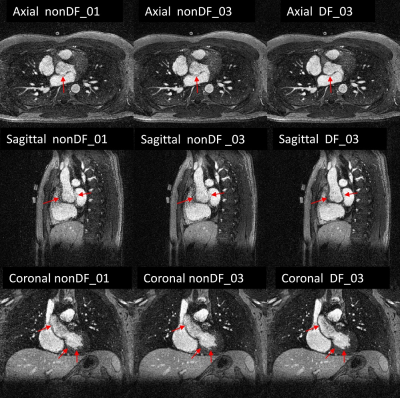
Figure 2: 3D-CINE frame displayed in 3 orientations. The images in the left column were obtained
from recon-nonDF_01, those from the middle column from recon-nonDF_03, and
those in the right column from recon-DF_03.
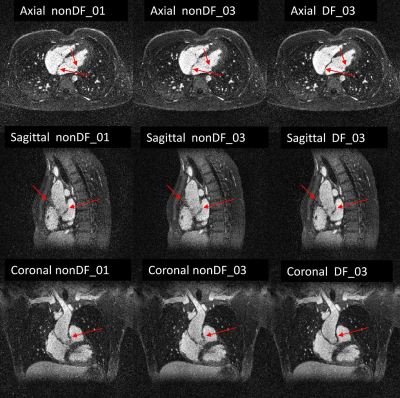
Figure 3: 3D-CINE frame displayed in 3 orientations. The images in the left column were
obtained from recon-nonDF_01, those from the middle column from recon-nonDF_03,
and those in the right column from recon-DF_03.
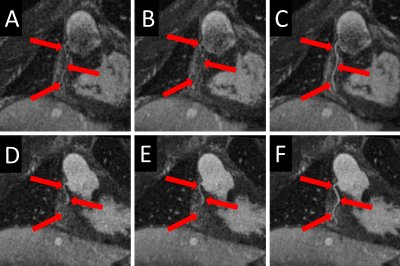
Figure 4 : Each
of the subfigures displays a SoapBubble-reformatted image of the right coronary
artery from the same volunteer. Top row (A, B, C) and bottom row (D, E, F) correspond
to two different time points. The images in the left column (A and D) were obtained
from recon-nonDF_01, those in the middle column (B and E) from recon-nonDF_03,
and those in the right column (C and D) from recon-DF_03.
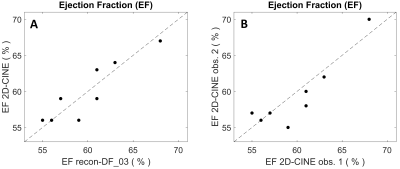
Figure 5:
Subfigure A displays the ejection-fraction measured from recon-DF_03 acquired with
fully self-gated 3D-radial free-running MRI versus conventional 2D-CINE imaging.
Subfigure B shows conventional 2D-CINE EF measurements from two different observers.
DOI: https://doi.org/10.58530/2023/1083