Synopsis

Keywords: Susceptibility, Quantitative Susceptibility mapping

Acquisition of whole brain Quantitative Susceptibility Mapping (QSM) is time-consuming that requires the patient’s effort. On the other hand, limiting the QSM field-of-view to only the region of interest (e.g., deep grey matter) can shorten scan time and lessen the patient’s burden. However, reducing spatial coverage degrades conventional background field removal performance, resulting in an underestimation of susceptibility values. To overcome these limitations, we propose a harmonic field extension method using a physics-informed generative adversarial network. According to the experimental results, the proposed method significantly improves the accuracy of both the local field and QSM at reduced spatial coverage.

Introduction

Quantitative Susceptibility Mapping (QSM), which can estimate the spatial distribution of magnetic susceptibility in brain tissues is widely used in the study of brain iron related to brain development and diseases in deep gray matter(DGM)¹. However the acquisition of whole-brain QSM is time-consuming. On the other hand, obtaining QSM only over the region of the interest such as DGM by reducing field-of-view (FOV) can shorten scan time and enable to enhance the spatial resolution without increasing scan time^2,3. However severe susceptibility value underestimation has been reported during QSM reconstruction with limited FOV especially due to the incorrect background field removal by boundary field cut-off. Therefore, there are still many limitations to the clinical use of QSM with small spatial coverages reconstructed only by conventional methods.
To correct errors propagated during the reconstruction process, we propose harmonic field extrapolation method based on physics-informed generative adversarial network. Through our method, which improves the background field removal performance in limited FOV, the susceptibility underestimation issue of QSM with small spatial coverage can be overcome.

Method

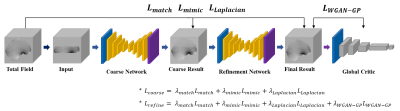
A total of 6 subject’s local fields were used in the multi-orientation gradient-echo in-vivo MRI dataset⁴. Background fields were generated through forward calculation of geometric susceptibility sources randomly placed outside the brain ROI. Total fields used for training input were generated by adding the background field to the local field. Finally, total fields were truncated along the z-axis to a minimal extent containing deep gray matter with masks and randomly cropped into 64x64x64 sized 3D patches for network training.
The network architecture follows the structure of a 3D coarse-to-fine generative model⁵ as shown in Figure 1. First, the coarse network takes the masked total field and generates a coarse prediction of the background field. Then, the refinement network takes the coarse prediction and produces the final prediction of the background field. Intuitively, the refinement network can see a more complete field than the original image with missing regions. Therefore, this two-stage framework allows the refinement network to learn a better feature representation than using a single coarse network.
Since the background field is harmonic within the ROI, we added physical loss following the Laplace’s equation to further ensure that the generated field is harmonic:
$$\triangledown^{2}H_{bkg}=0,\ within\ Ω$$Where $$$\triangledown^{2}$$$ is Laplacian operator and $$$Ω$$$ is brain ROI. Since the discrete Laplacian can be calculated via convolution with a kernel, so the physical loss can be implemented by the Fourier convolution theorem⁶.
$$L_{Laplacian}\ :\ \parallel FT^{-1}\left\{FT((1-m)\cdot\ x ̃)\cdot FT(k)\right\}\parallel_{2}$$ where $$$m$$$ is the binary mask with limited FOV, $$$x ̃$$$ is generated field and $$$k$$$ is Laplacian kernel. Finally, the coarse network is trained with the physical loss $$$L_{Laplacian}$$$ and reconstruction loss $$$L_{match}$$$, $$$L_{mimic}$$$ as follows:
$$L_{match}\ :\ \parallel x_{0} \cdot m - x ̃ \cdot m\ \parallel_{1}$$$$L_{mimic}\ :\ \parallel x\cdot (1-m) - x ̃ \cdot (1-m)\ \parallel_{1}$$ where $$$x_{0}$$$ is input field and $$$x$$$ is ground-truth full image. The refinement network takes adversarial loss $$$L_{WGAN-GP}$$$⁷ additionally from global critic network which tells us the Wasserstein-1 distance between the original and the generated harmonic field.
The evaluation of the network results was performed on both 3D Shepp-Logan digital phantom and in-vivo datasets. The final network output was evaluated with the local field via conventional background field removal processes RESHARP⁸ and V-SHARP⁹ and corresponding QSM via iLSQR¹⁰.

Result

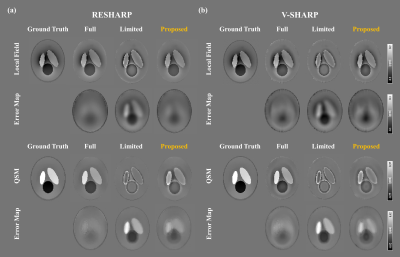
Figure 2 shows the harmonic background field extension results. The network achieves to extend the field almost perfectly. When considering the physical loss, the network further enhances smoothness compared to not using physical loss.
Figure 3 shows the feasibility of the proposed method in reduced spatial coverage through 3D Shepp-Logan digital phantom. Compared with full coverage, results with reduced coverage shows severe background field removal degradation and susceptibility underestimation. However, the proposed method enhances background field performance and overcomes the susceptibility underestimation.
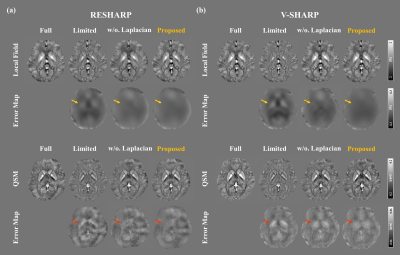
Figure 4 shows local field results and the corresponding QSM results on in-vivo test data. In-vivo results show that the extended harmonic field improves background field removal performance and corrects the susceptibility underestimation, especially in the high susceptibility regions (e.g., DGM) at reduced spatial coverage. In addition, both results are further improved when the physical loss is embedded.
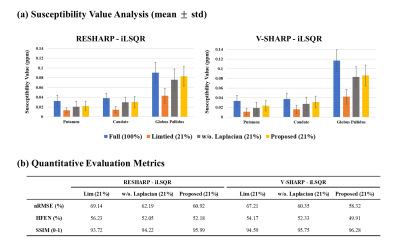
Figure 5a shows the mean susceptibility value of each DGM structure. The result shows that the QSM with reduced spatial coverage significantly underestimated the susceptibility values compared to the full, whereas the proposed method shows similar values in QSM with full spatial coverage. Figure 5b demonstrates that quantitative metric values of QSM using the proposed method are superior to those of QSM with limited FOV.

Discussion & Conclusion

In this study, we proposed physics-informed network based harmonic field extension for QSM with limited FOV. Since the network provides additional boundary field information and increases spatial coverage, it can successfully correct the underestimation of QSM with reduced FOV by improving background field removal performance. For now the focus is only on DGM, but it can be used in any field of interest, making it a powerful tool for clinical research.
Future studies will investigate the data obtained with limited FOV during actual acquisition. Comparisons with the different polynomial harmonic field extension methods such as Taylor expansion should also be conducted.

Acknowledgements

This research was supported by the MSIT(Ministry of Science and ICT), Korea, under the ITRC(Information Technology Research Center) support program(IITP-2022-2020-0-01461) supervised by the IITP(Institute for Information & communications Technology Planning & Evaluation)