Synopsis

Keywords: Motion Correction, Motion Correction

The presence of fat is a challenge in diffusion-weighted EPI. Recently, chemical-shift encoded approaches found interest, as a smart way of signal averaging, doing water/fat separation and diffusion phase navigation in the reconstruction. However, the dominant signal character of fat in diffusion could actually also be exploited as an advantage by forming a shot-specific fat navigator to track and correct for macroscopic in-plane motion, combined with a model-based self-navigated water/fat decomposition. This allows to correct for both physiological and macroscopic in-plane motion effects in DWI when estimating water and fat resolved images from chemical-shift encoded multi-shot EPI data.

Introduction

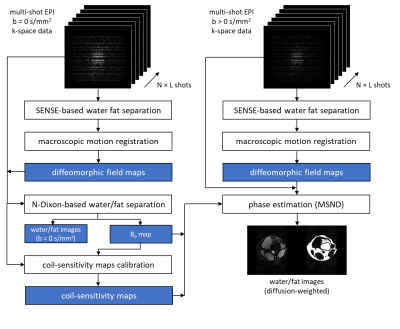
Fat is an interfering factor in EPI-based diffusion-weighted imaging (DWI) because of its chemical shift and low diffusion coefficient. To overcome shortcomings of conventional fat suppression (e.g., sensitivity to B₀ and/or B₁⁺ inhomogeneities, failure of removing the olefinic fat peak), the combination of chemical-shift encoding (Dixon-based) and DWI has become increasingly popular^1,2. Extra navigators or self-navigation is needed for each chemical-shift encoded shot, as usual in known multi-shot DWI schemes^3-5, to handle the phase changes caused by diffusion gradient induced phase-differences in presence of small physiological motion. However, macroscopic subject motion during the scan can also impair image quality, requiring further correction. Extra phase navigators could be employed for in-plane motion tracking, albeit suffering from the presence of fat signals and reduced scan efficiency². 2D fat-only navigators based on additional fat-selective excitation⁶, inspired us to follow a different route. In this work, we propose to use a SENSE-based water/fat separation⁷ to estimate a fat navigator for each shot acquisition to track and correct for macroscopic in-plane motion-induced data misalignment. This was combined with a model-based self-navigated water/fat decomposition (MSND) algorithm⁸ to jointly correct both physiological and macroscopic in-plane motion artefacts and to estimate water/fat images from chemical-shift encoded multi-shot EPI data.

Methods

To estimate water/fat images $$$x=\left[\rho_w,\rho_f\right]^T$$$of a given b-value, a minimization problem can be set up as:$$\left\{\rho_w,\rho_f\right\}^*=\underset{\rho_w,\rho_f\in\mathbb{C}^Q}{\operatorname{argmin}}\|Ax-s\|_2^2,\qquad(1)$$ where $$$s$$$ is the measured multi-shot EPI k-space data with N Dixon points, L shots and J coils. $$$A$$$ is the system matrix that can be expressed as:$$A x=K\left[\begin{array}{ll}I&I\end{array}\right]\left[\begin{array}{cc}F&0\\0&\Psi_f F\end{array}\right]\left[\begin{array}{cc}C&0\\0&C\end{array}\right]\left[\begin{array}{cc}\Psi_B&0\\0&\Psi_B\end{array}\right]\left[\begin{array}{cc}\Phi&0\\0&\Phi\end{array}\right]\left[\begin{array}{cc}M&0\\0&M\end{array}\right]\left[\begin{array}{c}\rho_w\\\rho_f\end{array}\right],\qquad(2)$$where $$$K$$$ indicates the EPI trajectory of each shot, $$$I$$$ the identity matrix, $$$\Psi_f$$$ adds the fat off-resonance, $$$F$$$ the Fourier transform, $$$C$$$ adds coil sensitivity weighting, $$$\Psi_B$$$ adds B₀-induced phase, $$$\Phi$$$ adds physiology-induced phase and $$$M$$$ adds macroscopic motion-induced transformation. These matrices are all implemented via linear operators to support efficient computations. To obtain $$$M$$$ (2D in-plane), fat images for each shot can be used to track the motion. To generate such a fat navigator efficiently, a SENSE-based water/fat separating image reconstruction is performed for each shot by introducing the chemical-shift-induced spatial shift of fat in EPI into a conventional SENSE model⁷. In this case, each EPI shot can be seen as an individual undersampled data set for which water/fat images can be reconstructed jointly⁷. Thus, the system matrix $$$B_{n,l}$$$ of $$$n$$$-th Dixon step and $$$l$$$-th shot can be written as:$$S_{n, l}=K_{n, l}[\hat{I}\hat{I}]\left[\begin{array}{cc}\hat{F}&0\\0&\widehat{\Psi}_f F\end{array}\right]\left[\begin{array}{cc}\hat{C}&0\\0&\hat{C}\end{array}\right]\left[\begin{array}{c}\rho_{w,n,l}\\\rho_{f,n,l}\end{array}\right]=B_{n,l}x_{n,l},\qquad(3)$$where $$$\hat{I},\hat{F},\widehat{\Psi}_f,\hat{C}$$$ are similar to $$$I,F,\Psi_f,C$$$ but acting on each Dixon step/shot data (n,l). However, in such an ill-conditioned problem, a proper solution for both water/fat components can be difficult to reach. But estimating a good fat image is much easier when using proper regularization, given the sparsity of the fat signal. Therefore, the Split Bregman algorithm⁹ is used to regularize both water/fat channels as:$$\left\{\tilde{\rho}_{w,n,l},\tilde{\rho}_{f,n,l}\right\}^*=\underset{\tilde{\rho}_{w,n,l,l}\tilde{\rho}_{f,n,l}\in\mathbb{C}^Q}{\operatorname{argmin}}\left\{\frac{\mu}{2}\left\|B_{n,l}\tilde{x}_{n,l}-s\right\|_2^2+\frac{\lambda}{2}\left(\left\|\nabla_x x_{n,l}\right\|_1+\left\|\nabla_y x_{n,l}\right\|_1\right)\right\},\qquad(4)$$where $$$\nabla_{x/y}$$$are first-order differential operators. The in total reconstructed N$$$\times$$$L individual fat navigators $$$\tilde{\rho}_{f,n,l}$$$ can be used to estimate the rigid motion operators while performing registration to the reference $$$n_{0}$$$-th and $$$l_{0}$$$-th fat navigator. In this work, the diffeomorphic field-based registration¹⁰ with linear interpolation for resampling was used. This motion estimation step needs to be performed for all shots as a preprocessing step. From the non-diffusion case (b=0 s/mm²), a B₀ map was estimated by setting up a Gauss-Newton loop for Eq.2 (neglecting the diffusion phase ) to jointly estimate water/fat images and a B₀ map. The coil-sensitivity map was estimated by ESPIRiT^8,11. For the diffusion case, after the rigid motion estimation, the water/fat images using self-navigation, applied to estimate the physiological motion-induced shot-to-shot phase errors, can be calculated via the MSND algorithm⁸ as shown in Fig.1. The regularization parameters $$${\mu}/{\lambda}$$$ were chosen as 0.01/0.0005.
To test this motion correction approach, leg/knee data were acquired using a 3T-MRI (Philips, Best, Netherlands). A 4-shot (msh) chemical-shift encoded DW EPI spin-echo sequence^2,8 was applied with the following parameters: TR/TE=5000/74ms, resolution 1.5×1.5×4 mm³, three b-values (0,300,600 s/mm²), using a 16-channel knee coil. Three chemical-shift encoding steps TEs 0.2/1.0/1.8 ms relative to the spin echo were used. One volunteer’s calf and one volunteer’s knee data were acquired with the volunteers asked to move their leg slightly in-plane, in between shots, to simulate macroscopic motion-induced in-plane inconsistencies between the different shots during scanning.

Results

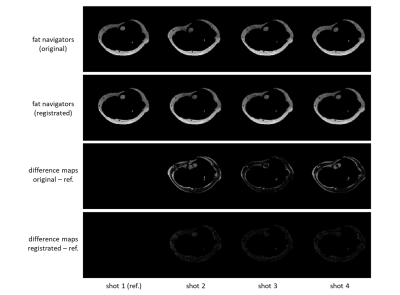
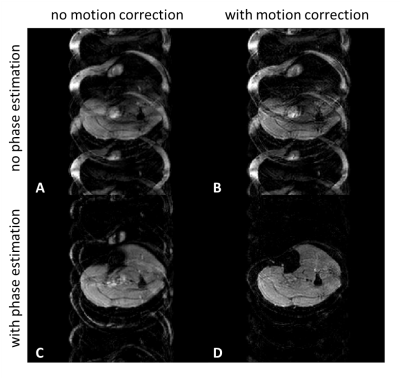
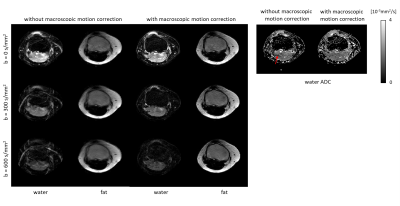
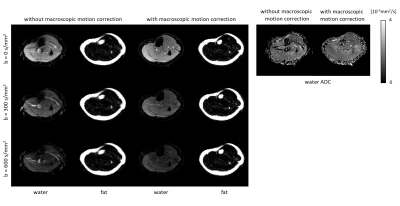
Figure 2 shows example fat navigators along with the registration performance. Figure 3 shows diffusion data reconstructed with/without phase estimation (corrected for physiological motion) and with/without macroscopic motion correction. With both options active, an artefact-free water image can be achieved. Figures 4 and 5 show two different volunteers’ data, comparing three b-values using MSND without/with macroscopic motion correction. The proposed motion correction can improve image quality for water, fat, and ADC quantification simultaneously.

Discussion and conclusion

The proposed method allows for good correction of both macroscopic and physiological motion in DW multi-shot EPI to estimate artifact-free water/fat images with ADC maps. Future studies will include experiments in other anatomies such as the head/neck, breast and abdomen where good fat suppression is also required, and unavoidable macroscopic motion is present.

Acknowledgements

The authors would like to acknowledge NWO-TTW (HTSM-17104).