1012
Motion-Compensated Slice-by-Slice ∆B0 Shimming with an AC/DC Shim Coil and Dual-Echo vNavs1Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 3Department of Radiology, Harvard Medical School, Boston, MA, United States
Synopsis
Keywords: Motion Correction, fMRI
Subject motion results in intra-scan ∆B0 changes which are uncompensated in conventional ∆B0 shimming methods. Rapidly switchable shim currents and ∆B0 vNavigators together enable motion-compensated shimming. We have demonstrated successful measurement, calculation, and application of motion-compensated slice-by-slice shims using and AC/DC coil and vNav ∆B0 maps. Motion-compensated slice-by-slice homogeneity shimming improves shim robustness to subject motion and enables compatibility with changing slice prescriptions of prospective motion correction.Introduction
Subject induced ∆B0 inhomogeneity caused by magnetic susceptibility discontinuities in the subject deteriorates image quality in key regions in brain imaging. Shim systems, ranging from scanner-integrated second order spherical harmonic arrays (2-SH) to local shim arrays, improve image quality by canceling subject-induced field perturbations. Rapidly-switchable shim systems, such as the AC/DC shim coil, enable further performance improvements in slice-based imaging by tailoring shim fields on a slice-by-slice basis.Conventionally, shimming procedures are performed at the beginning of an exam, and optionally before each scan. However, over the course of a scan, subject motion invalidates the shim volume. Furthermore, rotation about either axis perpendicular to B0 will change the subject induced ∆B0 field.
In recent work, we demonstrated motion-compensated whole-brain AC/DC shimming [1] via low resolution 2-TE 3D EPI vNavs [2, 3]. This work expands previous capability by performing motion-compensated slice-by-slice (SBS) AC/DC shimming of 2D EPI, based on estimates of the changing ∆B0 field provided by vNavs acquired in each TR.
Methods
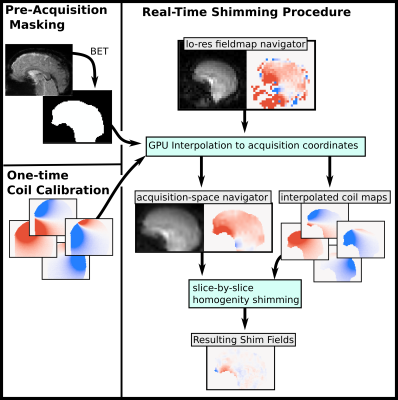
Proposed motion-compensated SBS shimming is performed as shown in Figure 1. The parent EPI sequence is also prospectively motion corrected based on the vNavs. Each TR, a 2-TE fieldmap vNav is used for prospective motion correction. The navigator and pre-measured coil calibration fields are interpolated into the next acquisition's coordinate system, masked by a pre-acquired, BET computed mask [4]. Slice-by-Slice shim current calculation is posed as a linearly constrained quadratic optimization problem, solved with OSQP [5]. Shim current calculation for all parent EPI slices takes 200 ms each TR.The motion-compensation shimmed EPI sequence is shown in Figure 2. A 2-TE 3D EPI vNav (8 mm iso, 32x32x32 matrix, TE1=6.2ms, TE2 =8.6ms, TR =16ms.) and a calculation delay execute prior to each TR of the motion-corrected parent 2D EPI (2.5 mm iso, 78x78 matrix, 60 slices, TE=30ms, TR=6.2s). Triggers from the scanner signal the change between slice-specific shim currents before slice excitation. Currents are zeroed after the EPI readout and during the EPI vNav.
In vivo motion shimming experiments were conducted in one human subject on a 3T Prisma scanner. Experiments were performed using a 32 channel AC/DC integrated RfRx ∆B0 shim array [6] with a 32 channel shim amplifier [7]. During motion-compensation shimmed EPI, the subject was instructed to move to and hold a series of poses for 9 TRs. Shim settings alternated between static whole-brain (WB) second order spherical harmonic (2-SH), static SBS AC/DC, and motion-compensated (MC) SBS AC/DC states. In each pose, successive EPI volumes were obtained with all shim options. Static WB AC/DC shim currents were computed for reference.
Static WB 2-SH shim settings were set via scanner adjustments. Static SBS AC/DC currents were set via offline shim optimization from a 2-echo 2D-GRE field map (110x110 matrix 75 slice, 2.5 mm iso) acquired preceding motion experiments.
Results
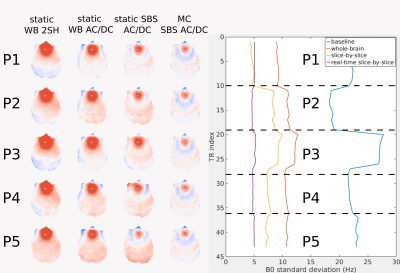
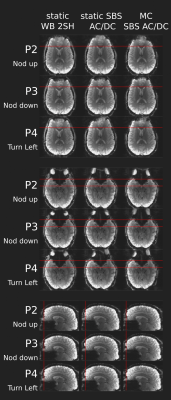
Predicted ∆B0 fields under each shim condition are computed by adding predicted shim fields to the interpolated vNav fieldmaps. Predicted fields from the static WB 2-SH, static WB AC/DC, static SBS AC/DC, and motion-compensated SBS AC/DC shims are shown for each pose in Figure 3. Effective-whole-brain ∆B0 standard deviation is shown as a function of the TR index. Partial-voxel and large-voxel effects from the vNav bias the computed predicted ∆B0. Thus, ∆B0 summary statistics may not be compared to ∆B0 statistics from high-res acquisitions, but provide useful relative reference. Static SBS AC/DC shim outperforms the motion-compensated shim in pose-1; the static shim currents were computed in pose-1 from high resolution field maps. In all other poses, including the return to the neutral pose, the proposed motion-compensated SBS AC/DC shim outperforms other shim conditions.2D EPI motion study magnitude images are shown in Figure 4. For each shim condition, the animated Figure alternates between pose-1 and subsequent poses to demonstrate change in distortion. Motion-compensated SBS AC/DC shimming shows the lowest change in image distortion demonstrating the success of the method. However, motion-compensated shimming shows an increase in dephasing due to poor estimates of z-directed ∆B0 gradients as a result of the large vNav voxels.
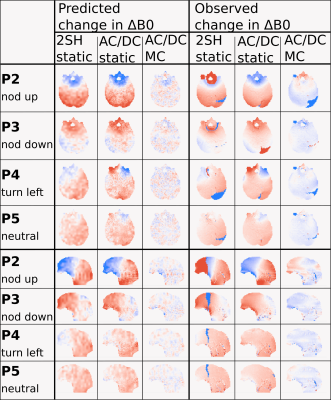
We validate predicted shimmed ∆B0 maps by examining phase data from the parent EPI. Though single echo EPI phase does not provide absolute ∆B0, we observe ∆B0 changes from TR-to-TR via phase differences. Figure 5 shows predicted and observed change in ∆B0 between each pose and pose-1. We find close agreement between predicted and observed fields showing the effectiveness of the motion-compensated shim method.
Discussion
We have demonstrated successful measurement, calculation, and application of motion-compensated slice-by-slice shims using and AC/DC coil and vNav ∆B0 maps. Motion-compensated slice-by-slice homogeneity shimming improves shim robustness to subject motion and enables compatibility with changing slice prescriptions of prospective motion correction. Anatomical consistency of EPI was improved with motion-compensated shimming over static comparisons in nodding and rotating poses. However, motion-compensated SBS shimming caused slight increase in signal dephasing, counter to what is observed in static SBS shimming studies. vNav resolution may limit estimation of large ∆B0 gradients and thus limit shimming’s mitigation of dephasing. Accelerated 2TE vNavs for reduced distortion and increased resolution may further improve the effectiveness of this motion-compensated SBS Homogeneity shimming method.Acknowledgements
The authors the following funding sources: NIH R01CA255479l NIH R01HD085813, R01HD03578, R01EB028797, R01HD099846, R21EB029641.
We acknowledge the engineering work of Dylan Tisdall and Aaron Hess who contributed to
the 2TE vNav infrastructure used in this study, Thomas Witzel for contributions to real-time shimming and scanner interfacing, and Danny Park and Jon Polimeni for providing the EPI
sequence.
References
[1] N Arango, R Frost, P Wighton, J Stockmann, O Andronesi, and A van der Kouwe. Real-time motion compensated B0 shimming with an AC/DC shim coil and dual-echo vNavs. ISMRM, 856, 2022.
[2] Aaron T Hess, M Dylan Tisdall, Ovidiu C Andronesi, Ernesta M Meintjes, and André JW van der Kouwe. Real-time motion and b0 corrected single voxel spectroscopy using volumetric navigators. Magnetic resonance in medicine, 66(2):314–323, 2011.
[3] Aaron T Hess, Ovidiu C Andronesi, M Dylan Tisdall, A Gregory Sorensen, André JW van der Kouwe, and Ernesta M Meintjes. Real-time motion and b0 correction for localized adiabatic selective refocusing (laser) mrsi using echo planar imaging volumetric navigators. NMR in Biomedicine, 25(2):347–358, 2012.
[4] Stephen M Smith. Bet: Brain extraction tool. FMRIB TR00SMS2b, Oxford Centre for Functional Magnetic Resonance Imaging of the Brain), Department of Clinical Neurology, Oxford University, John Radcliffe Hospital, Headington, UK, 2000.
[5] B. Stellato, G. Banjac, P. Goulart, A. Bemporad, and S. Boyd. OSQP: an operator splitting solver for quadratic programs. Mathematical Programming Computation, 12(4):637–672, 2020.
[6] Jason P Stockmann, Thomas Witzel, Boris Keil, Jonathan R Polimeni, Azma Mareyam, Cristen LaPierre, Kawin Setsompop, and Lawrence L Wald. A 32-channel combined rf and b0 shim array for 3t brain imaging. Magnetic resonance in medicine, 75(1):441–451, 2016.
[7] N Arango, J Stockmann, T Witzel, L Wald, and J. White. Open-source acquisition-speed slice-by-slice controller for 32 coil b0 shimming. ISMRM, 2682, 2017.
Figures